Fluid Mechanics 3(2+1)

Lesson-17: CONTINUITY EQUATION

17.1 Principle of conservation of mass

Let us consider a material volume V with bounding surface S. The principle of conservation of mass imposes that: the material derivative of the mass of fluid in V is equal to zero.

The mass of the fluid in V is given by

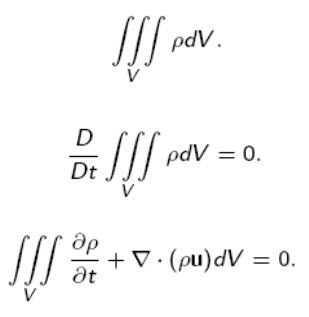
since the volume V is arbitrary the following differential equation holds

This equation is known in fluid mechanics as continuity equation.

In the particular case in which the fluid is incompressible, i.e. the density ρ is constant, the above equation reduces to

This implies that the velocity field of an incompressible fluid is divergence free.

17.2 CONTINUITY EQUATION

Rate of flow or discharge (Q) is the volume of fluid flowing per second. For incompressible fluids flowing across a section,

Volume flow rate,

 Q= AV m³/s

where

A=cross sectional area and

V= average velocity.

For compressible fluids, rate of flow is expressed as mass of fluid flowing across a section per second.

Mass flow rate (m) =(ρAV) kg/s where ρ = density.

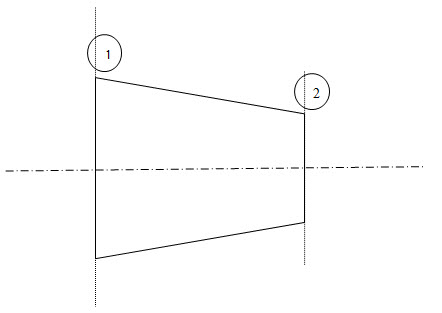
Continuity equation is based on Law of Conservation of Mass. For a fluid flowing through a pipe, in a steady flow, the quantity of fluid flowing per second at all cross-sections is a constant.

Let v₁=average velocity at section [1],

r₁=density of fluid at [1], A₁=area of flow at [1];

Let v₂, r₂, A₂ be corresponding values at section [2].

Rate of flow at section [1]= r₁ A₁ v₁

Rate of flow at section [2]= r₂ A₂ v₂

r₁ A₁ v₁= r₂ A₂ v₂

This equation is applicable to steady compressible or incompressible fluid flows and is called Continuity Equation.

If the fluid is incompressible, r₁ = r₂ and the continuity equation reduces to A₁ v₁= A₂ v₂

For steady, one dimensional flow with one inlet and one outlet:

r₁ A₁ v₁ - r₂ A₂v₂=0

For control volume with N inlets and outlets

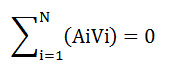
where inflows are positive and outflows are negative .

Velocities are normal to the areas. This is the continuity equation for steady one dimensional flow through a fixed control volume

When density is constant,

17.3 Momentum equation in integral form

Let us consider a material volume V with bounding surface S. Newton’s first principle states that: the material derivative of the momentum of the fluid in V is equal to the resultant of all external forces acting on the volume.

The momentum of the fluid in V is given by:

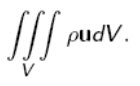
Therefore we have (in index notation):

This is the integral form of the momentum equation and is often written in compact form as:

I +W = F + ∑,

with I named local inertia and W being the flux of momentum across S.