Fluid Mechanics 3(2+1)

LESSON 24. LAMINAR AND TURBULENT FLOW

In turbulent flow the streak-lines show wiggles and vortices. The fluid does not flow smoothly down the pipe.

What happens when fluid enters a pipe?

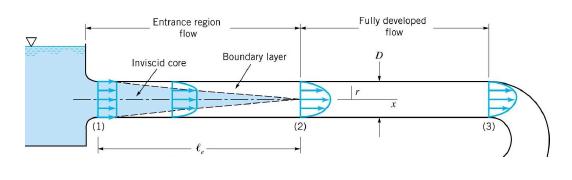
The fluid adjacent to the wall sticks to the wall due to friction effects. This is the no-slip condition and occurs for all liquids.

• This boundary layer grows until it reaches all parts of the pipe.

• Inside the inviscid core, viscosity effects are not important.

• The entrance region for laminar flow is given by

Past here the flow is fully developed.

Laminar flow analysis

Assumptions, outside entrance region:

And steady flow. Horizontal flow

 

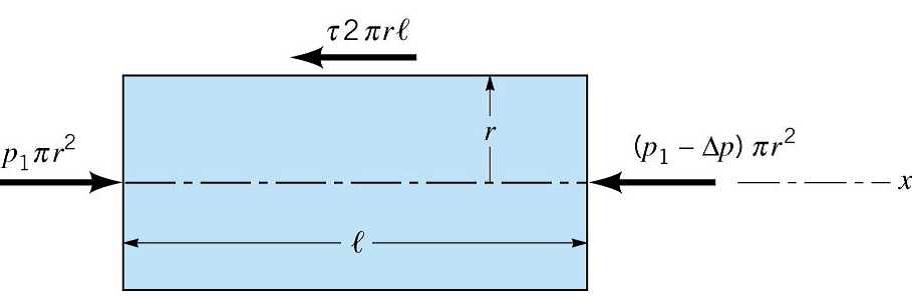
Apply F = ma to a cylinder.

The cylinder becomes distorted as t → t + ∂t

• The pressure is constant along the vertical direction.

• The pressure along horizontal direction does change. Δp = p2 − p1 < 0

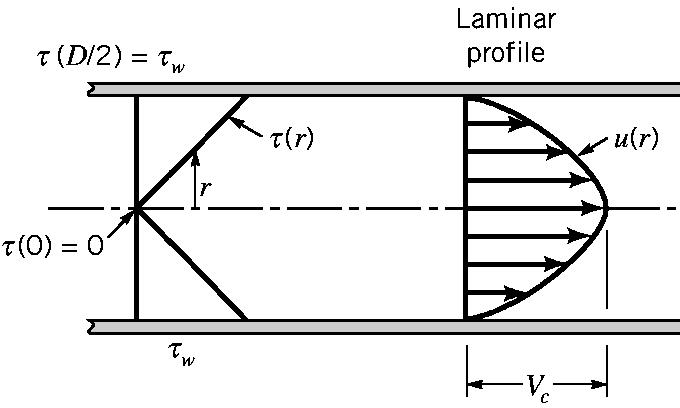
• There is a viscous shear stress acting along the surface cylinder and The shear stress is a function of the radius of the cylinder.

Application of F = ma

 

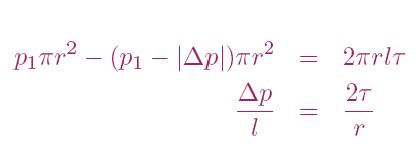
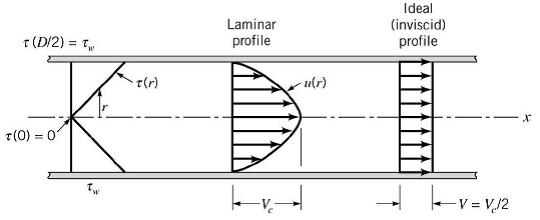
The shear stress is largest at the walls

Laminar velocity profile

To determine the laminar velocity profile, assume we have a Newtonian fluid, so

The flow rate is parabolic, with largest velocity in  middle of pipe and zero velocity at wall.

 

Laminar flow rate

Just need to integrate the laminar velocity profile over the cross sectional area. Divide cross section into thin annular strips

 

Pouiseuille’s Law and Interpretation

The fundamental result

 

is usually called Poiseuille’s Law. Laminar flow in pipes is sometimes termed Hagen-Poiseuille’s flow.

Flow along a pipe is driven by a pressure difference.

The viscosity acts to retard the passage of the fluid along the pipe through the no-slip condition at the wall. The flow rate