Site pages
Current course
Participants
General
MODULE 1. FLUIDS MECHANICS
MODULE 2. PROPERTIES OF FLUIDS
MODULE 3. PRESSURE AND ITS MEASUREMENT
MODULE 4. PASCAL’S LAW
MODULE 5. PRESSURE FORCES ON PLANE AND CURVED SUR...
MODULE 6.
MODULE 7. BUOYANCY, METACENTRE AND METACENTRIC HEI...
MODULE 8. KINEMATICS OF FLUID FLOW
MODULE 9: CIRCULATION AND VORTICITY
MODULE 10.
MODULE 11.
MODULE 12, 13. FLUID DYNAMICS
MODULE 14.
MODULE 15. LAMINAR AND TURBULENT FLOW IN PIPES
MODULE 16. GENERAL EQUATION FOR HEAD LOSS-DARCY EQ...
MODULE 17.
MODULE 18. MAJOR AND MINOR HYDRAULIC LOSSES THROUG...
MODULE 19.
MODULE 20.
MODULE 21. DIMENSIONAL ANALYSIS AND SIMILITUDE
MODULE 22. INTRODUCTION TO FLUID MACHINERY
LESSON 27. MAJOR AND MINOR HYDRAULIC LOSSES THROUGH PIPES AND FITTING
LOSSES IN PIPE FLOW
-
The flow through most pipes is turbulent. Treatment with classical analytic techniques next to impossible. Available techniques are basic on experimental data and empirical formulae. The working equations are often derived from dimensional analysis using dimensionless forms. Often desirable to determine the head loss, hL so that the energy equation can be used. Pipe systems come with valves, bends, pipe diameter changes, elbows which also contribute to the energy (head) loss.
-
The overall head loss is divided into two parts major loss hLmajor , and minor loss hLminor . The major loss comes from viscosity (in straight pipe) while the minor loss is due to energy loss in the components.
-
The major loss can actually be smaller than the minor loss for a pipe system containing short pipes and many bends and valves.
-
When a fluid flows through a pipe, there is some resistance to fluid due to which fluid loses itsenergy. This loss of energy can be classified in to following types.
-
It is often necessary to determine the head loss, hL, that occur in a pipe flow so that the energy equation, can be used in the analysis of pipe flow problems.
-
The overall head loss for the pipe system consists of the head loss due to viscous effects in the straight pipes, termed the major loss and denoted hL-major.
-
The head loss in various pipe components, termed the minor loss and denoted hL-minor.
hL = hL-major + hL-minor
For a pipe system that contains many components and a relatively short length of pipe, the minor loss may actually be larger than the major loss.
Major Losses
Darcy-Weisbach formula
The head loss, hL-major is given as ;
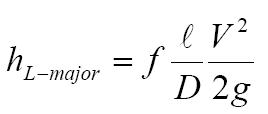
where f is friction factor.
- It is valid for any fully developed, steady, incompressible pipe flow, whether the pipe is horizontal or on hill.
Friction factor for laminar flow is
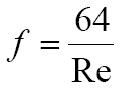
- Friction factor for turbulent flow is based on Moody chart.
It is because, in turbulent flow, Reynolds number and relative roughness influence the friction.
- Reynolds number is given by following,
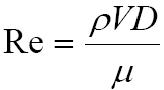
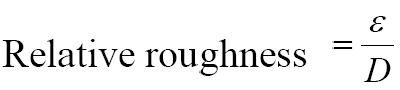
(relative roughness is not present in the laminar flow)
The pressure loss in a pipe for turbulent flow:
-
Depends on the following
• ρ
• μ
-
v , l and D
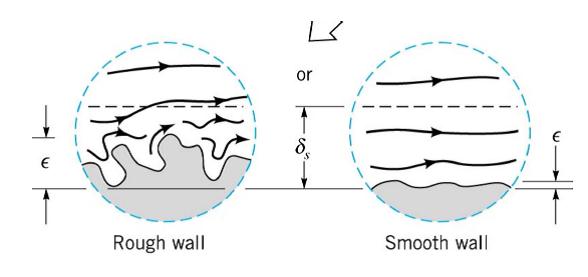
- Surface roughness ε.
These projections of the wall can and protrude out of the laminar sub-layer.
Viscous flows in pipes
Generalized one-dimensional Bernoulli equation for viscous flow.
When the viscosity of the fluid is taken into account total energy head
![]()
Is no longer constant along the pipe. In direction of flow, due to friction cause by viscosity of the fluid we have
![]()
So to restore the equality we must add some scalar quantity to the right side of this inequality
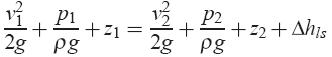
This scalar quantity Dhls is called as hydraulic loss. The hydraulic loss between two different cross section along the pipe is equal to the difference of total energy for this cross section:
![]()
We must remember that always H1 > H2. In horizontal pipe when z1 = z2 and diameter of pipe is constant v1 = v2 hydraulic loss is equal to the head of pressure drop or head loss
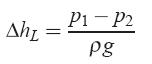
Head loss is express by Darcy -Weisbach equation:
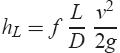
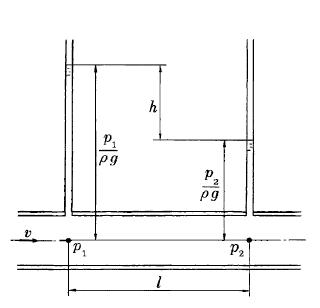
Figure 1: Pipe friction loss. For horizontal pipe, with constant diameter this loss may be measured by height of the pressure drop: Δp/ρg = h
We must remember that equation (4) is valid only for horizontal pipes. In general, with v1 = v2
but z1 ≠ z2, the head loss is given
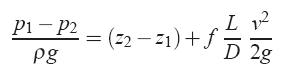
Part of the pressure change is due to elevation change and part is due to head loss associated with frictional effects, which are given in terms of the friction factor f that depends on Reynolds number and relative roughness
![]()