Soil & Water Conservation Engg.

Lesson 21 In-stream Sediment Measurements

21.1 Location of Measurement

When the question ‘where to measure’ comes to our mind the most obvious answer in a broader sense is where the data can be collected, however the answer is not so simple. It becomes quiet complex when sediment concentrations or loads of an entire large area need to be characterized which largely depends on the information wanted and the particular situation being studied. Generally, measurements should be made downstream as close as possible to the area of disturbance. The effect of a sediment-producing condition is attenuated and its effect is confounded with the effects of dilution and other sediment sources farther downstream. If the downstream effects of a disturbance are being studied, it is better to measure at the affected site.

The location of measuring station also depends on the hydraulic conditions in the stream. In some streams, control can be affected by geology or large organic debris. Bedrock cropping out at the crest of major riffles or falls can provide excellent control in natural channels. In some situations, well emplaced logs stabilize the channels and provide suitable locations to measure both the suspended sediment concentration and discharge. Along with location, depth is the other factor which affects the concentration of sediment in the streams i.e. near the stream bed it is more, in the middle relatively less, while on the top of the surface it is too less. Thus it is very difficult to select the sampling point, which can accurately define the sediment concentration in vertical cross-section of stream.

21.2 Frequency of Measurement

Frequency of sampling depends upon the sediment concentration in the stream flow. It is well known that the sediment concentration increases rapidly on the rising phase of the hydrograph than the falling phase. Therefore, sediment samples should be collected more frequently at the beginning of runoff and it should be continued up to the peak stage of runoff. The sample should be taken at every 15 minutes interval.

21.3 Number of Monitoring Stations

In most of the cases the entire runoff of the watershed is drained from a single point known as the outlet, the collection of the sediment sample should be carried out from the outlet point.  The outlet is an ideal location of monitoring station for the entire watershed. Similarly, in case of drainage system, where flow is drained from more than one points, gauging station should be provided at each outlet point for sampling.

21.4 Observation and Collection of Sediment Samples

There are several methods which are used today for evaluation of sediment transport in rivers. The total number of sampling points (Table 21.1) to be considered for collecting the sediment samples depends on the width of the stream flow.

Table 21.1. Number of Sampling Points in the Stream.

Width of Stream (m)	No. of Sampling Points	Location of Point from Site
< 30	3	25, 50 and 75% of the stream width
30 - 300	5	25, 35, 50, 65 and 80% of the stream width
> 300	7	15, 30, 40, 50, 60,70 and 85% of the stream width

 

Apart from width-wise sediment sampling, the depth-wise sampling is also carried out using the following points:

1. In case of single point sampling, the sample should be collected from the depth of 0.6 d, measured from the surface (d = the depth of the stream).

2. In case of double point sampling, one sample should be collected from the point near the top of water surface i.e. at a depth of about 0.2 d and other near the stream bed at about 0.8 d. The concentration of sediment is weighted equally.

3. For three point sampling: one sample should be taken near the top of water surface, second from mid depth of stream and the third near the stream bed, and weighted equally.

4. Similarly, in case of multiple sampling, there should be several samples from several points of vertical section of the stream flow. This helps to elaborate the sediment distribution in the stream.

5. The sediment sampler should be kept in vertical position from the stream bed.

6. The mouth of the sampler should be opened after reaching the desired depth of stream flow.

7. Whenever it is expected that the distribution of sediment is uniform in the stream flow, sampling should be done only at 0.6d of the stream flow.

21.5 Estimation of Different Loads from Samples

Bed load is not amenable to theoretical treatment. The following two methods are generally used for estimation of bed load.

1. Analytical Method

2. Stream Sampling

1. Analytical Method:  Computation of bed-load movement using analytical method involves several relations; these relations can be empirical or analytical. The derivation of the relation is done based on the following two basic concepts:

1) A minimum fluid force is exerted on the soil particles before initiating their movement.   

2) The force exerted by the soil particles on the channel bed is not constant, but varies about some mean value. This concept is based on the theory of turbulent flow.

The different forces acting on the soil particles of non-cohesive material are basically the gravity and fluid forces. The analytical method for computing the bed load transport involves several empirical relations. Few of them are described as under:

Du Boys Formula: This formula is based on the theory of tractive force, which was derived on the assumptions that the coarser particles are moved in the form of layers and subject to uniform tractive force and vertical velocity gradient of the moving coarser particles is linear. The formula for bed load estimation is written as under:

where, q_s = rate of bed load transport (volume per second per unit stream width); c_s = coefficient, depends upon the shape and size of the sediment particle = 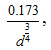, where d is the grain diameter (mm); T₀ = average shear stress exerted on the channel boundary and T_c = critical shear stress.

An estimate of the average boundary shear stress (T₀) exerted by the fluid on the bed is:

where, γ = the specific weight of water, D = the flow depth (~ hydraulic radius), and S_f  = the friction slope.

And the estimate of Critical shear stress () can be defined by equating the applied forces to the resisting forces. For soil grains of diameter d and angle of repose  on a flat bed, the following relations can approximate the critical shear for various sizes of sediment:

For clays,

For silts and sands,

For gravels and cobbles,

where,

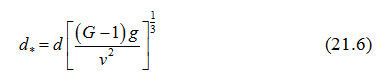
And = the unit weight of the sediment; = the unit weight of the water/sediment mixture; G = the specific gravity of the sediment; g = gravitational acceleration; v = the kinematic viscosity of the water/sediment mixture

Shield’s Formula: Shield's formula is applied for estimating the bed load movement consisting of uniform size of sediments. The equation was derived by considering the effect of specific gravity of the sediment. The Shield's formula is written as:

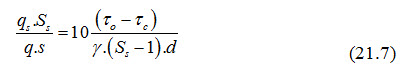
where, S_s = specific gravity of sediments, such as stone grains; S = stream bed slope (mm); q_s = discharge rate (m³/s per unit width of stream); q = discharge per unit channel width;  = specific gravity of the fluid; d = diameter of sediment (mm).

Mayer Peter’s Formula: This was developed based on the effect of grain diameter, slope of channel bed and discharge characteristics of flow on bed load movement. It is written as:

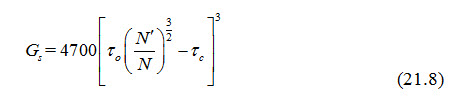
where, G_s = rate of bed load transport per unit width of channel (kg/h.m);  = Mannning’s roughness coefficient for plain bed = ,  in which d is the effective grain diameter; N = actual value of Manning's roughness coefficient for rippled bed. Generally, the value of N is taken as 0.020 for discharge of more than 11 m³/s and 0.0225 for a lower discharge value; = unit tractive force exerted by flowing water = 0.97·. RS;  = critical shear stress required to displace the sediments = 0.07 d, kg/m²; R = hydraulic mean depth and S = stream bed slope.

Chang Formula: Chang proposed the following formula for estimating the bed load:

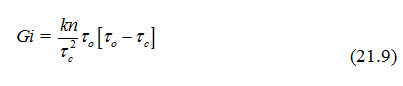
where, Gi = rate of bed-load transport in pounds/second/unit width; k =  constant; n  = Manning's roughness coefficient; = unit tractive force due to stream water flow,  = critical shear stress required to displace the sediment = 0.0175 (1.65 d)^x when specific gravity of the sediment is 2.65; in which, d is sediment diameter (mm); x = exponent which is either equal to unit or half, depending upon whether  the value of 1.65 d is greater or less than unity respectively.

Schoklitsch Formula: This formula was developed based on experimental data, obtained by installation of flume in the stream. The Schoklitsch formula assumes that the bed-load contains the materials of uniform size.

The formula may be written as:

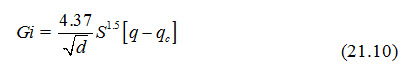
where, Gi = rate of bed-load transport (F.P.s) (kg/s); d = particle diameter (m); S = slope of stream bed; q = observed discharge (m³/s); q_c =  critical discharge (m³/s); it is given by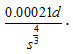

2. Stream Sampling [Bed Load Sampling]

The estimation of rate of bed load movement through the stream flow is carried out by placing the sampler over the bed and measuring the amount of materials collected for a given time. The samplers used for collecting the bed load sample are known as bed load samplers. The sampler is kept in position by a rod, when the depth of stream flow is low or by a cable from the boat, from a trolley or pulley running on a cable spanned across the river or from a bridge. The lowering and raising of the sampler is done with the help of a winch. Based on the construction and principles of operation, bed-load samplers are of different types. They are:  

1. Basket Type

2. Tray or Pan Type

3. Pressure Difference Type

For estimating the bed load, the samples collected through the samplers are dried and weighted. The dry weight is then divided by the time taken for measurement and width of the stream bed to get the bed load movement per unit stream width per unit time. A curve between the rate of movement and stream flow can also be drawn. From this rating curve, the rate of bed load movement for different discharges of the stream can be determined. This is usually practiced as continuous discharge measurement using stage level recorder is much easier compared to continuous monitoring of bed load.

Bed load is the sum of saltation load and surface creep. It is obtained either by using bed load samplers or can be computed by using several formulae. In case, the measurement of bed load is not possible due to some unforeseen reasons, then depending upon bed load materials, an amount ranging from 2.5% to 15% of suspended load is added to the suspended load as bed load to get the amount of sediment load transported by stream flow.

Keywords: In-stream Sediment Measurements, Analytical Methods, Stream Sampling, Pressure Difference Type, Mayer Peter’s Formula.

References

Suresh, R. (2009). Soil and Water Conservation Engineering, Standard Publishers Distributors, 951 p.

Thomas, R. B. (1985). Measuring Suspended Sediment in Small Mountain Streams, Pacific Southwest Forest and Range Experiment Station P.O. Box 245, Berkeley, California 94701.

Suggested Readings

http://mi.water.usgs.gov/pdf/sedimentpaper.pdf

http://water.usgs.gov/osw/techniques/Gray_Simoes.pdf

http://www.who.int/water_sanitation_health/resourcesquality/wqmchap13.pdf