Strength of Material

LESSON 19. Displacement Method: Moment Distribution Method – 5

Example 1

Draw the bending moment diagram for the follwing frame. EI is constant for all members.

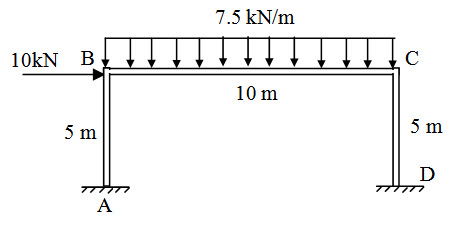
Fig. 19.1.

The above problem can be represented as the superposition of two sub-problems as shwon in Figure 18.2.

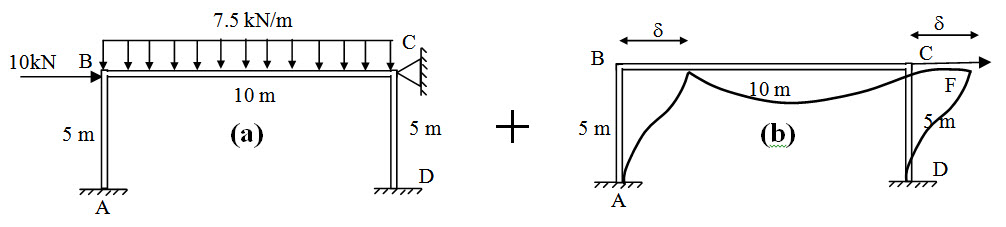Fig. 19.2.

In the first sub-problem (Figure 18.2a), sidesway is prevented and therefore can be analyzed by moment distribtuin mehod as discussed in the previous lesson. Suppose C_x be the horizontal reaction at C. Now in the second sub-problem apply an arbitrary sidesway d as shown in Figure 18.2b. Calculate horizontal force F due to arbitrary sidesway d. Then the beam end moment in the orizinal structure is obtained as,

\[M{}_{original} = M{}_{sub - problem1} + kM{}_{sub - problem2}\]

Where, \[k={{{C_x}} \over F}\]

Step1: Solution of sub-problem 1 (sidesway restrained)

\[{k_{BA}}={{4E{I_{BA}}} \over {{L_{BA}}}}={{4EI} \over 5}\] ,  \[{k_{BC}}={{4E{I_{BC}}} \over {{L_{BC}}}}={{2EI} \over 5}\]  and  \[{k_{CD}}={{4E{I_{CD}}} \over {{L_{CD}}}} = {{4EI} \over 5}\]

Distribution factors are,

\[D{F_{BA}}={2 \over 3}\] ,  \[D{F_{BC}}={1 \over 3}\] ,  \[D{F_{CB}}={1 \over 3}\]  and  \[D{F_{CD}}={2 \over 3}\]

End A is fixed and therefore no moment will be carrid over to B from A. Carry over factors for other joints,

\[C_{BA}={1 \over 2}\] ,  \[C_{BC}={1 \over 2}\] ,  \[C_{CB}={1 \over 2}\]  and  \[C_{CD}={1 \over 2}\]

Fixed end moments are,
\[M{}_{FBC}=-{{7.5 \times {{10}^2}} \over {12}}=-62.5{\rm{kNm}}\] ;   \[M{}_{FCB}=-{{7.5 \times {{10}^2}} \over {12}}=62.5{\rm{kNm}}\]

\[M{}_{FAB} = M{}_{FBA} = M{}_{FCD} = M{}_{FDC}=0\]

Calculations are performed in the following Table.

 

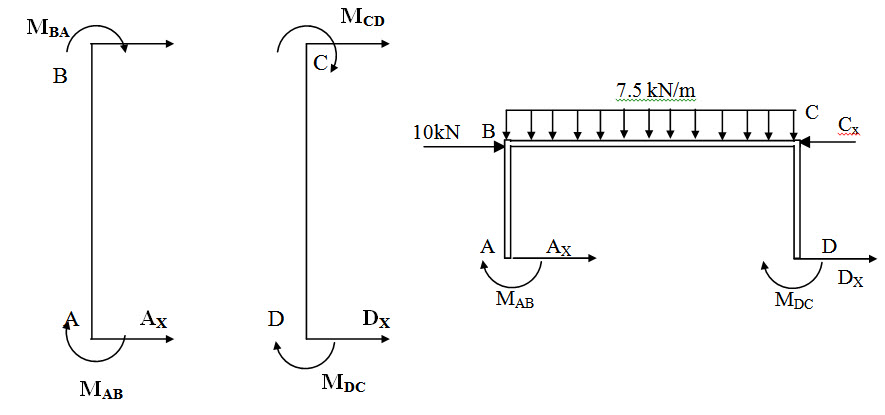
Fig. 19.3.

From the free body diagram of AB and CD (Figure 18.3),

\[{A_x}={{{M_{AB}} + {M_{BA}}} \over {{L_{AB}}}}={{25 + 50} \over 5}=75{\rm{ kN}}\]

\[{D_x}={{{M_{CD}} + {M_{DC}}} \over {{L_{CD}}}}={{ - 25 - 50} \over 5}=75{\rm{ kN}}\]

Also,

\[{C_x}=10 + {A_x} + {B_x}=10{\rm{ - 75}} + 7{\rm{5}}={\rm{1}}0{\rm{ kN}}\]

Step 2: Solution of sub-problem 2 (for an arbitrary sidesway)

Let an arbitray sway δ = 100 / EI is applied at C. Fixed end moments due to δ are,

\[M{}_{FAB}=M{}_{FBA}=-{{6EI\delta } \over {{L_{AB}}}}=-{{6EI} \over 5} \times {{100} \over {EI}}=-120{\rm{ kNm}}\]

\[M{}_{FCD}=M{}_{FDC}=-{{6EI\delta } \over {{L_{CD}}}}=-{{6EI} \over 5} \times {{100} \over {EI}}=-120{\rm{ kNm}}\]

Moment distribution calculations,

Horizontal reactions at A and D are,

\[{A_x}={{{M_{AB}} + {M_{BA}}} \over {{L_{AB}}}}={{ - 85.75 - 51.45} \over 5}=-27.44{\rm{ kN}}\]

\[{D_x}={{{M_{CD}} + {M_{DC}}} \over {{L_{CD}}}}={{ - 85.75 - 51.45} \over 5}=-27.44{\rm{ kN}}\]

Therefore, total horizontal force due to lateral sway δ = 100 / EI  an be ditermined by the following equilibrium equation,

\[F + {A_x} + {D_x}=0 \Rightarrow F = 54.88{\rm{ kN}}\]

Hence, \[k = {C_x}/F=10/54.88\]

Final moment now can be obtained as,

\[M{}_{original}=M{}_{sub - problem1} + kM{}_{sub - problem2}\]

Therefore,

\[M{}_{AB} = M{}_{AB1} + kM{}_{AB2}=25 + \left( {10/54.88} \right) \times ( - 85.75) = 9.375{\rm{ kNm}}\]

\[M{}_{BA} = M{}_{BA1} + kM{}_{BA2}=50 + \left( {10/54.88} \right) \times ( - 51.45)=40.625{\rm{ kNm}}\]

\[M{}_{BC}=M{}_{BC1} + kM{}_{BC2}=-50 + \left( {10/54.88} \right) \times (51.45)=-40.625{\rm{ kNm}}\]

\[M{}_{CB}=M{}_{CB1} + kM{}_{CB2}=50 + \left( {10/54.88} \right) \times (51.45)=59.375{\rm{ kNm}}\]

\[M{}_{CD}=M{}_{CD1} + kM{}_{CD2}=-50 + \left( {10/54.88} \right) \times ( - 51.45)=-59.375{\rm{ kNm}}\]

\[M{}_{DC}=M{}_{DC1} + kM{}_{DC2}=-25 + \left( {10/54.88} \right) \times ( - 85.75)=-40.625{\rm{ kNm}}\]

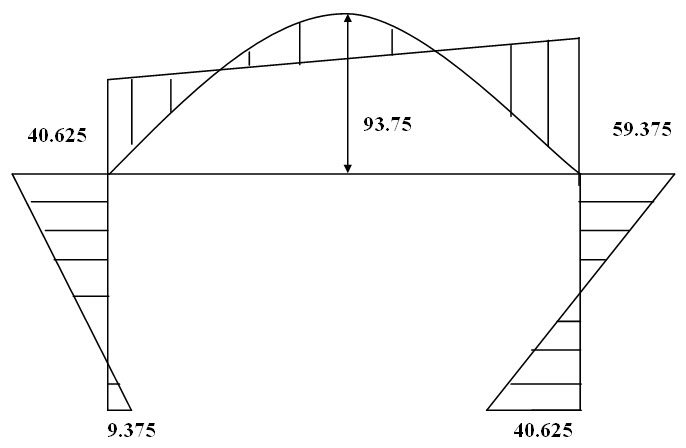
Figure 19.4: Bending moment Diagram.

 

Suggested Readings

Hbbeler, R. C. (2002). Structural Analysis, Pearson Education (Singapore) Pte. Ltd.,Delhi.

Jain, A.K., Punmia, B.C., Jain, A.K., (2004). Theory of Structures. Twelfth Edition, Laxmi Publications. 

Menon, D.,  (2008), Structural Analysis, Narosa Publishing House Pvt. Ltd., New Delhi.

Hsieh, Y.Y., (1987), Elementry Theory of Structures , Third Ddition, Prentrice Hall.