Site pages
Current course
Participants
General
Module 1. Tractor Mechanics
Module 2. Traction
Module 3. Introduction to Transmission System
Module 4. Clutch System
Module 5. Gear Box
Module 6. Differential and Final drive
Module 7. Brakes
Module 8. Steering system
Module 9. Hydraulics
Module 10. Power Transmission
Lesson 21. Calculation of braking effort.
Weight Transfer:
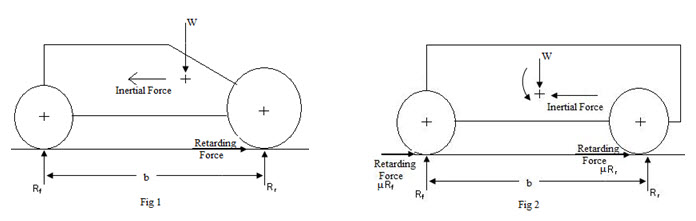
The figure 2 shows a body moving towards the left with an inertial force. Brake is applied, which produces a retarding force at the road surface. This retarding force at the road surface causes an overturning couple on the body due to which weight transfer takes place from the rear to the front wheels.
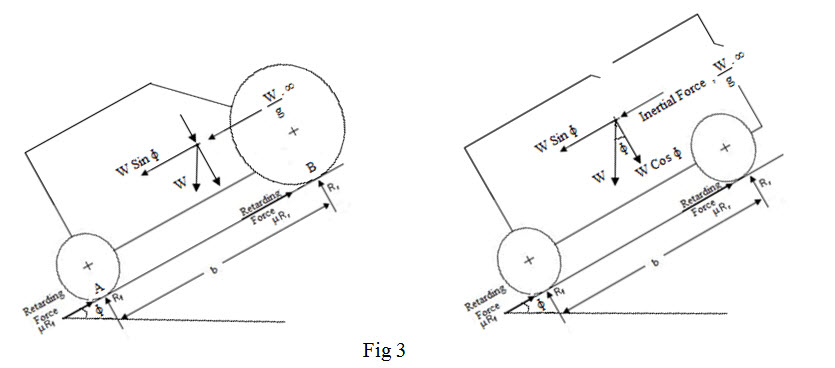
In figure 3, the body is coming down a gradient of angle f when the brakes are applied.
W = Weight of the vehicle
Rf= Normal reaction on the front wheel
Rr= Normal reaction on the rear wheel
b = Wheelbase
h = Height of CG from the surface of the road
∞ = Retarding force due to breaking
μ = Coefficient of friction between the wheels and the road surface
μRf= Braking force on the front wheels
μRr= Braking force on the rear wheels
When brakes are applied on all the wheels
Rf + Rr = W Cos \[\phi \] -1
μRf + μRr = W Sin \[\phi \] + W .∞ -2
g
In case of equilibrium ∑ M=0 at point B
W . ∞.h + W Sin \[\phi \]. h + W Cos \[\phi \]. x - Rf. b
g
From equation 1 and 2
Μ W Cos \[\phi \] = W Sin \[\phi \] + W. ∞
g
∞ = μ.Cos \[\phi \] - Sin \[\phi \] -4
g
From equation 3 and 4
Rf = W(x +μh). Cos \[\phi \]
b
Rr=W(b- x- μh) . Cos \[\phi \]
b
Case of Indian Agricultural Tractors
While most of the automobiles have an all wheel braking but most of the Indian Agricultural Tractors, being rear wheel drive, have braking only in the rear wheels.
The weight transfer in case of tractors with braking in the rear wheels only is analyzed as follows:
Rf + Rr = W Cos \[\phi \] -5
μRr = W Sin \[\phi \] + W . ∞ -6
g
Taking moments above point A
Rr .b + W.h.Sin \[\phi \] + W . ∞. h – W(b-x)Cos \[\phi \] = 0 -7
g
From equation 6 and 7
∞ =μ(b-x) Cos \[\phi \] - Sin \[\phi \]
g (b + μh)
Rf=W.(b-x). Cos \[\phi \]
(b + μh)
Rr = W(x + μh). Cos \[\phi \]
(b + μh)
In case the body (or the tractor) is moving up the slope, the angle of the slope may be taken as negative and the derived expression can be used.