Renewable Energy Sources 3(2+1)

LESSON 26. Hydropower Energy Sources

The other category of energy is potential energy. This is the energy that is stored in a system by virtue of forces between objects that are separated by some distance. If the objects are allowed to move under the influence of the force between them, then work is done as the force displaces the objects from their initial positions, and energy is transferred. A prime example of this is gravitational potential energy. A ball that is dropped from rest at some height above the Earth's surface will begin to accelerate downward as gravity pulls it. As the ball accelerates, gravity is working on it to convert its potential energy into kinetic energy (the ball's height decreases as its velocity increases). If the ball is dropped from a higher altitude, then gravity operates over a greater distance, thereby generating more kinetic energy, i.e. the gravitational potential energy of an object depends upon the height through which an object is allowed to fall.

Gravitational Potential Energy

Newton’s Universal Law of Gravity tells us that the gravitational force between two objects depends upon the inverse of the square of the distance between the objects and is, therefore, not a constant force with displacement. However, if we limit the movements of the objects to small values compared to the total distance between them, then we can consider the force of gravity to be a constant. Objects falling near the surface of the Earth fall into this category. The distance between the center of the Earth and the center of any object near the surface is over 4,000 miles. If we limit the object to fall a distance of less than a mile, then the change in the force of gravity over that distance is less than .05%. Thus, we can take it to be a constant. In this situation, Newton’s Universal Law of Gravity reduces to the expression:

Fgravity = mass x acceleration due to gravity near Earth = mass x 9.80 m/sec2

Since the force is a constant, the potential energy is merely this force multiplied by the distance through which the object falls. If we allow H to be the height through the object will fall, then the potential energy of the object is:

P.E. = Fgravity x H = mass x 9.80 m/sec2 x H

For a hydroelectric dam, the object that is “falling” is water. The mass of the water that is falling is determined by how much volume it occupies. The relationship between the two is given by the formula mass = density x volume. For fresh water, the density is 1 gm/cm3, which is equivalent to 1000 kg/m3. Thus, our formula for the potential energy of a volume of water V that falls through a height H is

P.E. = (9800 J/m4) x VH

where J is the symbol for the unit of energy called the joule.

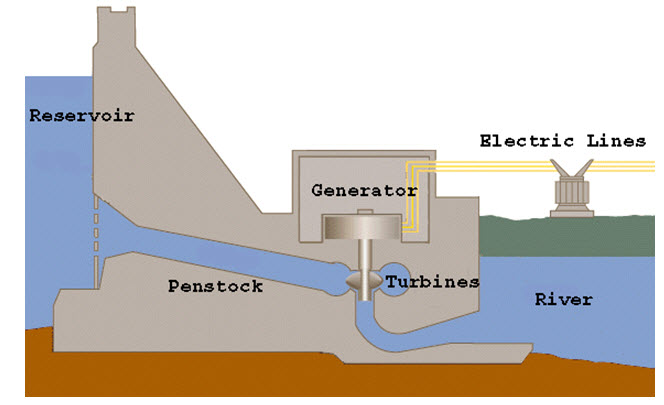
Figure : Diagram of a hydroelectric facility

When we write about the water “falling”, we are giving a somewhat false impression of how a hydroelectric dam works. Figure is a diagram of a conventional hydroelectric facility. As you can see, the water does not fall onto the turbine to turn it. Instead, the water near the bottom of the dam is forced by the pressure of the water above it past the turbines. While this is not the same as falling onto the turbines, it turns out that it is equivalent mathematically. Therefore, the formula that we derived above for potential energy is the one used for a dam, where H is the difference in heights between the surface of the water in the reservoir and the turbine.

Efficiency

This potential energy, though, will not be the actual amount of electrical energy that we can get out of the dam. This is because of the first and second laws of thermodynamics. The first law states that "Energy can neither be created nor destroyed; it can only be transferred from one form to another." While this statement of the first law is the most common expression of it, it really does not say anything about how energy can be transferred. In mathematical terms, the first law is normally stated as

ΔE = W + Q

Where, ΔE is the change in the energy of an object, W is the work done on the object, and Q is the heat added to the object. In laymen's terms, this means that the only way to change the energy of an object is to either do work on it or add heat to it (it should be noted that having the object do work on its surroundings, or allowing the object to give off heat, are equivalent to having negative values for W or Q).

The First Law of Thermodynamics tells us that the energy involved in any transfer must be conserved. This would seem to mean that we should never run out of energy and should pay no heed to anybody talking about an energy crisis. The problem is that this is not the only law that governs energy transfers. While the total amount of energy does not change, the second law of thermodynamics puts limits on the amount of usable energy that can be transferred. One of the consequences of this law is that the total amount of usable energy that comes out of any process will be less than the total amount of energy that went into the process. The difference between the total amount of energy input and the usable energy output is expended as waste heat.

This brings us to the issue of efficiency, which is a measure of the amount of usable energy that is generated during any type of transfer. If a transfer is very efficient, then the amount of usable energy that is generated is almost equal to the total amount of energy that went into the transfer. This means that very little waste energy will be produced. An inefficient transfer, conversely, is one in which most of the energy going into the process is converted to waste heat. For example, a fluorescent light bulb converts about 20% of the electrical energy that runs through it into visible light energy. While this may not sound like a very efficient transfer, it is much better than the 5% efficiency of an incandescent light bulb, which most people use.

When discussing the efficiency of a process, we have to make sure and not forget all of the transfers that might need to take place in order to get to the one under investigation. A great example of this occurs when comparing the efficiencies of electric and internal combustion engine powered cars. The efficiency of the electric motor in a car is about 90%, while the efficiency of the internal combustion engine is only about 25%. However, these efficiencies are not the only things that need to be considered when comparing the two devices. How is the electricity that charges the car created? Where does the gasoline come from that powers the internal combustion engine? What types of transmission systems does each car have? There are many steps and energy transfers that take place in getting each type of car to move, and each one of these has its own individual efficiency. For instance, the average coal burning electric plant is only about 30-35% efficient in generating electricity (some newer natural gas plants are closer to 50-60%). This fact greatly reduces the overall efficiency of an electric car. When we consider the total efficiency, from getting the energy from its natural source to the car moving down the highway, we find that the electric car is only about 20% efficient, while the internal combustion engine automobile is about half that at 10%4.

Turbine Generator

These same types of rules apply to a hydroelectric dam. Not all of the potential energy of the water behind the dam is realized. The water running through the pipes encounters drag forces from the pipe walls. The water hitting the turbines generates some heat, as does any type of collision. The water leaving the turbine still has some kinetic energy, which is energy not given to the turbine. Accounting for all of the energy losses in the system, the system is still about 80-90% efficient, which is one of the highest efficiencies for any type of electricity generating facility that we use in society today.

In this week's experiment, we are going to model this system in the laboratory. This type of generator can be purchased from scientific equipment supplies, along with probes that will measure the amount of electricity generated (the unit in Figure  was purchased from Pasco Scientific). This experiment transfers the potential energy of water from a plastic container that is placed a height H above the generator to the kinetic energy of the moving turbine blades on the generator. The generator then transfers this kinetic energy to electrical energy by spinning a magnetic in the wire coil on the top of the generator. This electrical energy will be sent to a computer that will monitor the output. From the energy measured by the computer, we will plot the dependence of potential energy on height, as well as calculating the efficiency of energy transfer in the turbine generator.

As stated previously, the amount of gravitational potential energy that an object has should depend upon the height through which it is allowed to fall. Theoretically, this dependence should be linear, i.e. the amount of gravitational potential energy an object is equal to some constant times the height of the object. Therefore, if everything else in the system is linear, this means that the amount of electrical energy produced should depend linearly on the height of the water.

Figure : Turbine Generator

The other issue that we are going to investigate is the efficiency of the total energy transfer from gravitational potential energy to electrical energy. By plugging in the height of each individual run, this formula gives us the total amount of energy in the system at the start. The computer will measure the amount of electrical energy that is output by the generator. Thus, we should be able to compute the efficiency of the system using the formula:

Efficiency = (electrical energy output)/(potential energy)

= (electrical energy output)/[(9800 J/m4) x VH]

When using this formula in the lab, be sure that both the electrical energy output and the potential energy have the same units of energy. If you measure V in cubic meters and H in meters, then the units for potential energy should be in joules, which is a watt-second. Ask your instructor to make sure that you are using the proper units on your lab.

Pumped hydroelectric energy storage (PHES)

Pumped hydroelectric energy storage (PHES) is a mature technology that has been deployed for over a century.3 Examples of installed PHES systems as early as 1890 can be found in both Italy and Switzerland. PHES does not generate electricity, rather is a storage mechanism.4 PHES uses electricity to pump water uphill to be stored, then energy is later recaptured when the water released back down hill through a turbine PHES systems are highly efficient, capable of reaching and surpassing 80-85% round-trip efficiencies. Thescale of PHES this paper addresses is suited to the functional ability of the Francis turbine.The Francis turbine is capable of reversible operation, utilizing a single unit that acts as a motor-pump or a turbine-generator. Figure 2-3 shows a basic schematic of the PHES installation at Raccoon Mountain owned and operated by the Tennessee Valley Authority (TVA

 

Figure : A basic schematic of the pumped hydro installation at Raccoon Mountain