Site pages
Current course
Participants
General
MODULE 1.
MODULE 2.
MODULE 3.
MODULE 4.
MODULE 5.
MODULE 6.
MODULE 7.
MODULE 8.
MODULE 9.
Topic 10
Lesson 6. Corrections In Chain Surveying
Chain survey is the simplest method of surveying. It is the exercise of physically measuring horizontal distances. In this method the lengths of lines marked on the field are measured, while the details are measured by offsets and ties from these lines. This field work will continue for 3 field hours. This is most suitable adapted to small plane areas with very few details.
Tape Corrections: - Precise measurements of distance is made by means of a steel tape 30 m or 50 m in length. Before use it is desirable to ascertain its actual length (absolute length) by comparing it with the standard of known length, which can be done for a small fee by the Survey and Standards department. It is well to note here the distinction between the nominal or designated length and absolute length of a tape. By the former is meant it’s designated length, e.g. 30 m, or 100 m, while by the latter is meant it’s actual length under specified conditions. The tape may be standardized when supported horizontally throughout its full length or in catenary. The expression that “a tape is standard at a certain temperature and under a certain pull” means that under these conditions the actual length of the tape is exactly equal to its nominal length. Since the tape is not used in the field under standard conditions it is necessary to apply the following corrections to the measured length of a line in order to obtain its true length:
Correction for absolute length, (ii) Correction for temperature, (iii) Correction for tension or pull, (iv) Correction for sag, and (v) Correction for slope or vertical alignment.
A correction is said to be plus or positive when the uncorrected length is to be increased, and minus or negative when it is to be decreased in order to obtain true length.
Correction for Absolute Length: - It is the usual practice to express the absolute length of a tape as its nominal or designated length plus or minus a correction. The correction for the measured length is given by the formula,
Ca = Lc / l ------------------- (1)
Where Ca = the correction for absolute length.
L = the measured length of a line.
l = the nominal length of a tape.
C = the correction to a tape.
The sign of the correction (Ca) will be the same as that of c. it may be noted that L and l must be expressed in the same units and the unit of Ca is the same as that of c.
Correction for Temperature: - It is necessary to apply this correction, since the length of a tape is increased as its temperature is raised, and consequently, the measured distance is too small. It is given by the formula,
Ct = a (Tm – To)L-----------(2)
in which Ct = the correction for temperature, in m.
a = the coefficient of thermal expansion.
Tm = the mean temperature during measurement.
To = the temperature at which the tape is standardized.
L = the measure length in m.
The sign of the correction is plus or minus according as Tm is greater or less
than To. The coefficient of expansion for steel varies from 10.6 x 10-6 to 12.2 x 10-6 per degree centigrade and that for invar from 5.4 x 10-7 to 7.2 x 10-7. If the coefficient of expansion of a tape is not known, an average value of 11.4 x 10-6 for steel and
6.3 x 10-7 for invar may be assumed. For very precise work, the coefficient of expansion for the tape in question must be carefully determined.
Correction for Pull (or Tension): - The correction is necessary when the pull used during measurement is different from that at which the tape is standardized. It is given by the formula,
Cp = (P-Po)L / AE ----------(3)
Where Cp = the correction for pull in metres.
P = the pull applied during measurement, in newtons (N).
Po= the pull under which the tape is standardized in newtons (N).
L = the measured length in metres.
A = the cross-sectional area of the tape, in sq.cm.
E = the modulus of elasticity of steel.
The value of E for steel may be taken as 19.3 to 20.7 x 1010 N/m2 and that for invar 13.8 to 15.2 x 1010 N/m2. For every precise work its value must be ascertained. The sign of the correction is plus, as the effect of the pull is to increase the length of the tape and consequently, to decrease the measured length of the line.
Correction for Sag: - (Fig.1). When a tape is stretched over points of support, it takes the form of a catenary. In actual practice, however, the catenary curve is assumed to be a parabola.
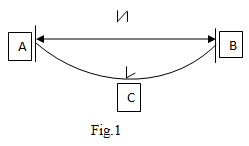
The correction for sag (or sag correction) is the difference in length between the arc and the subtending chord (i.e., the difference between the horizontal distance between supports and the length measured along the curve). It is required only when the tape is suspended during measurement. Since the effect of the set on the tapes is to make the measured length too great this correction is always subtractive. It is given by the formula,
Cs = l1 (mgl1)2 / 24P2 = l1(Mg)2 / 24P2 ………………(4)
in which Cs = the sag correction for a single span, in metres.
l1 = the distance between supports in metres.
m = the mass of the tape, in kilograms per metre.
M = Total mass of the tape in kilograms.
P = the applied pull, in newtons (N).
If there are n equal spans per tape length, the sag corrections per tape length is given, by
Cs = nl1(mgl1)2 / 24P2 = l(mgl1)2 / 24P2 = l(mgl)2 / 24n2P2 ………….(4a)
in which l = the length of the tape = nl1, and l1= l/n.
Normal Tension: - The normal tension is a tension at which the effects of pull and sag are neutralized, i.e. the elongation due to increase in tension is balanced by the shortening due to sag. It may be obtained by equating the corrections for pull and sag. Thus we have,
(Pn-Po)l1 / AE = l1(mgl1)2 / 24Pn2 or (Pn-Po) Pn2 = W2AE / 24
~ Pn = 0.204 W √AE / √(Pn-Po) …………………………………………..(5)
in which Pn = the normal tension in newtons (N).
W = the weight of the length of tape between supports in newtons (N).
The value of Pn may be determined by trial.
Correction for Slope or Vertical Alignment: - (Fig 2) This correction is required when the points of support are not exactly at the same level.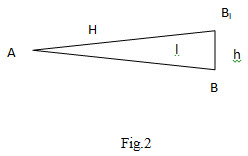
Let l1 l2, etc. = the lengths of successive uniform slopes.
lt1, lt2 etc. = the differences in height between the extremities of each of these
slopes.
Cs = the total correction for slope.
If l is the length of any one slope, and h the difference in height between the ends of the slope,
the slope correction = l - √ l2-h2
= l – l (1 – h2 / 2l2 – h4 / 3l4 – etc..)
=(h2 / 2l + h4 / 3l3 + etc.) = h2 / 2l ------------------------(6)
hence, Cs = (h12 / 2l1 + h22 / 2l2 + ….. + hn2 / 2ln) -------------------------------(6a)
When the slopes are of uniform length l we have
Cs = l / 2l (h12 + h22 + ……… + hn2) = ∑h2 / 2l -------------------------(6b)
This correction is always subtractive from the measured length. If the slopes are given in terms of vertical angles (plus or minus angles), the following formula may be used:
The correction for the slope = l – l cos 0 = 2l sin2 0 / 2
= l versin 0 (-ve) --------------------------(7)
in which l = the length of the slope : 0 = the angle of the slope.
Examples on Tape Corrections
Examples 1: - A line was measured with a steel tape which was exactly 30m long at 18oC and found to be 452.343 m. The temperature during measurement was 32oC. Find the true length of the line. Take coefficient of expansion of the tape per oC=0.0000117.
Temperature correction per tape length = Ct
= α (Tm - To) l
Here l = 30 m: To =18oC; Tm = 32oC;
α = 0.0000117
~ Ct = 0.0000117 (32-18) 30
= 0.004914 m (+ ve)
Hence the length of the tape at 32oC = 30 + Ct
= 30 + 0.004914 = 30.004914 m.
Now true length of a line = L’ / L x its measured length.
L = 30 m: L’ = 30.004914 m; measured length = 452.343 m.
~ True length = 30.004914 / 30 x 452.343 = 452.417 m.
Example 2: - A line was measured with a steel rape which was exactly 30 m at 18oC and a pull of 50 N and the measured length was 459.242 m. Temperature during measurement was 28oC and the pull applied was 100 N. The tape was uniformly supported during the measurement. Find the true length of the line if the cross-sectional area of the tape was 0.02 cm2, the coefficient of expansion
per oC = 0.0000117 and the modulus of elasticity = 21 x 106 N per cm2.
Temperature
Correction per tape length = α ( (Tm – To)L
= 0.0000117 x (28 -18) 30
= 0.00351 m (+ ve)
Sag correction per tape length = 0
Pull correction per tape length = (Pm - Po)L / AE
= (100 – 50)30 / 0.02 x 21 x 106
= 0.00357 m (+ve)
~ Combined correction = 0.00351 + 0.00357 m.
= 0.00708 m
True length of tape = 30.00708 m
True length of the line = 30.00708 / 30 x 459.242
= 459.350 m.
Example 3: - A 50 m tape is suspended between the ends under a pull of 150 N. The mass of the tape is 1.52 kilograms. Find the corrected length of the tape.
Correction for sag = Cs = l1 (Mg)2 / 24 P2
l1 = 50 m; M = 1.52 kilograms; P = 150 N.
~ Cs = 50 x (1.52 x 9.81)2 / 24 x 1502 = 0.0206 m.
~ Corrected length of the tape = l – Cs
= 50 – 0.0206
= 49.9794 m.
Example 4: - The downhill end of the 30 m tape is held 80 cm too low. What is the horizontal length?
Correction for slope = h2 / 2l
Here h = 0.8 m; l = 30 m
~ The required correction = 0.82 / 2 x 30 = 0.0167 m.
Hence the horizontal length = 30 – 0.0167
= 29.9833 m
Example 5: - A 100 m tape is held 1.5 m out of line. What is the true length?
Correction for incorrect alignment = d2 / 2l ( - ve)
Here d = 1.5 m; l = 100 m.
~ Correction = 1.52 / 2 x 100 = 0.011 m.
~ True length = 100 – 0.011 = 99.989 m.