Watershed Hydrology 3(2+1)

Lesson 16 Physical Characteristics of Watersheds

Watershed area is comprised of two subcomponents: 1) Stream areas 2) Inter-basin areas. 

The inter-basin areas are the surface elements contributing flow directly to streams of order higher than 1. 

Stream areas are those areas that would constitute the area draining to a predetermined point in the stream or outlet. 

For example, the stream area for first-order streams would be delineated by measuring the drainage area for each first-order channel. This classification of areas is useful in geomorphologic modeling of watershed runoff.

 

Horton (1945) inferred that mean drainage areas of progressively higher orders might form a geometric sequence. This characteristic was formulated as a law of drainage areas by Schumm (1954), who stated that the mean drainage areas of streams of each order tend to approximate a geometric progression as

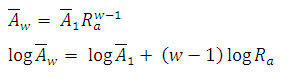
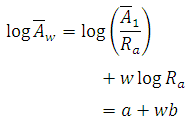
where  = mean area of basins of order w;  = mean area of first-order basins; and  R_a= Stream Area ratio defined as A_w/A_w-1and normally varies from 3 to 6.Drainage area is highly correlated with several hydrologic parameters, e.g., watershed discharge Q (Leopold and Miller, 1956; Hack, 1957). One of the simplest form is

Q

=KA^x

Wherek and x = parameters

Equations (1) and (2) can be combined to obtain an average flow for a watershed of given order as

Q_w

WhereQ_w = average flow for A_w; and Q₁ = average flow for A1 

16.2 Watershed Shape

Numerous symmetrical and irregular forms of drainage areas are encountered in practice. A frequently occurring shape is a pear shape in plan view, as shown in Fig.16.1a

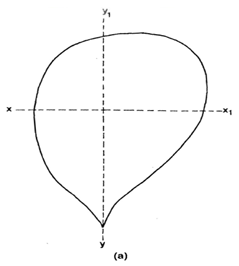
Fig. 16.1a.Typical pear shaped watershed.(Source: Singh, 1994)

The watershed surface, however, is always a tilted concavity that determines the general direction of flow. Depending upon the interaction of climate and geologic processes, the lateral section of a watershed may approximate a U shaped valley, Fig. 16.1b, or a V-shaped one, Fig. 16.1c.

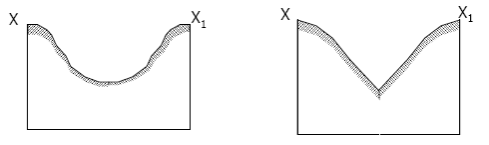
Fig. 16.1b.U-shaped valley.Fig. 16.1c.U-shapedvalley.

(Source: Singh, 1994)

The Transverse Section, Fig. 16.2d, displays increase in steepness towards the upstream area.

 

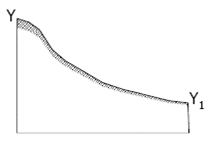
Fig. 16.1d.Cross-section along Y-Y₁.(Source: Singh, 1994)

A multitude of dimensionless parameters have been proposed to quantitatively define watershed shape. Some of the commonly used parameters are given in Table 16.1.

Table 16.1. Watershed shape parameters (Source: Singh, 1994)

                                  

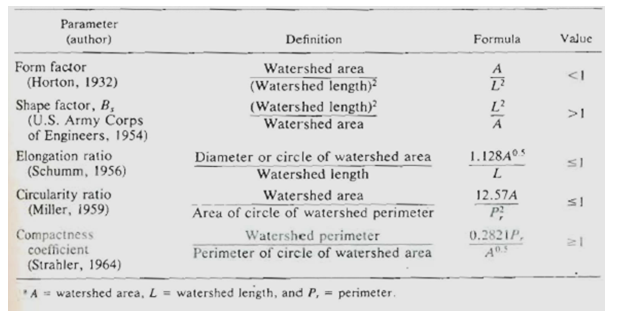
These factors involve watershed length L, area, and/or perimeter P_r.

Length is defined in more than one way: (1) The greatest straight-line distance between any two points on the perimeter, (2) The greatest distance between the outlet and any point on the perimeter, (3) The length of the main stream from its source (projected to the perimeter) to the outlet.

 

Fig. 16.2.Watershed Length Measurement.(Source: Singh, 1994)

Watershed shape influences the hydrograph shape, especially for small watersheds. If a watershed is long and narrow, then it will take longer for water to travel from watershed extremities to the outlet and the resulting runoff hydrograph will be flatter (Fig. 16.3a).

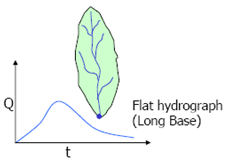
Fig. 16.3a.(Source: Singh, 1994)

For more compact watersheds, the runoff hydrograph is expected to be sharper with a greater peak and shorter duration (Fig. 16.3b).

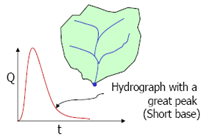
Fig. 16.3b.(Source: Singh, 1994)

For a watershed that is partly long and narrow, and partly compact, the runoff hydrograph is expected to be a complex composite of the aforementioned hydrographs (Fig. 16.3c).

Fig. 16.3c.(Source: Singh, 1994)

16.3 Watershed slope

Basin slope has a profound effect on the velocity of overland flow, watershederosion potential, and local windsystems.

Basin slope S is defined as,

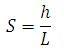 (16.4)

Whereh = fall in meters, and L = horizontal distance (length) over which the fall occurs.

 

16.4 Watershed Centroid

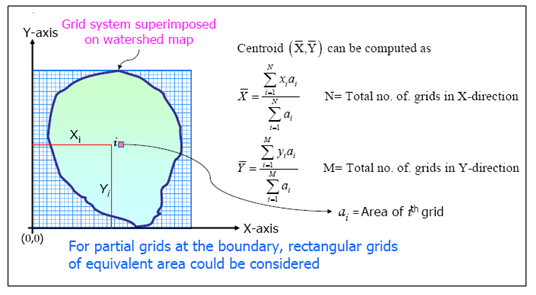
The centroid of a drainage basin is simply the location of the point within the drainage basin that represents the weighted centre of the basin. It is the first moment of the area about the origin. One method of locating the centroid, in the absence of necessary mathematical equations, is to use a cutout tracing of the drainage basin. Trial-and-error balancing of this tracing on the point of a pencil will locate the centroid sufficiently well for hydrologic uses. Another method that is used is to cut the basin map into equal grid sizes and equalize the weights of the cutout grids on a sensitive chemical balance. The centroid of a drainage basin can be determined more accurately by using the method of moments and representing the basin by a grid system.

 

 

16.5 Watershed Length

Basin length, Lb, is the longest dimension of a basin parallel to its principal drainage channel. Basin width can be measured in a direction approximately perpendicular to the length measurement. The relation between mainstream length and drainage-basin area for small watershed is given as (Gray, 1961).

WhereL_b is in km and A in km² 

 

References

Singh, V. P. (1994). Elementary Hydrology.Prentice Hall of India Private Limited, 80-114.

 

Suggested Reading

Suresh R. (2007). Soil and Water Conservation Engineering.Fourth edition, Standard Publishers Distributors, New Delhi.