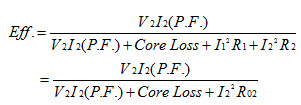Electrical M/C’s and Power Utilization 3(2+1)

LESSON 10. Power and energy efficiency, open circuit and short circuit tests, principles

 

5.1 Connections for open-circuit test

This power goes to supply the primary I²R loss and the core loss of the transformer. As the exciting current is very small, the primary I²R loss due to it may be neglected. Therefore, the wattmeter reads the transformer core loss. If the primary volt­age be varied and the core loss be determined for different values of voltage, a curve is obtained showing the relation of core loss to voltage. At no load the flux is practically proportional to the terminal voltage, as the primary impedance drop due to the no-load current is negligible. The eddy-current loss varies as the square of the voltage and the hysteresis loss as the 1.6 power of the voltage. The core loss will increase, therefore, nearly as the square of the voltage, as shown below (a).

Transformers are usually so designed that the most economical use of materials is obtained. Therefore, the core is operated at as high a flux density as the allowable core loss will permit. Figure 5.2 (a) shows that a slight increase of voltage, above rated voltage, produces a very large percentage increase in core loss. As transformers are rated by their maximum safe operating temperatures, this increased core loss may cause over­heating of the transformer. Therefore, the effect of operating transformers at over-voltage is to produce a large increase in temperature.

If the magnetizing current be plotted as abscissa, and the voltage as ordinates, a saturation curve similar to that of figure 5.2 (b) is obtained. The point marked "rated voltage" is the point on the saturation curve at which transformers are generally operated, and is well beyond the knee of the curve. Outside the question of increased core loss, the usual transformer cannot be operated at a voltage very much in excess of its rated voltage, for the exciting current increases very rapidly with small increase in voltage, as indicated in figure 5.2 (b). The flux density in the core is determined primarily by the per­missible core loss. Open-hearth annealed sheet steel, such as is used in dynamos, can be used for transformer cores. For a given flux density and frequency, however, silicon steel has much less core loss pen* unit volume than open-hearth steel, the effect of the silicon being to increase the electrical resistance, and hence reduce the eddy-current loss. Because of its small core loss, silicon steel may be operated safely at very high flux densities. The greater cost of silicon steel is more than offset by the saving in iron and in copper, and in the general reduction of the transformer dimensions.

Fig. 5.2. Characteristics; (a) Relation of core loss to voltage in a transformer (b) Relation of magnetising current to voltage in a transformer.

To obtain the true value of the exciting current; the current measured by the ammeter, should be resolved into two components, one of which lies along the voltage –E₁ or V and is shown as I_c in the figure 5.3 (-E₁ and V are practically equal at no load). This current I_c = I_O cos q is the energy component of the current and supplies the core losses. The quadrature component I_m = I_O sin q is the true magnetizing current.

Fig. 5.3 Phasor diagram

Short circuit test

Figure 5.4 shows the transformer short-circuited on the secondary side.

Fig. 5.4 Short circuit test

In a transformer, the impedance drop seldom exceeds 5 per cent of the rated voltage. If the 2,200 volt side of a transformer in figure 5.4  be used as the primary, the voltage necessary to send rated current through the windings on short-circuit is about 5 per cent  of 2,200, or 110 volts, which is a standard voltage for instrument coils. If the secondary of the transformer were rated at 220 volts, the voltage at short-circuit would be only 11 volts and the current would also be high. At this low voltage, high precision could not be obtained with ordinary instruments. When a primary current I₁ flows, the secondary current I₂ is equal to  I₁ (N₁/ N₂).  Therefore, no need of using an ammeter for measuring  I₂. The power delivered to the trans­former, goes to supply three losses; the primary copper loss, I₁²R₁, the secondary copper loss, I₂²R₂, and the core loss at short-circuit. The core loss is negligible, as 5 per cent, primary voltage means only about 2.5 per cent of the rated value of flux, since half the impressed voltage on short-circuit is consumed in the primary impedance drop. The core loss at 2 or 3 per cent, of the rated flux is so small as to be negligible, for the core loss varies nearly as the square of the flux. Therefore, the power at short circuit

where R₀₁ and R₀₂ are the transformer equivalent resistances referred to the primary and secondary, respectively. The value of equivalent resistance as found in this manner may be checked with the value determined by measuring the resistance of each winding with direct current. The ratio of effective to ohmic resistance is only a few per cent, greater than unity in most transformers. Figure 5.3 shows the equivalent circuit vector diagram for the short-cir­cuit test. This diagram is merely same as that of open circuit test, except that V2 now equals zero and all quantities are now referred to the primary side. It will be recognized that the entire voltage V1 is consumed in the impedance drops of the two windings. From this it is obvious that if Z₀₁ be the equiva­lent impedance of the transformer, referred to the primary side,

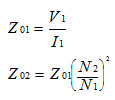
Knowing the equivalent impedance and equivalent resistance, the equivalent reactance is readily found as   for either primary or secondary side. In making the short-circuit and the open-circuit tests, the question of instrument losses should be investigated and correc­tion made if this be found necessary. As the losses in a trans­former are very small, the power taken by the instruments may be a considerable percentage of the power being measured.

Regulation and Efficiency

The data obtained from the short-circuit and open-circuit tests are sufficient to compute the regulation and the efficiency of the transformer at any load. As the equivalent resistance and reactance referred to either side are known, it is merely necessary to determine the regulation. The pro­cedure will be demonstrated by an example which follows. It has been pointed out that with constant voltage, the mutual flux of the transformer is practically constant from no load to full load. It usually does not vary more than from 1 to 3 per cent. Therefore, the core loss is practically constant at all loads and may be determined by the open-circuit test. For most purposes, it is necessary merely to measure the loss at the rated voltage of the transformer. The only other losses are the primary and secondary copper losses. These can be calculated readily, knowing the resistances of primary and secondary, or they may be computed from the equivalent resistance determined at short-circuit. The efficiency of the transformer may then be computed, since the losses are known. That is, the efficiency