System Engineering 3(3+0)

LESSON 4. Richard’s Growth Model

If n is positive, we will choose 1 + e^(t) and if n is negative we will choose 1 – e^(t).  For crop growth, we choose the sign of ‘n’ as positive and polynomial  (t) =  β - kt.  Therefore, Richard’s growth model is of the form

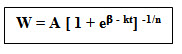
where   A = maximum growth

β, k and n = model parameters

If n =1, Richard’s growth model reduces to logistic growth model.  Normally for annual crops, the value of ‘n’ will be in and around one.  The mean relative growth rate is given by the formula  R = k / (n+1)

The Richard’s growth curve:

Richard’s growth model follows sigmoidal curve.  If the value of n is 1, then the curve will be almost at 45 degrees to X axis.

If the value of n is more than 1, the curve tends to fall down wards and if the value of n is less than 1, the curve becomes more upright.

Estimation of the model:

W = A [1 + e^{β - kt}]^-1/n

W/A = [1 + e^{β - kt}]^-1/n

Raising to the power ‘-n’ on both sides,

(W/A)^-n = 1 + e^{β - kt}

(A/W)ⁿ = 1 + e^{β - kt}

(A/W)ⁿ – 1 = e^{β - kt}

Taking log on both sides,

     log{(A/W)ⁿ –1} = log e^{β – kt}

                                = β – kt  = β + (- k) t

This is of the form Y = A + B x

                        Where  Y = log {(A/W)ⁿ –1}              x = t

A = β               or                     β = A

B = -k              or                     k = -B

We get the values of b and k by estimation.  To estimate the above form, we have to assume the value of n.  By estimating the value of R² and χ², we have to choose the most accurate value of n.  We should choose ‘n’ such that χ² value is minimum.

Ex.4. The following data gives the growth of LRA cotton grown during 1997 at TNAU in two nutrient treatments.  Estimate Richards growth models for both the treatments and test their validity.

Time	20	40	60	80	100	120	140	160
T1(g pl-1)	0.256	0.921	2.640	7.691	38.821	75.943	118.464	158.840
T2(g pl-1)	0.360	0.943	2.060	7.621	32.453	65.673	105.460	140.480

The maximum growth in T1 is 160 g pl-1 and in T2 145 g pl-1.  Choose the value of n for T1 as 1.26 and T2 as 1.14.

Solution:

The linear regression between  log {(A/W)ⁿ –1} and t is estimated and the estimated co-efficients are      

For T1             A = 10.144                  B = - 0.0847                (r = 0.987)

For T2             A = 8.6869                  B = - 0.0708                (r = 0.994)

The estimated model parameters are

For T1             β = 10.144                   k = 0.0847      

For T2             β = 8.6869                   k = 0.0708

The estimated growth models are

For T1             Ŵ= 160 [1 + e^{10.144 –0.0847 t}]^-0.7937

For T2             Ŵ= 145 [1 + e^{8.6869 – 0.0708 t}]^-0.8772

Validity of the models

Time (Days)	T1		T2
	W1	Ŵ1	W2	Ŵ2
20	0.256	0.196	0.360	0.246
40	0.921	0.750	0.943	0.851
60	2.640	2.865	2.060	2.923
80	7.691	10.752	7.621	9.810
100	38.821	36.971	32.453	30.170
120	75.943	93.030	65.673	72.312
140	118.464	140.290	105.460	115.680
160	158.840	155.917	140.480	136.501
χ2	7.628		2.607

 

Since the calculated χ² values are lower than the table χ² value, there is no significant differences between the predicted and observed values.  i.e. the models predict the crop growth satisfactorily and hence can be accepted.

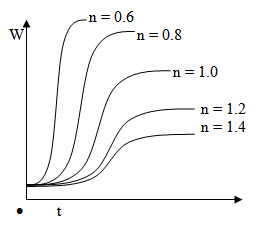
Gompertz’z Growth Model:

The model :

Gompertz’s growth model is of the form

W = A / exp[exp(a+bt)]

Where A = maximum growth

a and b = model parameters

The curve:

The curve is sigmoidal in shape

Estimation of growth rate:

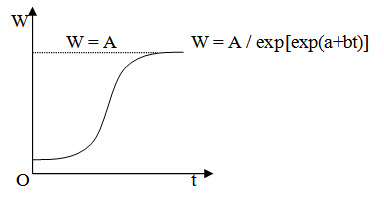
In Gompertz’s growth model, the relative growth (RGR) and growth rate (GR) can be estimated  as below

                          _{(a + bt)}

W = A / e^e

Taking log on both sides,

                                                _{(a + bt)}

Log W = log A –log e^e

                 = log A – e^a+bt

Differentiating with respect to t,

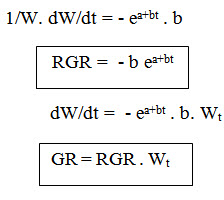
Estimation of the model:

Taking log on both sides,

log (A/W) = e^a+bt

Taking log again

      log [log (A/W)] = a + bt

This is of the form Y = a + bx

where Y = log [log (A/W)]     and     x = t

The co-efficients directly give the values of the parameters ‘a’ and ‘b’.

Ex.5. The following observation gives maize growth in two treatments.  T1 is herbicide spray and T2 is hand weeding.  Using Gompertz’s growth model, discuss which of the weed management practice is better, by estimating the RGR and GR on 20,40 and 60^th day.

Time	10	20	30	40	50	60	80	100	120
T1	1.74	2.69	6.40	25.81	82.34	112.39	134.26	162.10	199.88
T2	1.79	2.76	6.31	24.97	73.98	113.43	142.12	160.41	199.85

The maximum growth was found to be 200 g plant^-1 for both treatments.

Solution:

The linearity between log [log (A/W)] and t were estimated. The estimated model parameters are

For T1             a = 3.1440       b = - 0.066       (r = -0.0887)

For T2             a = 3.1073       b = -0.0654      (r = -0.893).

The estimated models are

For T1             Ŵ1 = 200 / exp[exp(3.144 – 0.066t)]

For T2             Ŵ2 = 200/ exp[exp(3.1073 – 0.0654t)]

Validity of the models

Time (Days)	T1		T2
	W1	Ŵ1	W2	Ŵ2
10	1.74	0.0012	1.79	0.0018
20	2.69	0.4073	2.76	0.4737
30	6.40	8.1303	6.31	8.6273
40	25.81	38.2058	24.97	39.0123
50	82.34	85.0091	73.98	85.4966
60	112.39	128.5246	113.43	128.5644
80	134.26	177.7167	142.12	177.4783
100	162.10	193.7874	160.41	193.6433
120	199.88	198.3212	199.85	198.2611
χ2	2554.63		1809.28

 

The estimated RGR and GR at 20^th, 40^th and 60^th days are

Time (Days)	T1		T2
	RGR	GR	RGR	GR
20	0.409	0.167	0.395	0.187
40	0.109	4.164	0.107	4.174
60	0.029	3.727	0.029	3.728

 

Inference

Since the calculated χ² values are greater than the table χ² value at 8 d.f., there exists significant difference between the predicted and observed values.  i.e. the model do not estimate the crop growth correctly.  Therefore, the models can not be used for this data.

The following can be inferred from the RGR and GR values,

• Herbicide spray (T1) registered high RGR than Hand weeding (T2) at 20. 40 and 60 days.  Therefore T1 is better than T2.

• Hand weeding (T2) registered higher GR at 20 and 40 days than herbicide spray (T2) probably due to better control of weeds.   However at 60 days, there is no difference in GR between treatments.

Gauss Growth Model:

The Model:

The Gauss growth model is of the form

W = A [1 – exp(a+bt²)]

Where A = maximum possible growth

a and b = model parameters

Estimation of growth rate:

The growth rate of Gauss curve is of the form,

GR = dW/dt = A . [- exp (a+bt²)] . 2bt

= - 2 Abt . exp(a+bt²)

Estimation of the model:

W = A [1 – exp(a+bt²)]

W/A = 1 – exp(a+bt²)

1-W/A =  exp(a+bt²)

Taking log on both sides,

Log (1-W/A) = a + bt²

i.e. Y = a + b X

where Y = log (1-W/A)           and      X = t²

Ex.6. The following observation gives the growth of maize in two seasons under the same treatment.  Test whether there is a change in growth rate between the seasons in maize growth or test whether the season has any influence on maize growth.

Time	10	20	30	40	50	60	80	100	120
W1	1.23	2.09	5.90	24.80	81.46	110.23	132.46	463.62	201.46
W2	1.41	2.01	5.89	22.32	74.39	101.46	124.83	148.56	182.32

The maximum dry weight recorded was 202 g plant^-1.

Solution:

The linearity between log (1-W/A) and t² was estimated.  The estimated model parameters are

For T1             a = 0.431                     b = - 0.00035               (r = -0.913)

For T2             a = 0.0368                   b = - 0.00016               (r = -0.989)

The estimated Gauss growth models are

Season 1          Ŵ1 = 202 [1 – exp(0.431 – 0.00035 t²)]

Season 2          Ŵ2 = 202 [1 – exp(0.0368 – 0.00016 t²)]

Validity of the models

Time (Days)	Season 1		Season 2
	W1	Ŵ1	W2	Ŵ2
10	1.23	-98.15	1.41	-4.25
20	2.09	-68.23	2.01	5.42
30	5.90	-24.45	5.89	20.53
40	24.80	24.45	22.32	39.76
50	81.46	72.42	74.39	61.52
60	110.23	113.83	101.46	84.19
80	132.46	168.91	124.83	126.73
100	163.32	192.61	148.56	159.69
120	201.46	199.99	182.32	181.07

 

The estimated growth rates are

Time	10	20	30	40	50	60	80	100	120
GRW1	2.10	3.78	4.76	4.97	4.53	3.70	1.85	0.66	0.17
GRW2	0.66	1.26	1.74	2.08	2.25	2.26	1.93	1.35	0.80

 

Inference

The growth rates are higher in season 1 at all stage of growth than in season 2.  Therefore, it can be concluded that season has an influence on growth rate of maize.  The estimated growth at 10, 20 and 30 days are negative.  Since, in biological systems, the growth can not be negative, the models do not estimate the growth properly.  Therefore, the models can not be accepted for predicting maize growth.