Site pages
Current course
Lesson -16 Queue
16.1 Introduction
Whether it is a railway reservation counter, a movie theater or print jobs submitted to network printer there is only one way to bring order to chaos from a queue. If you await your turn patiently there is more likelihood that you would get a better service.
Queue is a linear data structure that permits insertion of new element at one end and deletion of element at the other end. The end at which the deletion of an element take place is called front, and the end at which insertion of a new element can take place is called rear. The deletion or insertion of elements can take place only at the front or rear end of the list respectively.
The first element that gets added into the queue is the first one to get removed from the list. Hence, queue is also referred to as first-in- first-out (FIFO) list. The name queue comes from the everyday use of the term. Consider a queue of people waiting at a bus stop. Each new person who comes takes his or her place at the end of the line, and when the bus comes, the people at the front of the line board first. The first person in the line is the first person to leave. The figure 16.1 gives a pictorial representation of a queue.
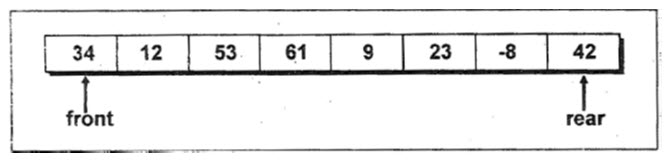 Figure 16.1 – Simple Queue
Figure 16.1 – Simple Queue
In Figure 16.1, 34 is the first element and 42 is the last element added to the queue. Similarly, 34 would be the first element to get removed and 42 would be the last element to get removed.
Applications of queue as a data structure are even more common than applications of stacks. While performing tasks on a computer, it is often necessary to wait one's turn before having access to some device or process. Within a computer system there may be queues of tasks waiting for the line printer, or for access to disk storage, or in a time sharing system for use of the CPU. Within a single program, there may be multiple requests to be kept in a queue, or one task may create other tasks, which must be done in turn by keeping them in a queue.
Let us now discuss how a queue can be represented in order to use it in a program.
16.2 Representation of a Queue as an Array
Queue, being a linear data structure can be represented in various ways such as arrays and linked lists. Representing a queue as an array would have the same problem that we discussed in case of stacks. An array is a data structure that can store a fixed number of elements. The size of an array should be fixed before using it. Queue, on the other hand keeps on changing as we remove elements from the front end or add new elements at the rear end. Declaring an array with a maximum size would solve this problem. The maximum size should be large enough for a queue to expand or shrink. Figure 16.2 shows the representation of a queue as an array.
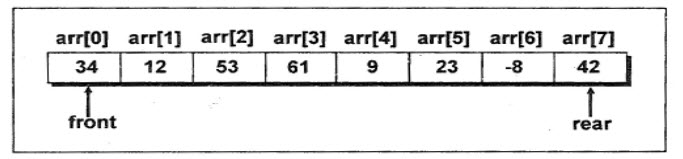
Figure 16.2 – Queue as an array
Let us now see a program that implements queue as an array.
#include <stdio.h>
#include <conio.h>
#define MAX 10
void addq ( int *, int, int *, int * ) ;
int delq ( int *, int *, int * ) ;
void main( )
{
int arr[MAX] ;
int front = -1, rear = -1, i ;
clrscr( ) ;
addq ( arr, 23, &front, &rear ) ;
addq ( arr, 9, &front, &rear ) ;
addq ( arr, 11, &front, &rear ) ;
addq ( arr, -10, &front, &rear ) ;
addq ( arr, 25, &front, &rear ) ;
addq ( arr, 16, &front, &rear ) ;
addq ( arr, 17, &front, &rear ) ;
addq ( arr, 22, &front, &rear ) ;
addq ( arr, 19, &front, &rear ) ;
addq ( arr, 30, &front, &rear ) ;
addq ( arr, 32, &front, &rear ) ;
i = delq ( arr, &front, &rear ) ;
printf ( "\nItem deleted: %d", i ) ;
i = delq ( arr, &front, &rear ) ;
printf ( "\nItem deleted: %d", i ) ;
i = delq ( arr, &front, &rear ) ;
printf ( "\nItem deleted: %d", i ) ;
getch( ) ;
}
/* adds an element to the queue */
void addq ( int *arr, int item, int *pfront, int *prear )
{
if ( *prear == MAX - 1 )
{
printf ( "\nQueue is full." ) ;
return ;
}
( *prear )++ ;
arr[*prear] = item ;
if ( *pfront == -1 )
*pfront = 0 ;
}
/* removes an element from the queue */
int delq ( int *arr, int *pfront, int *prear )
{
int data ;
if ( *pfront == -1 )
{
printf ( "\nQueue is Empty." ) ;
return NULL ;
}
data = arr[*pfront] ;
arr[*pfront] = 0 ;
if ( *pfront == *prear )
*pfront = *prear = -1 ;
else
( *pfront )++ ;
return data ;
}
Output:
Queue is full.
Item deleted: 23
Item deleted: 9
Item deleted: 11
Here we have used an array arr to maintain the queue. We have also declared two variables front and rear to monitor the two ends of the queue. The initial values of front and rear are set to -1, which indicate that the queue is empty. The functions addq( ) and delq( ) are used to perform add and delete operations on the queue.
While adding a new element to the queue, first it would be ascertained whether such an addition is possible or not. Since the array indexing begins with 0 the maximum number of elements that can be stored in the queue are MAX - 1. If these many elements are already present in the queue then it is reported to be full. If the element can be added to the queue then the value of the variable rear is incremented using the pointer prear and the new item is stored in the array. The addition of an element to the queue has been illustrated in Figure 16.3.
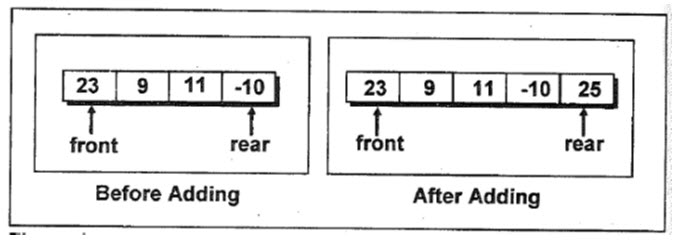
Figure 16.3 - Adding element to a queue
If the item being added to the queue is first element (i.e. if the variable front has a value -1) then as soon as the item is added to the queue front is set to 0 indicating that the queue is no longer empty.
Let us now see how the delq( ) function works. Before deleting an element from the queue it is first ascertained whether there are any elements available for deletion. If not, then the queue is reported as empty. Otherwise, an element is deleted form arr[*pfront]. The deletion of an element is illustrated in Figure 16.4.
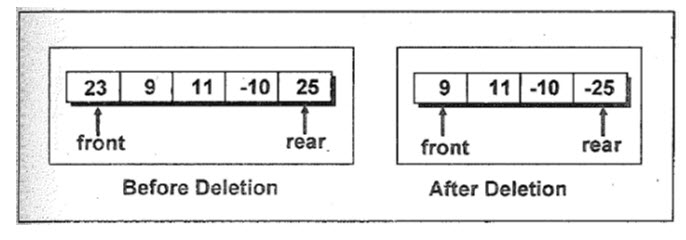
Figure 16.4 - Deleting elements from a queue
Imagine a case where we add 5 elements to the queue. Value of rear would now be 4. Suppose we have not deleted any elements from the queue, then at this stage the value of front would be 0. Now suppose we go on deleting elements from the queue. When the fifth element is deleted the queue would fall empty. To make sure that another attempt to delete should be met with an “empty queue” message, in. such a case front and rear both are reset to -1 to indicate emptiness of the queue.
But this program has got some limitations. Suppose we go on adding elements to the queue till the entire array gets filled. At this stage the value of rear would be MAX - 1. Now if we delete 5 elements from the queue, at the end of these deletions the value of front would be 5. If now we attempt to add a new element to the queue then it would be reported as full even though in reality the first five slots of the queue are empty. To overcome this situation we can implement a queue as a circular queue, which would discuss later in this chapter.
16.3 Representation of a Queue As a Linked-List
Queue can also be represented using a linked list. As discussed earlier, linked lists do not have any restrictions on the number of elements it can hold. Space for the elements in a linked list is allocated dynamically; hence it can grow as long as there is enough memory available for dynamic allocation. The item in the queue represented as a linked list would be a structure as shown below:
struct node
{
<dataType> data;
struct node *link ;
} ;
where dataType represents the type of data such as an int, float, char, etc. Figure 16.5 shows the representation of a queue as linked list.
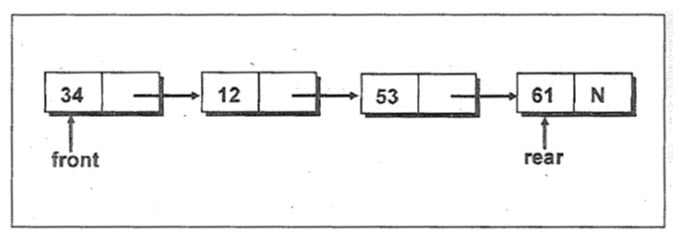
Figure 16.5 – Queue as a linked list
Let us now see a program that implements the queue as a linked list.
#include <stdio.h>
#include <conio.h>
struct node
{
int data ;
struct node *link ;
} ;
struct queue
{
struct node *front ;
struct node *rear ;
} ;
void initqueue ( struct queue * ) ;
void addq ( struct queue *, int ) ;
int delq ( struct queue * ) ;
void delqueue ( struct queue * ) ;
void main( )
{
struct queue a ;
int i ;
clrscr( ) ;
initqueue ( &a ) ;
addq ( &a, 11 ) ;
addq ( &a, -8 ) ;
addq ( &a, 23 ) ;
addq ( &a, 19 ) ;
addq ( &a, 15 ) ;
addq ( &a, 16 ) ;
addq ( &a, 28 ) ;
i = delq ( &a ) ;
printf ( "\nItem extracted: %d", i ) ;
i = delq ( &a ) ;
printf ( "\nItem extracted: %d", i ) ;
i = delq ( &a ) ;
printf ( "\nItem extracted: %d", i ) ;
delqueue ( &a ) ;
getch( ) ;
}
/* initialises data member */
void initqueue ( struct queue *q )
{
q -> front = q -> rear = NULL ;
}
/* adds an element to the queue */
void addq ( struct queue *q, int item )
{
struct node *temp ;
temp = ( struct node * ) malloc ( sizeof ( struct node ) ) ;
if ( temp == NULL )
printf ( "\nQueue is full." ) ;
temp -> data = item ;
temp -> link = NULL ;
if ( q -> front == NULL )
{
q -> rear = q -> front = temp ;
return ;
}
q -> rear -> link = temp ;
q -> rear = q -> rear -> link ;
}
/* removes an element from the queue */
int delq ( struct queue * q )
{
struct node *temp ;
int item ;
if ( q -> front == NULL )
{
printf ( "\nQueue is empty." ) ;
return NULL ;
}
item = q -> front -> data ;
temp = q -> front ;
q -> front = q -> front -> link ;
free ( temp ) ;
return item ;
}
/* deallocates memory */
void delqueue ( struct queue *q )
{
struct node *temp ;
if ( q -> front == NULL )
return ;
while ( q -> front != NULL )
{
temp = q -> front ;
q -> front = q -> front -> link ;
free ( temp ) ;
}
}
Output:
Item extracted: 11
Item extracted: -8
Item extracted: 23
In this program the structure queue contains two data member front and rear, both are of the type pointers to the structure node To begin with, the queue is empty hence both front and rear are set to NULL.
The addq () function adds a new element at the rear end of the list. If the element added is the first element, then both front and rear are made to point to the new node. However, if the element added is not the first element then only rear is made to point to the new node, whereas front continues to point to the first node in the list.
The delq() function removes an element from the list which is at the front end of the list. Removal of an element from the list actually deletes the node to which front is pointing. After deletion of a node, front is made to point to the next node that comes in the list, whereas rear continues to point to the last node in the list.
The function delqueue()is called before the function main() comes to an end. This is done because the memory allocated for the existing nodes in the list must be de-allocated.
16.4 Circular Queue
The queue that we implemented using an array suffers from one limitation. In that implementation there is a possibility that the queue is reported as full (since rear has reached the end of the array), even though in actuality there might be empty slots at the beginning of the queue. To overcome this limitation we can implement the queue as a circular queue. Here as we go on adding elements to the queue and reach the end of the array, the next element is stored in the first slot of the array (provided it is free). More clearly, suppose an array arr of n elements is used to implement a circular queue. Now if we go on adding elements to the queue we may reach arr[n-1]. We cannot add any more elements to the queue since we have reached the end of the array. Instead of reporting the queue as full, if some elements in the queue have been deleted then there might be empty slots at the beginning of the queue. In such a case these slots would be filled by new elements being added to the queue. In short just because we have reached the end of the array the queue would not be reported as full. The queue would be reported as full only when all the slots in the array stand occupied. Figure 16.6 shows the pictorial representation of a circular queue.
Figure 16.6 – Circular Queue
Let us now see a program that performs the addition and deletion operation on a circular queue.
#include <stdio.h>
#include <conio.h>
#define MAX 10
void addq ( int *, int, int *, int * ) ;
int delq ( int *, int *, int * ) ;
void display ( int * ) ;
void main( )
{
int arr[MAX] ;
int i, front, rear ;
clrscr( ) ;
/* initialise data member */
front = rear = -1 ;
for ( i = 0 ; i < MAX ; i++ )
arr[i] = 0 ;
addq ( arr, 14, &front, &rear ) ;
addq ( arr, 22, &front, &rear ) ;
addq ( arr, 13, &front, &rear ) ;
addq ( arr, -6, &front, &rear ) ;
addq ( arr, 25, &front, &rear ) ;
printf ( "\nElements in the circular queue: " ) ;
display ( arr ) ;
i = delq ( arr, &front, &rear ) ;
printf ( "Item deleted: %d", i ) ;
i = delq ( arr, &front, &rear ) ;
printf ( "\nItem deleted: %d", i ) ;
printf ( "\nElements in the circular queue after deletion: " ) ;
display ( arr ) ;
addq ( arr, 21, &front, &rear ) ;
addq ( arr, 17, &front, &rear ) ;
addq ( arr, 18, &front, &rear ) ;
addq ( arr, 9, &front, &rear ) ;
addq ( arr, 20, &front, &rear ) ;
printf ( "Elements in the circular queue after addition: " ) ;
display ( arr ) ;
addq ( arr, 32, &front, &rear ) ;
printf ( "Elements in the circular queue after addition: " ) ;
display ( arr ) ;
getch( ) ;
}
/* adds an element to the queue */
void addq ( int *arr, int item, int *pfront, int *prear )
{
if ( ( *prear == MAX - 1 && *pfront == 0 ) || ( *prear + 1 == *pfront ) )
{
printf ( "\nQueue is full." ) ;
return ;
}
if ( *prear == MAX - 1 )
*prear = 0 ;
else
( *prear )++ ;
arr[*prear] = item ;
if ( *pfront == -1 )
*pfront = 0 ;
}
/* removes an element from the queue */
int delq ( int *arr, int *pfront, int *prear )
{
int data ;
if ( *pfront == -1 )
{
printf ( "\nQueue is empty." ) ;
return NULL ;
}
data = arr[*pfront] ;
arr[*pfront] = 0 ;
if ( *pfront == *prear )
{
*pfront = -1 ;
*prear = -1 ;
}
else
{
if ( *pfront == MAX - 1 )
*pfront = 0 ;
else
( *pfront )++ ;
}
return data ;
}
/* displays element in a queue */
void display ( int * arr )
{
int i ;
printf ( "\n" ) ;
for ( i = 0 ; i < MAX ; i++ )
printf ( "%d\t", arr[i] ) ;
printf ( "\n" ) ;
}
Output:
Elements in the circular queue:
14 22 13 -6 0 0 0 0 0 0
Item deleted: 14
Item deleted: 22
Elements in the circular queue after deletion:
0 0 13 -6 25 0 0 0 0 0
Elements in the circular queue after addition:
0 0 13 -6 25 21 17 18 9 20
Elements in the circular queue after addition:
32 0 13 -6 25 21 17 18 9 20
Here the array arr is used to store the elements of the circular queue. The functions addq() and delq() are used to add and remove the elements from the queue respectively. The function display() displays the existing elements of the queue. The initial values of front and rear are set to -1, which indicates that queue is empty.
In main() first we have called the addq() function 5 times to insert elements in the circular queue. In this function, following cases are considered before adding an element to the queue.
First we have checked whether or not the array is full. The message 'Queue is full' gets displayed if front and rear are in adjacent locations with rear following the front.
If the value of front is -1 then it indicates that the queue is empty and the element to be added would be the first element in the queue. The values of front and rear in such a case are set to 0 and the new element gets placed at the 0th position.
It may also happen that some of the positions at the front end of the array are vacant. This happens if we have deleted some elements from the queue, when the value of rear is MAX -1 and the value of front is greater than 0. In such a case the value of rear is set to 0 and the element to be added is added at this position.
The element is added at the rear position in case the value of front is either equal to or greater than 0 and the value of rear is less than MAX - I.
Thus, after adding 5 elements the value of front and rear become 0 and 4 respectively. The display() function displays the elements in the queue. Figure 16.7 shows the pictorial representation of a circular queue after adding 5 elements .
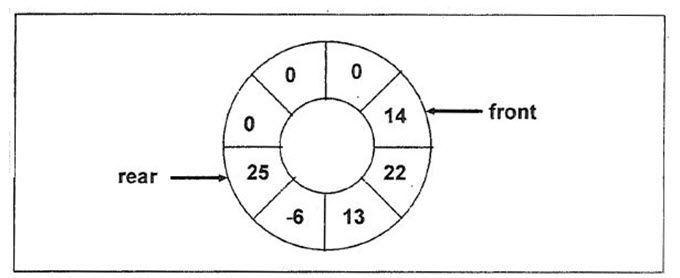
Figure 16.7 – Circular queue after adding elements
Next we have called delq() function twice to remove 2 elements from the queue. The following conditions are checked while deleting an element
First we have checked whether or not the queue is empty. The value of front in our case is 4, hence an element at the front position would get removed.
Next, we have checked if the value of front has become equal to rear. If it has, then the element we wish to remove is the only element of the queue. On removal of this element the queue would become empty and hence the values of front and rear are set to -1.
On deleting an element from the queue the value of front is set to 0 if it is equal to MAX - 1. Otherwise front is simply increment by 1. Figure 16.8 shows the pictorial representation of a circular queue after deleting two elements from the queue.
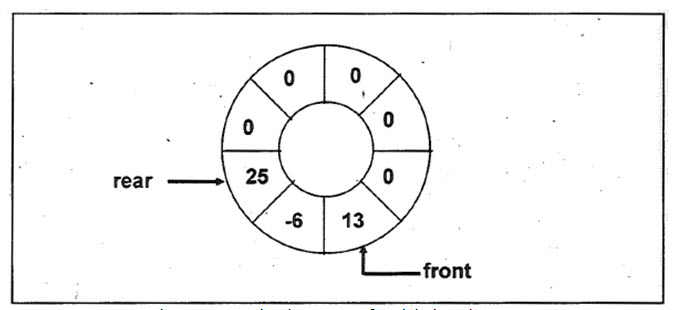
Figure 16.8– Circular queue after deleting elements
Further calls to addq() function adds elements 21,17, 18,9, and 20 to the queue. The value of front and rear at this stage becomes 2 and MAX - 1 respectively. One more call to addq() function changes the value of rear from MAX - 1 to 0 and the element added at the 0th position.