Site pages
Current course
Participants
General
Module 1. Moisture content and its determination.
Module 2. EMC
Module 3. Drying Theory and Mechanism of drying
Module 4. Air pressure within the grain bed, Shred...
Module 6. Study of different types of dryers- perf...
Module 5. Different methods of drying including pu...
Module 7. Study of drying and dehydration of agric...
Module 8. Types and causes of spoilage in storage.
Module 9. Storage of perishable products, function...
Module 10. Calculation of refrigeration load.
Module 11. Conditions for modified atmospheric sto...
Module 12. Storage of grains: destructive agents, ...
Module 13. Storage of cereal grains and their prod...
Module 14. Storage condition for various fruits an...
Module 15. Economics aspect of storage
Lesson.11 Mathematical Modeling of heat and Mass Transfer in Product
For proper equipment design, process optimization and improvement of final product quality, accurate prediction of the heat and moisture transfer in the product is vital. Many researchers have modeled the heat and moisture transfer in the food products during microwave heating and drying. They used numerical techniques based on the finite difference method, finite element method and transmission line matrix method to simulate the microwave heating with varying degree of accuracy.
Heat transfer and temperature profile within the product
In microwave heating, the governing energy balance equation includes a heat generation term Q by dielectric heating. Temperature changes at any location within a food during microwave drying are affected by thermal diffusion, generation of heat by microwaves and evaporation of moisture. Mathematically, it is represented as:
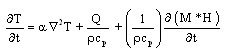 …(15)
…(15)
where, T is the product temperature, t is the time, Q is the conversion of microwave energy to heat per unit volume, M is the moisture concentration and H is enthalpy of moisture. The parameters a, r and cp are the thermal diffusivity, density and specific heat of the material, respectively.
The heat generated per unit volume of material (Q) is the conversion of electromagnetic energy in to heat energy. Its relationship with the average electric field intensity (Erms) at that location can be derived from Maxwell’s equations of electromagnetic waves as shown by Metaxax and Meredith (1983):
![]() …(16)
…(16)
where, f is the frequency of microwaves, Î0 is the dielectric constant of free space and β is the loss factor of food being heated. At a given frequency, the dielectric loss factor is a function of the composition of food materials and its temperature.
Mass transfer and moisture profiles
Assuming the food material as a capillary porous body, the governing equation for the internal moisture transport process can be written as:
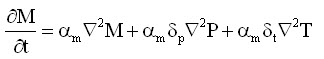 …(17)
…(17)
where, M is the total moisture content (liquid and vapour phase); am is the moisture diffusivity; dp and dt are the pressure and thermal gradient coefficients, respectively. The three terms in the right hand side of Eqn. 17 represent moisture movement due to concentration, pressure and temperature gradients, respectively. Flow due to thermal gradient is generally ignored during microwave drying of solid moist foods and the moisture movement is considered due to the pressure and concentration gradients.
Boundary and initial conditions
![]() …(18)
…(18)
The generalized boundary conditions for microwave heating can be written as:
where, ‘x’ represents the direction normal to the boundary and ‘kt’ is the thermal conductivity of the food material. The first term of the right hand side is for convective heat transfer at the surface with ‘h’, the convective heat transfer coefficient and ‘T¥’, the air temperature. Convective heat loss for a food under vacuum would be much lower due to low temperature gradient. The second term of the above equation involves radiative heat loss by the food material and Ts is the temperature of the surface facing the food material. The quantities Î and s are the surface emissivity and Stefan-Boltzman constant, respectively. Radiative heat transfer is important when the surfaces of the material act as susceptors. Evaporation (mw) at the surface is more important in microwave heating than in conventional heating because more moisture moves from the interior (Datta, 1990).
The boundary conditions for food samples in drying are featured by convective cooling and surface moisture loss. That is:
At x = ± l /2, -kt = 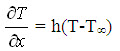 …(19)
…(19)
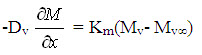 …(20)
…(20)
at x = 0, 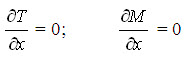
The initial sample temperature and moisture content are considered to be uniform
i.e. T = T0; Mv = Mv0; M = M0
where, l is the thickness of slices, Mv0 is the saturated vapour concentration at T0 and M0 is the initial moisture concentration of the food material.