Site pages
Current course
Participants
General
Module 1. Phase Rule
Module 2. Fuels
Module 3. Colloids Classification, properties
Module 4. Corrosion Causes, type and methods of p...
Module 5. Water Hardness
Module 6. Scale and sludge formation in boilers, b...
Module 7. Analytical methods like thermo gravimetr...
Module 8. Nuclear radiation, detectors and analyti...
Module 9. Enzymes and their use in manufacturing o...
Module 10. Principles of Food Chemistry
Module 11. Lubricants properties, mechanism, class...
Module 12. Polymers type of polymerization, proper...
Lesson 1. Phase rule and its application to one component system
1.1 INTRODUCTION OF PHASE RULE
The phase rule is a generalization given by Willard Gibbs (1874), which seeks to explain the equilibria existing in heterogeneous system. It may be stated as: “provided the equilibrium between any number of phases is not influenced by gravity, or electrical, or magnetic forces or by surface action and only by temperature, pressure and concentration, then the number of degrees of freedom (F) of the system is related to number of components (C) and of phases (P) by the phase rule equation for any system at equilibrium at a definite temperature and pressure.
F = C – P + 2
This rule, if properly applied, has no exception.
Explanation of terms:
1.2.1 Phase: A phase is defined as “an homogeneous, physically distinct and mechanically separable portion of system, which is separated from other such parts of the system by definite boundary surface”. For Example:
-
At freezing point, water consists of three phase :
Ice (s) ![]() Water (l)
Water (l) ![]() Water vapour (g)
Water vapour (g)
-
A gaseous mixture, being thoroughly miscible in all proportion, will constitute one phase only. Thus, a mixture of N2 and H2 forms phase only.
-
If two liquids are immiscible (i.e., benzene and water), they will form two separate phase only.
-
If two liquids are miscible (i.e., alcohol and water), they will form one liquid phase only.
-
A solution of a substance in a solvent consists of phase only, e. g, glucose solution in water.
-
Each solid mark up a separate phase, except in the case of solid solution, e. g, many forms of sulphur can exist together, but these are all separate phases.
-
A heterogeneous mixture like :
CaCO3 (s) ![]() CaO(s) + CO2 (g)
CaO(s) + CO2 (g)
Consists of three phases (i.e., two solids and one gasous). Similarly, in the equilibrium reaction,
Fe(s) + H2O ![]() FeO(s) + H2(g)
FeO(s) + H2(g)
There are two solid phases, Fe and FeO and one gaseous phase consisting of H2O(g) and H2(g). Thus, three phases exists in equilibrium.
- A homogeneous solid solution of a salt constitutes a single phase. Thus, Mohr’s [ FeSO4 (NH4)2SO46H2O] solution constitutes a single phase, although it consists of FeSO4 (NH4) SO4, and H2O.
1.2.2 Component: by the term component is meant “the smallest number of independent variable constituents, taking part in state of equilibrium, by mean of which the composition of each phase can be expressed in the form of chemical equation”. For example:
i. In the water system,
Ice (s) ![]() Water (l)
Water (l) ![]() vapour (g)
vapour (g)
The chemical composition of all the three phases is H2O. Hence, it is one component system.
ii. the sulphur system consists of four phases, rhombic, monoclinic, liquid and vapour, the chemical composition of all phases is S. hence, it is one component system.
iii. In the dissociation of NH4CI in a closed vessel,
NH4CI(g)![]() NH4CI(g)
NH4CI(g) ![]() NH3(g)+HCI(g)
NH3(g)+HCI(g)
The proportions of NH3 and HCl are equivalent and hence, the composition of both phases (solid and gaseous) can be expressed in terms of NH4CI alone. Hence, the number of component is one. However, if NH3 or HCl is in excess, the system become a two component system .
iv. A system of saturated solution of NaCI consists of solid salt, salt solution and water vapour. The chemical composition of all the three phases can be expressed in terms of NaCI and H2O. Hence, it is a two component system.
v. In the thermal decomposition of CaCO3
CaCO3(s) ![]() CaO(s) + CO2(g)
CaO(s) + CO2(g)
The composition of each of the three phases can be expressed in terms of at least any two of the independently variable constituents, CaCO3, Cao and CO2. Suppose CaCO3 and CaO are chosen as the two components, the composition of different phases is represented as follows:
Phase: CaCO3 = CaCO3 + 0 CaO
Phase: CaO = 0 CaCO3 + CaO
Phase: CO2 = CaCO3 – CaO
Thus, it is two component systems.
vi. In the dissociation reaction,
CuSO45H2O(s) ![]() CuSO4.3H2O(s) +2H2O(g)
CuSO4.3H2O(s) +2H2O(g)
The composition of each phase can be represented by the simplest component, CuSO4 and H2O
Hence, it is two component systems.
vii. In the equilibrium, Fe(s) + H2O(g)![]() FeO(s) + H2(g), the minimum components required the composition phase is three. Evidently, it is a three component system.
FeO(s) + H2(g), the minimum components required the composition phase is three. Evidently, it is a three component system.
Number of component of a system may alternatively be defined as the number of chemical constituents of the system minus the number of equations relating to these constituents in an equilibrium state. For example:
Dissociation of KClO3 in a closed vessel: following equilibrium exists :
KClO3(s)
2KCl(s) + 3O2 (g)
No. of constituents = 3
Now 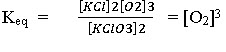
No. of equations relating the concentration of constituents =1.
Hence, number of components = 3-1 = 2 i.e., it is a two component system.
2. Dissociation of NH4Cl:
i. Only NH4Cl is heated in a closed vessel. The equilibrium existing is: NH4Cl(s) ![]() NH3(g) +HCl(g)
NH3(g) +HCl(g)
[NH3] = [HCl]
Also Keq =  = [NH3][HCl]
= [NH3][HCl]
Because the active mass of NH4Cl(s) is constant.
Now number of components, C
= No. of constituent –[ No, of equations relating to concentration of constituents]
= 3(NH4CL, NH3 and HCl) – 2 = I, i.e. it is a single component system :
ii. When NH4Cl is heated in a closed vessel along with NH3 or HCl, At equilibrium:
Keq = [NH3][HCl] ……………..(i)
But [NH3] ≠ [HCl] …………(ii)
Only one equation (i) relates the concentrations of constituents
No. of component, (C) = 3 -1 = 2, i.e. under the above conditions, the system has two components
1.2.3 Degree of freedom or variance: By the term “degree of freedom is meant by” the minimum number of independently variable factors, such as temperature, pressure and composition of the phases, which must be arbitrarily specified in order to represent perfectly the condition of a system. For example
i. In case of water system, Ice(s ) ![]() Water(l)
Water(l) ![]() Vapour(g), if all the three phases are present in equilibrium, then no condition need to be specified, as the three phases can be in equilibrium only at particular temperature and pressure. If condition (e.g. Temperature or pressure is altered, three phases will not remain in equilibrium and one of the phase disappears.
Vapour(g), if all the three phases are present in equilibrium, then no condition need to be specified, as the three phases can be in equilibrium only at particular temperature and pressure. If condition (e.g. Temperature or pressure is altered, three phases will not remain in equilibrium and one of the phase disappears.
ii. For a system consisting of water n in contact with its vapour,
Water(l) ![]() Vapour(g)
Vapour(g)
We must state either the temperature or pressure to define it completely. Hence, degree of freedom is one or system is univariant.
iii. For a system consisting of water vapour phase only, we must the values of both the temperature and pressure in order to describe the system completely. Hence, the system is bivariant or has two degrees of freedom.
iv. For a system consisting of ,
NaCl(s) ![]() NaCl (aq)
NaCl (aq) ![]() water vapour (g).
water vapour (g).
We must state either the temperature or pressure, because the saturation solubility is fixed at a particular temperature or pressure. Hence, the system is univariant
v. For a gaseous mixture of N2 and H2, we must state both the pressure and temperature, because if pressure and temperature are fixed, the volume automatically becomes definite. Hence, for a gaseous system, two factors must be stated in order to define it completely and thus, it has two degree of freedom (or bivariant system).
1.2.4 Merits of phases rule:
1. It is applicable to both physical and chemical equilibria.
2. It require no information regarding molecular/ micro-structure, since it is applicable to
macroscopic system.
3. It is a convenient method of classifying equilibrium states in terms of phases, components
and degrees of freedom.
4. It helps us to predict the behaviour of a system, under different sets of variables.
5. It indicates that different systems with same degree of freedom behave similarly.
6. It does not take into cognizance of either the nature or quantities of component present in
the system.
7. It helps in deciding whether under a given set of condition:
a. various substances would exist together in equilibrium or
b. some of the substances present would be interconverted or
c. some of the substances present would be eliminated .
1.2.5 Limitation of phase rule:
1. It can be applied only for system in equilibrium. Consequently, consequently, it is of little value in case of very slow equilibrium state attaining system.
2. It applies only to a single equilibrium system: and provided no information regarding any other possible equilibria in the system.
3. It requires utmost care in deciding the number of phases existing in an equilibrium sate, since it considers only the number of phases, rather than their amounts. Thus, even if a trace of the phase is present, it accounts towards the total number of phases.
4. It conditions that all phases of the system must be present simultaneously, under the identical conditions of temperature and pressure.
5. It conditions that solid and liquid phases must not be in finely –divided state; otherwise deviations occurs.
1.3 DERIVATION OF PHASE RULE
Consider a heterogeneous system having P phases and C components. Now according to definition the degree of freedom (F) of the system is minimum of independent variables which must be fixed arbitrarily to define the system completely. But the number of these variables is equal to the total number of variable minus the number of relations between them at equilibrium, since each relation diminishes the number of independent variables by one.
Now let us calculate the total number of independent variables:
i. Temperature: At equilibrium, temperature of every phase is same, so there is only one temperature variable for the entire system.
ii. Pressure: At equilibrium , each phase has the same pressure, so there is only one pressure variable for the entire system.
iii.Concentration : Concentration of each components is generally expressed in terms of mole fractions. As a rule, the number of composition variables required for each phase are (C-1), since the composition of all components may be expressed by stating the mole fraction of all except one of the components. For example, it there are two components A and B in one phase and if we know the concentration. (or mole fraction) of one (say A), the concentration of other (i.e,,B) can be automatically found, because the sum is always unity. Thus, if mole fraction of A is 0.4, that of B is known to be 1-0.4 or 0.6. Similarly, if we have three components and if the composition of two is known that of the third can be found out. Thus, if we have C components, we must know the concentration of C-1 component. So for P phases the total composition variable are p (C – 1).
Hence .Total number of variables
= 1(for temperature) + 1(for pressure) + P (C – 1) (for composition)
= P (C – 1) + 2
Now let us calculate the number of relations at equilibrium. We know that for a system in a thermodynamic equilibrium, the chemical potential (u), which is related to concentration of component in all the particular component I, we have at equilibrium :
[µi]α = [µi]β = [µi] γ
Consequently, there are two equilibrium relationships for each component if there are 3 phases. Hence, for P phases, the number of such relationships for each component are ( P -1),
Consequently, for C components, such relationships will be C ( P – 1),
iv. Degree of freedom , F = Total number of independent variables
No. of relationships between these variables
= [ P( C-1)+2] – [C(P-1)]
= C – P + 2.
This is nothing but mathematical statement of phase rule.
1.3.1 PHASE RULE FOR CHEMICAL REACTION EQUILIBRIUM
In a chemical reaction , various reactant with one another forming products. Consequently, the phase equilibrium become rather complicated due to simultaneous presence of reactants and products. Let Ne be the total number of chemical substances present in the overall system at equilibrium and r be the number of reactants, then the component term C of the phase rule equation is replaced by (Ne – r ), i.e,,,
C = Ne – r
Hence, phase rule equation becomes :
F = C –P + 2 =(Ne – r ) – p +2.
Illustration: let us consider the reaction oxygen with carbon producing a mixture of carbon monoxide and carbon dioxide. Thus :
C(s) + O2 (g) -----------à CO2
C (s) + ½ O2 (g)------------------à CO(g)
No. of phases at equilibrium (P)
= Solid phase due to carbon + Gaseous phase due to CO2+ CO + O2
= 1 + 1 = 2
No. of reactants ® = Carbon + oxygen
= 1 + 1 = 2
No. of chemical substances present at equilibrium (Ne)
= Carbon + CO2+ CO + O2
= 1 + 1+ 1+ 1 = 4
- Degree of freedom (F) = (Ne – r ) – p + 2 =(4 – 2) – 2 + 2 = 2
1.3.2 WATER SYSTEM
The water system consists of three phases , viz., ice, water and water vapour.
Ice(s) ![]() Water (I)
Water (I) ![]() Water vapour (g)
Water vapour (g)
Since H2O is the only chemical compound involved, therefore, it is single or one-component system . From the phase rule, when C =1,
F = C – P + 2 =1 – P + 2 = 3 – P
i.e, the degree of freedom depends on the number of phases present at equilibrium. Three different case are possible :
(i) P = 1 ; F = 2 (bivariant system)
(ii) P = 2 ; F = 1 (univariant system)
(iii) P = 3 ; F = 0 (invariant system)
From the above , it is clear that for any one-component system , the maximum number of degrees of freedom is two. Therefore, such a system can be represented completely by a two-dimensional
Diagram. The most convenient variable are the pressure and the temperature. The water system is shown in Fig. 1 The diagram consists of :
1. Areas : AOB. AOC and BOC are the fields of existence of vapour, liquid and ice phase respectively Within these single-phase areas, the system in bivariant , because to locate any point in an area, temperature as well as pressure co-ordinates need to be know.. This also following from phase rule equation : F = 3 – P = 3 – 1 = 2 .
2. Boundary lines: separating the areas are lines OA, OB and OC, connecting the point at which two phases can co-exist in equilibrium. In order to locate any point on a particular line, either temperature or pressure co-ordinate should be known, because for fixed value of one co-ordinate, the second is automatically fixed, In other words, any point on boundary lines has one degree of freedom or is univariant. This also follows from phase rule equation : F = 3 – P = 3 – 2 = 1.
The curve OA, dividing the liquid from the vapour region, is called vapour pressure curve of liquid water or vaporization curve. At any given temperature, there is one and only one pressure at which water vapour is in equilibrium with liquid water. Similarly , at any given pressure, there is one temperature at which water vapour is in equilibrium with liquid water. In other words, the system is univariant. i.e,, has one degree of freedom. The curve OA has a natural upper limit at +374 C. which is the critical-point, beyond which the phase merges into vapour phase and they are no longer distinguishable from each other.
The curve OB is the sublimation curve of ice. It gives the conditions under which water vapour is in equilibrium with solid ice. The point B has a natural limit at -273oC, beyond which the two phases merge into each other.
The curve OC , which divies the solid –ice region from the liquid – water region, is called melting curve, because it indicates how the melting temperature of ice or the freezing tempereature of water varies with the pressure. The slope of OC towards the pressure axis shows that the melting point of ice is decreased by increasing pressure.
3. Triple point: The three curves OA, OB, and OC meet at O, at which solid, liquid and vapour are simultaneously at equilibrium. This point at 273.16 k is called a triple – point. Since three phases co-exist, the system is invariant (F=3-3=0). In other words, there is no degree of freedom at O, i.e., neither pressure nor temperature can be altered, even slightly, without causing the disappearance of one of the phase.
4.Metastable curve OA’: As water does not always freeze at 0oC, so if the vessel containing water and vapour is perfectly clean and free from dust, it is possible to super – cool water several degrees below its freezing point 0. The dotted curve OA’, a continuation of vaporization curve AO, represents the pressure curve of super cooled water. This curve represents a metastable system. On slight disturbance, the super cooled water at once changes to solid ice. It may be noted that metastable vapour pressure of supper cooledh water is higher than the vapour pressure of ice.
5 Polymorphism:
Timman and Bridgman showed that water under high pressure (upto 5 X103 atm), exists in six other forms, besides ordinary ice (called ice I), which are stable under different conditions of temperature and pressure. These polymeric forms of ice (called ice I to ice VII) differ in crystalline structure, density and other physical properties. Consequently, each of these polymeric ice form constitutes a separate bphse. The equilibria between different polymeric forms of ice are represented in fig.-1.2 . It may be pointed that ice IV has not been shown in the diagram, since it has been isolated. From the diagram, it is evident that:
Regions I,II,III,V,VI and VII indicate stability of ice in these regions
Except ice II, all other forms of ice can coexist withj water.
Melting point of ordinary ice I is lowered by the increase of pressure and it falls to about -22oC at a pressure of 2040 atm. Further, pressure increase results in transformation of ice I to ice III, whose melting point is raised by the increase of pressure.
The ice II can be obtained from ice I,II or V.
It is possible to obtain not only the ordinary triple point O for ice – water – vapour equilibrium, but also other triple points (C,D,E,F and G). At these point, three phases can coexist, Viz. (a) three form of ice, or (b) two forms of ice and liquid water. All these triple points are invariant (F=0).
Not more than three phases cannot exist in equilibrium, because:
P =4 (let),C=1 F=C-P +2 = 1- 4+2 = -1
Negative value of F has no meaning.
7. At a high pressure, the melting point of ice is considerably raised and ice VII melt at 190 oC at a pressure of 40000 atm. This is an astonishing fact.