Engineering Properties of Biological Materials and Food Quality 3(2+1)

Lesson 3. Physical properties of biomaterials like shape, size, volume and surface area

 3.1. SIZE:

Size is an important physical attribute of foods used in screening solids to separate foreign materials, grading of fruits and vegetables, and evaluating the quality of food materials. In fluid flow, and heat and mass transfer calculations, it is necessary to know the size of the sample. Size of the particulate foods is also critical as it affects the viscosity and dispersibility and stability of the product. In the context of postharvest operations, agro-produce size determination is important for several reasons (Moreda et al., 2009)

• It allows the sorting of fresh market various agro produces into size groups. This is helps in assigning market and price differentials of large and small produce, to match consumer preferences and to allow pattern packing. Pattern packing provides better protection of the produce, utilizes the volume in the shipping container, owing to the higher packing density that can be achieved with commodities of homogeneous sizes in comparison to that of jumble packing.

• Size determination is mandatory for modern or on-line fruit/ vegetables/ grain/spices density sorting, for which two size-related parameters, volume and weight, are required.

• Size measurement is important for determining produce surface area. The latter is also of use for quantifying the microbial population on the surface of a foodstuff, for assessing the rates of heat, water vapor and gas transfer, or for estimating the throughput of peeling operations.

• Fruit size can provide useful information for suitable working of some internal quality (IQ) sensors.

• Grading of agro produce into size groups is often necessary in the food industry, to meet the requirements of some primary and secondary processing machines, or to assign process differentials of large and small produce.

• Shape features can be measured independently or by combining size measurements. Hence, the determination of agro commodity size parameters allows simple shape sorting.

 Produce can be sized according to different physical parameters, such as diameter, length, weight, volume, circumference, projected area, or any combination of these. It is easy to specify size for regular particles in terms of their major dimensions like length, width and thickness or major and minor diameter, but for irregular particles the term size must be arbitrarily specified.

3.1.1. Methods of measurement of size:

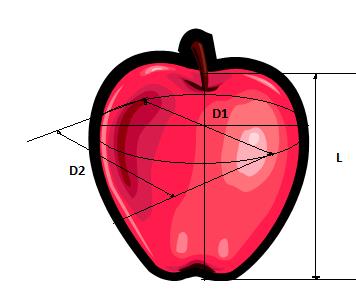
3.1.1.1. Projected area method

 Size can be determined using the projected area method (fig 3.1). In this method, three characteristic dimensions are defined:

 

1. Major diameter, which is the longest dimension of the maximum projected area

2. Intermediate diameter, which is the minimum diameter of the maximum projected area or the maximum diameter of the minimum projected area.

3. Minor diameter, which is the shortest dimension of the minimum projected area.

Length, width, and thickness terms are commonly used that correspond to major, intermediate, and minor diameters, respectively

 

Figure 3.1 Size determination by projected area method

3.1.1.2. Micrometer measurement:

The dimensions can be measured using a micrometer or caliper (fig. 2a), grain shape tester. The micrometer is a simple instrument used to measure distances between surfaces. Most micrometers have a frame, anvil, spindle, sleeve, thimble, and ratchet stop (fig 2b). They are used to measure the outside diameters, inside diameters, the distance between parallel surfaces, and the depth of holes.

 

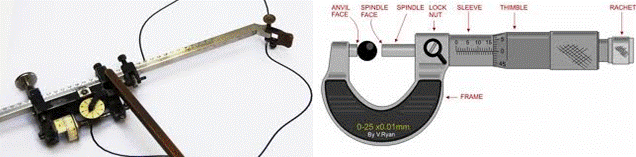
Fig. 3.2a. vernier caliper                                     fig. 3.2b. Micrometer

3.1.1.3. Grain shape tester:

It consists of a plunger and a horizontal surface, in between which the grains is held and dimensions are measured by dropping down the plunger on to the grain body.

3.1.1.4. Electronic system:

Various electronic systems are employed to sort agro commodities through off-line or on-line inspection. This saves labour cost and eliminates human error. Some of the commercial and non-commercial systems used for agro produce sorting are as follows (Moreda et al., 2009):

• Systems based on measurement of the volume of the gap between the fruit and the outer casing of embracing gauge equipment.

• Systems that calculate fruit size by measuring the distance between a radiation source and the fruit contour, where this distance is computed from the time of flight of the propagated waves.

• Systems that rely on the obstruction of light barriers or blockade of light

• Two-dimensional (2-D) machine vision systems such as digital images received by web cameras, CCD cameras.

• Three-dimensional (3-D) machine vision systems such as multi spectral and hyperspectral imaging system.

• Other systems. This group includes systems based on internal images, such as computed tomography (CT) or magnetic resonance imaging (MRI), X-ray, ultrasound techniques as well as some other approaches not included in the other groups.

3.2. SHAPE:

Shape describes the object in terms of a geometrical body. Shape is also important in heat and mass transfer calculations, screening solids to separate foreign materials, grading of fruits and vegetables, and evaluating the quality of food materials. The shape of a food material is usually expressed in terms of its sphericity, aspect ratio, ellipsoid ratio and slenderness ratio. Some of the shapes and their descriptions are given below in table 3.1. [Mohsenin, 1980]

Table 3.1: shape and description of various agro commodities

Shape	Description	Examples
Round	Approaching Spheroid	sapota, cherry tomato, pea
Oblate	Flattened at the stem end and apex	orange, pumpkin
Oblong	Vertical diameter greater than horizontal diameter	some apple varieties, capsicum, brinjal, rice, wheat
Conic	Tapered towered the apex	ladies finger, carrot, reddish
Ovate	Egg shaped & broad at stem end	Brinjal, apple and guava.
Oblique	Axis connecting stem and apex slated	some apple varieties, tomato.
Obovate	Inverted ovate-broad at apex	Mango, papaya
Elliptical	Approaching ellipsoid	rice, wheat, pointed guard etc
Truncate	Having both hand squared or flattened	capsicum
Unequal	One half larger than the other	mango
Ribbed:	In cross section, sides are more or less angular	plantain, ladies finger
Regular	Horizontal section approaches a circle	orange, apple, guava etc
Irregular	Horizontal section dearth materially from a circle	mango, ladies finger, capsicum etc.

 

Roundness:  Roundness is a measure of sharpness of the corners of the solid

    \[Roundness = \frac{{{A_p}}}{{{A_c}}}\]

Where A_p = largest projected area of object in natural rest position                                                                                   

 A_c = Area of smallest circumscribing circle

 The object area in obtained by projection/tracing

 

\[Roundness = \frac{{ \sum \nolimits^ r}}{{NR}}\]                             

 r    = radius of curvature of all the corners

R   = Radius of maximum inscribed circle

N   = total number of corners

 \[Roundnessratio = \frac{{{r_n}}}{{{R_m}}}\]

R_m = mean radius of the object

r_n   = radius of curvature of the sharpest corner

 

Sphericity:  Sphericity is the degree to Which an object resembles a sphere. The geometric foundation of the concept of sphericity

rests upon the isoperimetric property of a sphere. Sphericity can be expressed as:

\[Sphericity = \frac{{{d_i}}}{{{d_c}}}\]

d_i = diameter of largest inscribed circle

d_c = diameter of smallest circumscribed circle

A particle three dimensional expression can be stated for estimating the sphericity of an object using the following definition:

\[Sphericity = \frac{{{d_e}}}{{{d_c}}}\]

Where d_e is the diameter of the sphere of the same volume as the object and d_c is the diameter of the smallest circumscribed sphere or usually the longest diameter of the object. This expression for sphericity expresses the shape character of the solid relative to that of a sphere of the same volume.

Assuming that the volume of the solid is equal to the volume of a triaxial ellipsoid with intercepts a, b, c and that the diameter of the circumscribed sphere is the longest intercept of ellipsoid, the degree of sphericity can also be expressed.

d_e = diameter of sphere of the same volume of the object

d_c = diameter of the smallest circumscribing circle, usually the largest diameter of the object

\[Sphericity = {\left[ {\frac{{volumeofsolid}}{{volumeofcircumscribedsphere}}} \right]^{\frac{1}{3}}}\]

\[ = {\left[ {\frac{{\frac{\pi }{6}abc}}{{\frac{\pi }{6}{a^3}}}} \right]^{\frac{1}{3}}} = {\left[ {\frac{{bc}}{{{a^2}}}} \right]^{\frac{1}{3}}} = \frac{{{{\left[ {abc} \right]}^{\frac{1}{3}}}}}{a}\]

a= largest intercept

b = longest intercept normal to a

c = longest intercept normal to a and b

Resemblance to geometric bodies

In some cases the shape can be approximated by one of the following geometric shapes:

 

Prolate spheroid which is formed when an ellipse rotates about its major axis.        A prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter.  e.g. lemon, lime, grape
Oblate spheroid is formed when an ellipse rotates about its minor axis. An oblate spheroid is a rotationally symmetric ellipsoid having a polar axis shorter than the diameter of the equatorial circle whose plane bisects it. e.g. grape fruit, pumpkin   Right circular cone or cylinders is formed when a frustum rotates about its axis e.g. carrot and cucumber.

After deciding on the shape of body, its volume and surface area can be calculated using the appropriate equations. For some agricultural products, the following formulas may be applicable. Volume, V, and surface area, S, of prolate spheroid are given by:

\[{V_{prolatespheroid}} = \frac{4}{3}\pi a{b^2}\]

\[{S_{prolatespheroid}} = 2\pi {b^2} + 2\pi \frac{{ab}}{e}{\sin ^{ - 1}}e\]  

a = major semi axis of the ellipse

b = major semi axis of the ellipse

 \[where,e = ([1 - {(b/a)^2}])\]

Volume and Surface area of oblate spheroid are given by following expressions

\[{V_{oblatespheroid}} = \frac{4}{3}\pi {a^2}b\]

\[{S_{oblatespheroid}} = 2\pi {a^2} + \pi \frac{{{b^2}}}{e}\ln \frac{{1 + e}}{{1 - e}}\]

Volume, V, and surface area of the frustum of a right circular cone are given by

\[{V_{rightcone}} = \frac{\pi }{3}h[r_1^2 + {r_1}{r_2} + r_2^2]\]

\[{S_{rightcone}} = \pi \left( {{r_1} + {r_2}} \right)\sqrt {\left[ {{h^2} + {{\left( {{r_1} - {r_2}} \right)}^2}} \right]}\]

 r₁ = radius of base

r₂ = radius of top (apex)

h = altitude

Having volume and surface area estimated in this manner, the actual volume and surface area can then be determined experimentally and a correction factor can be established for the “typical” shape of each variety of the product

Some of the interrelations between major dimensions of the ellipsoid give an idea of the shape of the object such as slenderness ratio which is usually used for grading rice.

Length : width=Slenderness ratio

Width: length = aspect ratio

Fruit size can be expressed in terms of major diameter, minor diameter and length.

Ellipsoid ratio = Major diameter: minor diameter 

Aspect ratio= length: major diameter

 

Selected references:

Mohsenin, N.N. 1986. Physical Properties of Plant and Animal Materials, 2nd ed.; Gordon and Breach Science Publishers: New York

Moreda, G.P., Ortiz-Cañavate, J., García-Ramos, F.J. & Ruiz-Altisent, M. (2009). Non-destructive technologies for fruit and vegetable size determination – a review. Journal of Food Engineering 92 119–136

Sahin S. & Sumnu, S. G. 2006. Physical Properties of Foods. Springer, USA