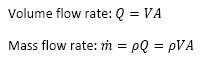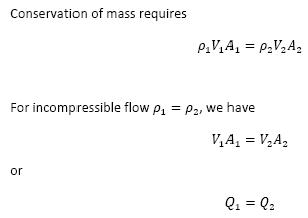Fluid Mechanics 3(2+1)

LESSON 19. APPLICATIONS OF BERNOULI’S EQUATION

• This principle results from a general integration of the equations of motion for an object in a very similar to that done for the fluid particle.

• With certain assumptions, a statement of the work-energy principle may be written as follows:

• The work done on a particle by all forces acting on the particle is equal to the change of the kinetic energy of the particle.

• The Bernoulli equation is a mathematical statement of this principle.

• In fact, an alternate method of deriving the Bernoulli equation is to use the first and second laws of thermodynamics (the energy and entropy equations), rather than Newton’s second law. With the approach restrictions, the general energy equation reduces to the Bernoulli equation.

 An alternate but equivalent form of the Bernoulli equation is:

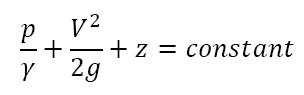
Along a streamline:

Pressure head:

Velocity head:

Elevation head:

Z

The Bernoulli equation states that the sum of the pressure head, the velocity head, and the elevation head is constant along a streamline.

Static, Stagnation, Dynamic, and Total Pressure

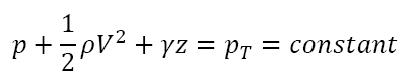
Along a streamline:

Static pressure:

ρ

Dynamic pressure:

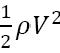
Hydrostatic pressure:

Y^_Z

 

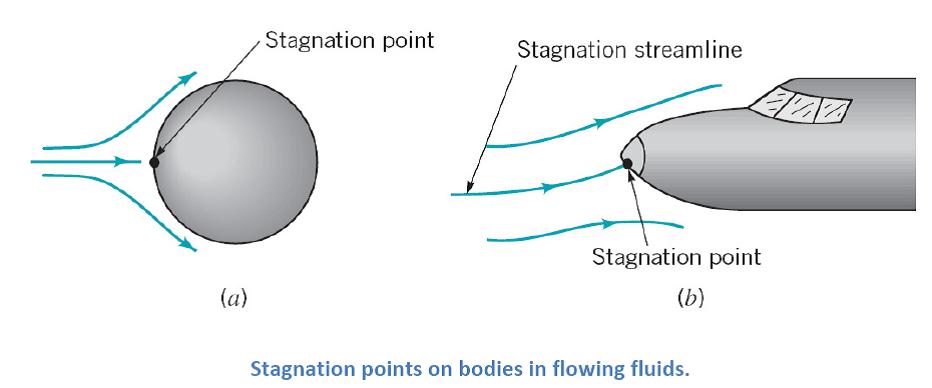
Stagnation pressure:

(assuming elevation effects are negligible) where p and V are the pressure and velocity of the fluid upstream of stagnation point. At stagnation point, fluid velocity V becomes zero and all of the kinetic energy converts into a pressure rise.

Total pressure:

(along a streamline)

Applications of Bernoulli Equation

1) Stagnation Tube

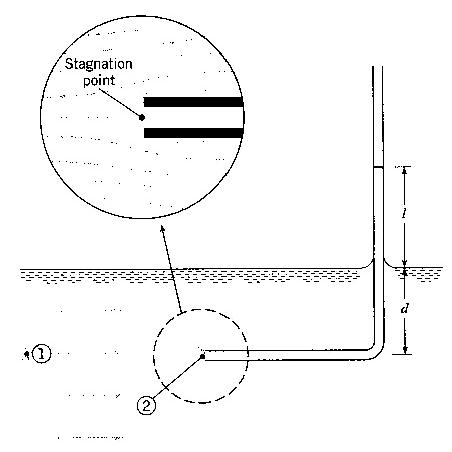
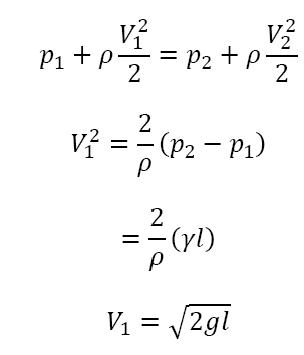
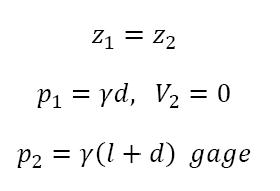
Limited by length of tube and need for free surface reference

2) Pitot Tube

 

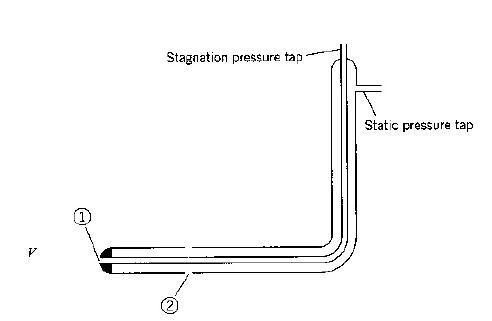
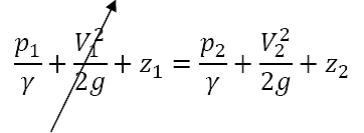
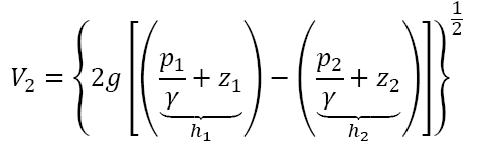
where,

V_{1 = 0 and h = piezometric head}

 

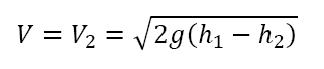
h1 - h2

from manometer or pressure gage

For gas flow

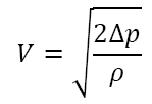
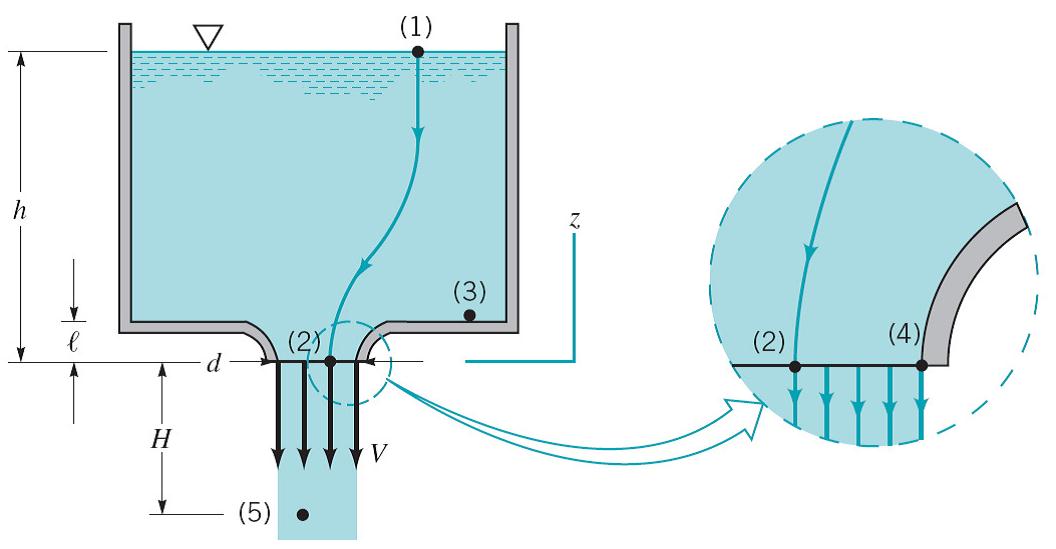
Application of Bernoulli equation between points (1) and (2) on the streamline

shown gives

Bernoulli equation between points (1) and (5) gives

 3) Simplified form of the continuity equation

 

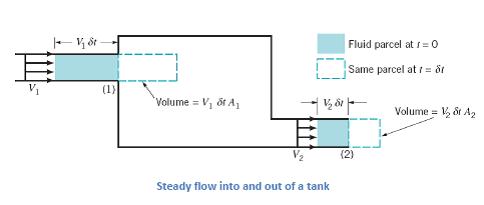
Obtained from the following intuitive arguments: