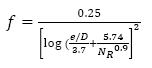LESSON 25. GENERAL EQUATION FOR HEAD LOSS-DARCY EQUATION

Flow of fluid through a pipe

  • Head loss is the reduction in the total head or pressure (sum of elevation head, velocity head and pressure head) of the fluid as it moves through a fluid system.

  •  Head loss is unavoidable in real fluids. It is present because of:

    • the friction between the fluid and the walls of the pipe;

    • the friction between adjacent fluid particles as they move relative to one another; and

    • the turbulence caused whenever the flow is redirected or affected in any way by such components as piping entrances and exits, pumps, valves, flow reducers, and fittings.

  • Frictional loss is that part of the total head loss that occurs as the fluid flows through straight pipes.

  • The head loss for fluid flow is directly proportional to the length of pipe, the square of the fluid velocity, and a term accounting for fluid friction called the friction factor.

  • The head loss is inversely proportional to the diameter of the pipe.

 Pressure Pipe Flow

 Refers to full water flow in closed conduits of circular cross sections under a certain pressure gradient. For a given discharge (Q), pipe flow at any location can be described by the pipe cross section, the pipe elevation, the pressure, and the flow velocity in the pipe.

Elevation (h)

of a particular section in the pipe is usually measured with respect to a horizontal reference datum such as mean sea level (MSL).

Pressure (P)

in the pipe varies from one point to another, but a mean value is normally used at a given cross section.

Mean velocity (V)

 is defined as the discharge (Q) divided by the cross-sectional area (A)

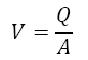
Module 16 Lesson 25 Pressure Pipe Flow

Loss of Head From Pipe Friction

Energy loss resulting from friction in a pipeline is commonly termed the friction head loss(hf). This is the loss of head caused by pipe wall friction and the viscous dissipation in flowing water. It is also called major loss.

The most popular pipe flow equation was derived by Henry Darcy (1803 to 1858), Julius Weiscbach (1806 to 1871), and the others about the middle of the nineteenth century. The equation takes the following form and is commonly known as the

Darcy-Weisbach Equation.

Module 16 Lesson 25 DARCY-WEISBACH EQUATION

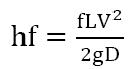
When Reynolds Number (NR) is less than 2000 flow in the pipe is laminar and friction factor is calculated with the following formula;

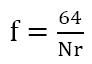
Module 16 Lesson 25 1.1 DARCY-WEISBACH EQUATION

When Reynolds Number (NR) is greater or equal to 2000, the flow in the pipe becomes practically turbulent and the value of friction factor (f) then becomes less dependent on the Reynolds Number but more dependent on the relative rougness (e/D) of the pipe. The roughness height for certain common commercial pipe materials is provided in Table 1.1.

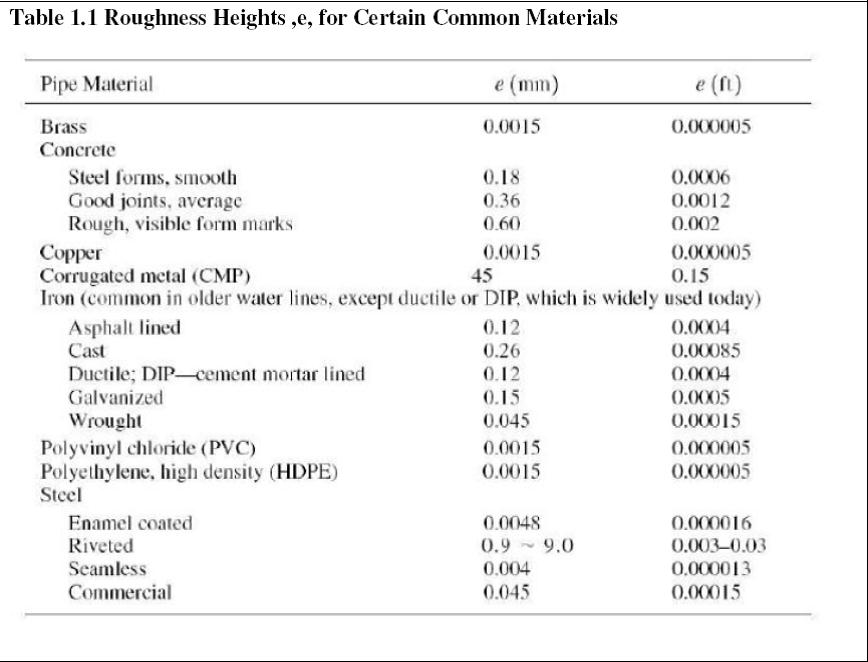
Module 16 Lesson 25 Table DARCY-WEISBACH EQUATION

Friction factor can be found in three ways:

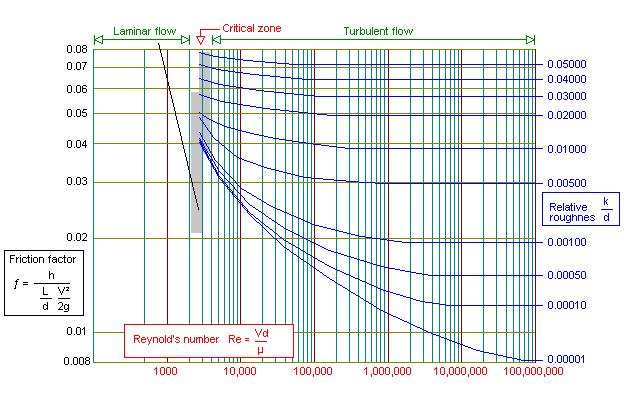
1. Graphical solution: Moody Diagram

2. Implicit equations : Colebrook-White Equation

3. Explicit equations: : Swamee-Jain Equation

1. Graphical solution: Moody Diagram

 Module 16 Lesson 25 GRAPHICAL SOLUTION MOODY DIAGRAM

2. Implicit equations : Colebrook-White Equation

Module 16 Lesson 25 2. IMPLICIT EQUATIONS COLEBROOK-WHITE EQUATION

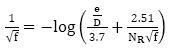
3. Explicit equations  : Swamee-Jain Equation

Module 16 Lesson 25 3. EXPLICIT EQUATIONS SWAMEE-JAIN EQUATION

Last modified: Tuesday, 8 October 2013, 9:52 AM