LESSON 12. Star- Delta conversion solution of DC circuit by Network theorems

12.1. Star Delta Transformation

In the complicated networks involving large number of resistances/ Kirchhoff’s Laws give us complex set of simultaneous equations. It is time consuming to solve such set of simultaneous equations involving large number of unknowns. In such a case application of Star-Delta or Delta-Star transformation, considerably reduces the complexity of the network and brings the network into a very simple form. This reduces the number of unknowns and hence network can be analyzed very quickly for the required result. These transformations allow us to replace three star connected resistances of the network, by equivalent delta connected resistances, without affecting currents in other branches and vice-versa.

Standard 3-phase circuits or networks take on two major forms with names that represent the way in which the resistances are connected, a Star connected network which has the symbol of the letter, Υ (wye) and a Delta connected network which has the symbol of a triangle, Δ (delta). If a 3-phase, 3-wire supply or even a 3-phase load is connected in one type of configuration, it can be easily transformed or changed it into an equivalent configuration of the other type by using either the Star Delta Transformation or Delta Star Transformation process.

A resistive network consisting of three impedances can be connected together to form a T or "Tee" configuration but the network can also be redrawn to form a Star or Υ type network as shown below.

12.2. T-connected and Equivalent Star Network

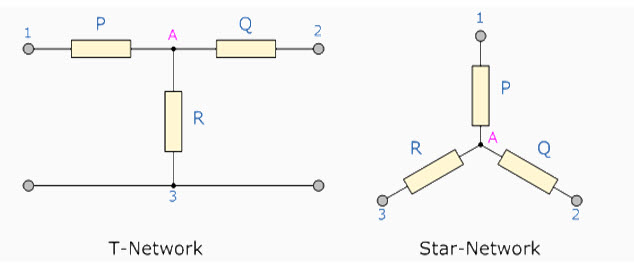
Module 1 Lesson 12 Fig.12.1

Fig. 12.1

As we have already seen, we can redraw the T resistor network to produce an equivalent Star or Υ type network. But we can also convert a Pi or π type resistor network into an equivalent Delta or Δ type network as shown below.

12.3. Pi-connected and Equivalent Delta Network.

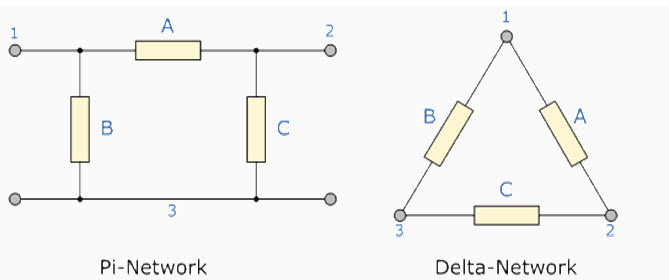
Module 1 Lesson 12 Fig.12.2

Fig. 12.2

Having now defined exactly what is a Star and Delta connected network it is possible to transform the Υ into an equivalent Δ circuit and also to convert a Δ into an equivalent Υ circuit using a the transformation process. This process allows us to produce a mathematical relationship between the various resistors giving us a Star Delta Transformation as well as a Delta Star Transformation.

These transformations allow us to change the three connected resistances by their equivalents measured between the terminals 1-2, 1-3 or 2-3 for either a star or delta connected circuit. However, the resulting networks are only equivalent for voltages and currents external to the star or delta networks, as internally the voltages and currents are different but each network will consume the same amount of power and have the same power factor to each other.

12.4. Delta Star Transformation

To convert a delta network to an equivalent star network we need to derive a transformation formula for equating the various resistors to each other between the various terminals. Consider the circuit below

12.4.1. Delta to Star Network.

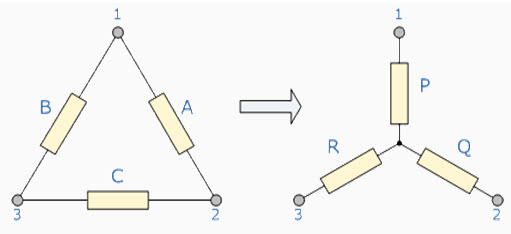
Module 1 Lesson 12 Fig.12.3

 Fig. 12.3

Compare the resistances between terminals 1 and 2.

\[P-Q=A in parallel with\left( {B - C} \right)\]

\[P - Q={{A\left({B + C}\right)} \over {A + B + C}}..............\left( {EQ1} \right)\]

Resistance between the terminals 2 and 3.

\[Q - R=Cinparallelwith\left( {A - B} \right)\]

\[Q - R={{C\left( {A + B} \right)} \over {A + B + C}}........................\left( {EQ2}\right)\]

Resistance between the terminals 1 and 3.

\[P - R=Binparallelwith\left( {A - C} \right)\]

\[P - R={{B\left( {A + C} \right)} \over {A + B + C}}......................\left( {EQ3} \right)\]

This now gives us three equations and taking equation 3 from equation 2 gives:

\[EQ3 - EQ2=\left( {P - R} \right) - \left( {Q + R} \right)\]

\[P + R={{B\left( {A + C} \right)} \over {A + B + C}} + Q - R={{C\left( {A + B} \right)}\over {A + B + C}}\]

\[P - Q={{BA - CB} \over {A + B + C}} - {{CA + CB} \over {A + B + C}}\]

\[P - Q={{BA - CA} \over {A + B + C}}\]

Then, re-writing Equation 1 will give us:

\[P + Q={{AB - AC} \over {A + B + C}}\]

Adding together equation 1 and the result above of equation 3 minus equation 2 gives:

\[\left( {P - Q} \right) + \left( {P + Q} \right)={{BA - CA} \over {A + B + C}} + {{AB - AC} \over {A + B + C}}\]

\[=2P={{2AB} \over {A + B + C}}\]

From which gives us the final equation for resistor P as:

\[P={{AB} \over {A + B + C}}\]

Then to summarize a little the above maths, we can now say that resistor P in a Star network can be found as Equation 1 plus (Equation 3 minus Equation 2) or   Eq1 + (Eq3 - Eq2).

Similarly, to find resistor Q in a star network, is equation 2 plus the result of equation 1 minus equation 3 or Eq2 + (Eq1 - Eq3) and this gives us the transformation of Q as:

\[Q={{AC} \over {A + B + C}}\]

and again, to find resistor R in a Star network, is equation 3 plus the result of equation 2 minus equation 1 or  Eq3 + (Eq2 - Eq1) and this gives us the transformation of R as:

\[R={{BC} \over {A + B + C}}\]

When converting a delta network into a star network the denominators of all of the transformation formulas are the same: A + B + C, and which is the sum of ALL the delta resistances. Then to convert any delta connected network to an equivalent star network we can summarized the above transformation equations as:

\[P={{AB} \over {A + B + C}}\]

\[Q={{AC} \over {A + B + C}}\]

\[R={{BC} \over {A + B + C}}\]

Last modified: Thursday, 26 September 2013, 5:04 AM