Site pages
Current course
Participants
General
Module 1. Average and effective value of sinusoida...
Module 2. Independent and dependent sources, loop ...
Module 3. Node voltage and node equations (Nodal v...
Module 4. Network theorems Thevenin’ s, Norton’ s,...
Module 5. Reciprocity and Maximum power transfer
Module 6. Star- Delta conversion solution of DC ci...
Module 7. Sinusoidal steady state response of circ...
Module 8. Instantaneous and average power, power f...
Module 9. Concept and analysis of balanced polypha...
Module 10. Laplace transform method of finding ste...
Module 11. Series and parallel resonance
Module 12. Classification of filters
Module 13. Constant-k, m-derived, terminating half...
LESSON 13. Delta to Star Transformations solution of DC circuit by Network theorems
13.1. Delta to Star Transformations Equations are
\[P={{AB} \over {A + B + C}}\]
\[Q={{AC} \over {A + B + C}}\]
\[R={{BC} \over {A + B + C}}\]
If the three resistors in the delta network are all equal in value then the resultant resistors in the equivalent star network will be equal to one third the value of the delta resistors, giving each branch in the star network as: RSTAR = 1/3RDELTA
Example No1
Convert the following Delta Resistive Network into an equivalent Star Network.
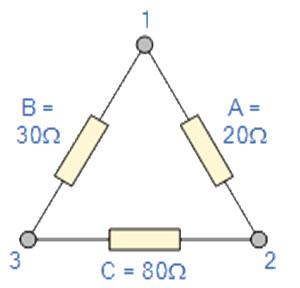
\[Q={{AC} \over {A + B + C}}\]
\[Q={{20x80} \over {20 + 30 + 80}}\]
\[Q=12.31\Omega\]
\[P={{AB} \over {A + B + C}}\]
\[P={{20x30} \over {20 + 30 + 80}}\]
\[P=4.61\Omega\]
\[R={{BC} \over {A + B + C}}\]
\[R={{30x80} \over {20 + 30 + 80}}\]
\[R=18.46\Omega\]
13.2. Star Delta Transformation
We have seen above that when converting from a delta network to an equivalent star network that the resistor connected to one terminal is the product of the two delta resistances connected to the same terminal, for example resistor P is the product of resistors A and B connected to terminal 1. By rewriting the previous formulas a little we can also find the transformation formulas for converting a resistive star network to an equivalent delta network giving us a way of producing a star delta transformation as shown below.
13.2.1. Star to Delta Network.
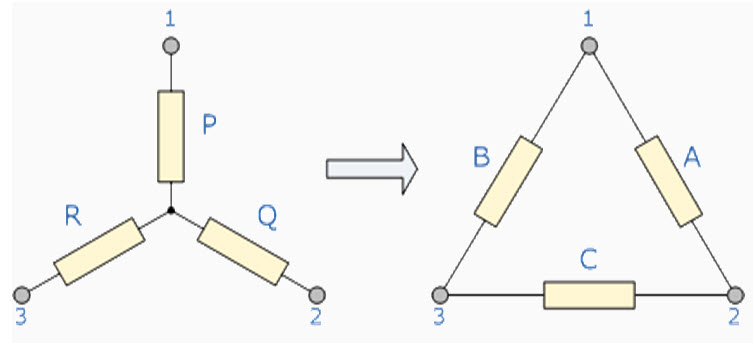
The value of the resistor on any one side of the delta, Δ network is the sum of all the two-product combinations of resistors in the star network divide by the star resistor located "directly opposite" the delta resistor being found. For example, resistor A is given as:
\[A={{PQ + QR + RP} \over R}\]
with respect to terminal 3 and resisor B is given as:
\[B={{PQ + QR + RP} \over Q}\]
with respect to terminal 2 with resistor C given as:
\[C={{PQ + QR + RP} \over P}\]
with respect to terminal 1.
By dividing out each equation by the value of the denominator we end up with three separate transformation formulas that can be used to convert any Delta resistive network into an equivalent star network as given below.
13.2.2. Star Delta Transformation Equations are
\[A={{PQ} \over R} + Q + P\]
\[B={{RP} \over Q} + P + R\]
\[C={{QR} \over P} + Q + R\]
Star Delta Transformations allow us to convert one circuit type of circuit connection to another in order for us to easily analyze a circuit and one final point about converting a star resistive network to an equivalent delta network. If all the resistors in the star network are all equal in value then the resultant resistors in the equivalent delta network will be three times the value of the star resistors and equal, giving: RDELTA = 3RSTAR