Electrical Circuits 3(2+1)

LESSON 29. Classification of pass Band and Stop Band

We known that the propagation constant is a complex function \[\gamma\] = \[\alpha\] + jβ, the real part of the complex propagation constant \[\alpha\] , is a measure of the change in magnitude of the current or voltage in the network, known as the attenuation constant.  β is a measure of the difference in phase between the input and output currents or voltages, known as phase shift constant.  Therefore \[\alpha\] and β take on different values depending upon the range of Z₁/4Z₂, From Eq. 28.7, we have

\[\sinh {\gamma  \over 2}=\,\sinh \left( {{\alpha\over 2} + {{j\beta} \over 2}} \right)=\sinh {\alpha\over 2}\cos {\beta\over 2} + \,\,j\,\,\cosh {\alpha\over 2}\sin {\beta\over 2}\]

\[=\sqrt {{{{Z_1}} \over {4{Z_2}}}} ...................................................\left( {29.1} \right)\]

Case A

If Z₁ and Z₂ are the same type of reactances, then \[\left[ {{{{Z_1}} \over {4{Z_2}}}} \right]\] is real and equal to say a+x,

The imaginary part of the Eq. 29.1 must be zero.

\[\cosh \,{\alpha\over 2}\sin {\beta\over 2}=0...................................................\left( {29.2} \right)\]

\[\sinh \,{\alpha\over 2}\cos {\beta\over 2}=x...................................................\left( {29.3} \right)\]

\[\alpha\] and β must satisfy both the above equations.

Equation 29.2 can be satisfied if β/2 = 0 or n\[\pi\], where n = 0, 1,2,…, then cos β/2 = 1 and sinh

\[\alpha /2=x=\sqrt {{{{Z_1}} \over {4{Z_2}}}}\]

That x should be always positive implies that

\[\sqrt {{{{Z_1}} \over {4{Z_2}}}}>0\,and\,\alpha=2\,{\sinh ^{-1}}\sqrt {{{Z_1^{}} \over {4{Z_2}}}} ...................................................\left( {29.4} \right)\]

Since \[\alpha\]  ≠ 0, it indicates that the attenuation exists.

Case B

Consider the case of Z₁ and Z₂ being appositive type of reactances, i.e. Z₁/4Z₂ is negatie, making \[\sqrt {{Z_1}/4{Z_2}}\] imaginary and equal to say jx

The real part of the Eq.29.1 must be zero.

\[\sinh \,{\alpha\over 2}\cos {\beta\over 2}=0...................................................\left( {29.5} \right)\]

\[\cosh \,{\alpha\over 2}\sin {\beta\over 2}=x...................................................\left( {29.6} \right)\]

(i) When \[\alpha\] = 0; from Eq. 29.5, sinh \[\alpha\]/2 = 0.  And from Eq.29.6 sin \[\beta /2=x=\sqrt {{Z_1}/4{Z_2}}\] .  But the sine can have a maximum value of 1.  Therefore, the above solution is valid only for negative Z₁/4Z₂, and having maximum value of unity.  It indicates the conduction of pass band with zero attenuation and follows the condition as

\[- 1 \le {{{Z_1}} \over {4{Z_2}}} \le 0\]

\[\beta=2{\sin ^{-1}}\sqrt {{{{Z_1}} \over {4{Z_2}}}} ...................................................\left( {29.7} \right)\]

(ii) When β = \[\pi\], from Eq.29.5, cos β/2 = .  And from Eq.29.6, sinβ/2 = ±1;

cosh a2 = \[x=\sqrt {{Z_1}/4{Z_2}}\] .

Since cosh \[\alpha\]/2 ≥ 1, this solution is valid for negative Z₁/4Z₂, and having magnitude greater than, or equal to unity.  It indicates the condition of stop band since \[\alpha\] = 0.

\[-\alpha\le {{{Z_1}} \over {4{Z_2}}} \le-1\]

\[\alpha=2{\cos ^{-1}}\sqrt {{{{Z_1}} \over {4{Z_2}}}} ...................................................\left( {29.8} \right)\]

It can be observed that there are three limits for case A and B.  Knowing the values of Z1 and Z2, it is possible to determine the case to be applied to the filter.  Z1 and Z2 are made of different types of reactances, or combinations of reactances, so that, as the frequency changes, a filter may pass from one case to another.  Case A and (ii) in case B are attenuation bands, whereas (i) in case B is the transmission band.

The frequency which separates the attenuation band from pass band or vice versa is called cut-off frequency.  The cut-off frequency is denoted by ƒ_c,  and is also termed as nominal frequency.  Since Z₀ is real in the pass band and imaginary in an attenuation band, ƒ_c is the frequency at which Z₀ cahnges from being real to being imaginary.  These frequencies occur at

\[{{{Z_1}} \over {4{Z_2}}}=0\,\,or\,\,{Z_1}=0...................................................\left( {29.8a} \right)\]

\[{{{Z_1}} \over {4{Z_2}}}=1\,\,or\,\,{Z_1} + 4{Z_2}=0...................................................\left( {29.8b} \right)\]

The above conditions can be represented graphically, as in Fig. 29.1

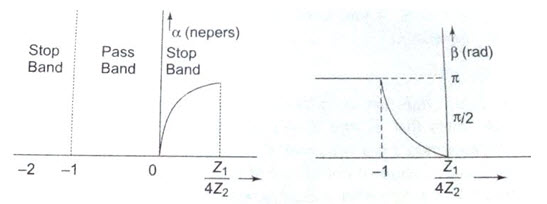
Fig.29.1

29.2. Characteristic Impedance in the Pass and Stop Bands

Referring to the characteristic impedance of a symmetrical T-network, from Eq.28.1 we have

                       \[{Z_{0T}}=\sqrt {{{Z_1^2} \over 4} + {Z_1}{Z_2}}=\sqrt {{Z_1}{Z_2}\left( {1 + {{{Z_1}} \over {4{Z_2}}}} \right)}\]

If Z₁ and Z₂ are purely reactive, let Z₁ = jx₁ and Z₂ = jx₂, then

                       \[{Z_{0T}}=\sqrt {{x_1}{x_2}\left( {1 + {{{Z_1}} \over {4{Z_2}}}} \right)} ...................................................\left( {29.9} \right)\]

A pass band exists when x₁ and x₂ are of opposite reactance and

                      \[-1 < {{{x_1}} \over {4{x_2}}} < 0\]

Substituting these conditions in Eq.29.9, we find that Z_0T is positive and real.  Now consider the stop band.  A stop band exists when x₁ and x₂ are of the same type of reactances; then x₁/4x₂ > 0.  Substituting these conditions in Eq.29.9, we find that Z_OT is purely imaginary in this attenuation region.  Another stop band exists when x₁ and x₂ are of the same type of reactances, but with x₁/4x₂ < -1.  Then from Eq.29.9, Z_0T is again purely imaginary in the attenuation region.

Thus, in a pass band if a network is terminated in a pure resistance R₀ (Z_0T = R₀), the input impedance is R₀ and the network transmits the power received from the source to the R₀ without any attenuation. In a stop band Z_0T is reactive.  Therefore, if the network is terminated in a pure reactance (Z₀ = pure reactance), the input impedance is reactive, and cannot receiver or transmit power.  However, the network transmits voltage and current with 90⁰ phase difference and with attenuation.  It has already been shown that the characteristic impedance of a symmetrical p-section can be expressed in terms of T.  Thus, from Eq.29.9,

Z_0p = Z₁Z₂/Z_0T.

Since Z₁ and Z₂ are purely reactive, Z_0\[\pi\] is real if Z_0T is real, and Z_0x is imaginary if Z_0T is imaginary.  Thus the conditions developed for T = sections are valid for \[\pi\] sections.