Strength of Material

LESSON 22. Columns and Struts

22.2 Euler Load for Columns with Pinned End

Assumptions

• Member is prismatic and perfectly straight.

• The material is homogeneous and linear elastic.

• One end of the member is hinged and the other is restrained against horizontal movement as shown in Figure 22.2a.

• The compressive load is acting along the longitudinal axis of the member.

• Lateral deformation of the member is small.

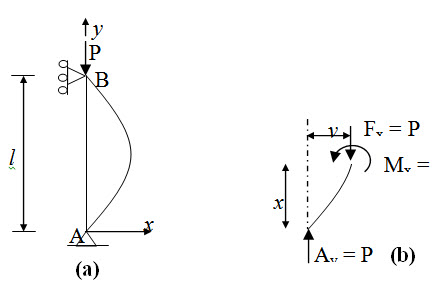Fig. 22.2.

From equation of elastic line (lesson 3), we have,.

\[{{{d^2}y} \over {d{x^2}}}=-{{{M_x}} \over {EI}}\]                                                             (22.1)

\[\Rightarrow {{{d^2}y} \over {d{x^2}}} + {P \over {EI}}y = 0\]                                            (22.2)

Equation (22.2) is a second order linear differential equation with constant coefficients. Boundary conditions are,

\[y(x = 0) = y(x = l) = 0\]              (22.3)

Equations (22.2) – (22.3) define a linear eigenvalue problem, whose solution may be written as,

\[y = A\cos kx + B\sin kx\]            (22.4)

where, \[{k^2} = {P / {EI}}\] . Constants A and B may be determined from the boundary conditions (Equation 22.3),

Imposing y(x = 0) = 0 we have A = 0.

Imposing y(x = l) = 0 we have,

\[B\sin kl = 0\]                                (22.5)

As B ≠ 0 , \[\sin kl = 0 \Rightarrow kl = n\pi \]

where,

Hence,

\[{k^2} = {P \over {EI}} = {{{n^2}{\pi ^2}} \over {{l^2}}}\]

\[\Rightarrow {P_{crn}} = {{{n^2}{\pi ^2}} \over {{l^2}}}EI\]                                                (22.6)

The eigenvalues \[{P_{crn}}\]  are the critical loads at which buckling takes place in different modes which are given by,

\[y = B\sin {{n\pi x} \over l}\]      (22.7)

The smallest Euler buckling load is (n = 1),

\[{P_E} = {{{\pi ^2}EI} \over {{l^2}}}\]                                                                                        (22.8)

22.3 Euler Load for Columns with Different End Conditions

Equation (22.8) may be recast as,

\[{P_E} = {{{\pi ^2}EI} \over {l_{eff}^2}}\]                                                                                 (22.8)

where, l_eff is the effective length of the column. For column with both ends hinged, l_eff = l. Different end condition may increase or decrease the effective length and consequently change the critical buckling load. Effective lengths of column with different end conditions are given below.

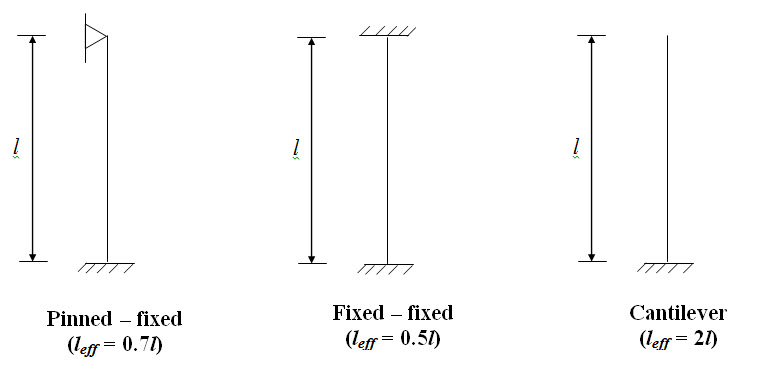Fig. 22.3.

 

 

Suggested Readings

Yoo, C.H., Lee, S.C. (2011). Stability of Structures: Principles and Applications. Elsevier. 

Gere, J.M, Timoshenko S.P. (2010). Theory of Elastic Stability. Second Edition, Tata McGraw - Hill Education.