Engineering Mechanics

LESSON 2. FORCE SYSTEM

2.2 CHARACTERISTICS OF A FORCE

 A Force has following basic characteristics

i) Magnitude                              

ii) Direction

iii) Point of application

iv) Line of action

Force is represented as a vector .i.e an arrow with its magnitude.

e.g. for the force shown in Fig. 2.1, magnitude of force is 4KN, direction is 40° with the horizontal in fourth quadrant, point of application is C and line of action is AB.

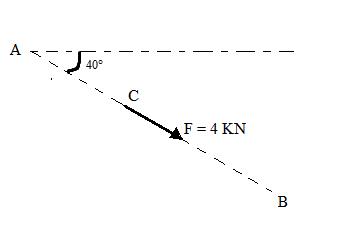
Fig.2.1 Characteristics of a force

 Smaller magnitudes of forces are measured in newton (N) and larger in kilonewton (KN).

2.3 SYSTEMS OF FORCES                         

 When a mechanics problem or system has more than one force acting, it is known as a ‘force system’ or ‘system of force’.

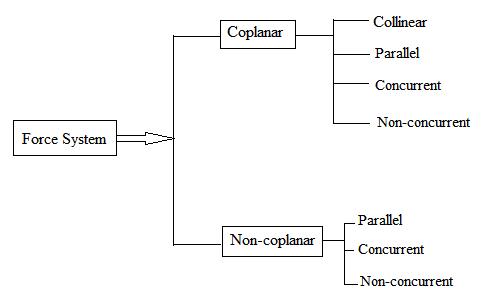
Fig.2.2 Force System

2.3.1 Collinear Force System

When the lines of action of all the forces of a system act along the same line, this force system is called collinear force system.

 

Fig.2.3 Force System

2.3.2 Parallel Forces

 

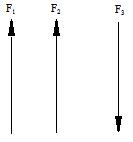
Fig.2.4 Force System

 

2.3.3 Coplanar Force System

When the lines of action of a set of forces lie in a single plane is called coplanar force system.

2.3.4 Non-Coplanar Force System

When the line of action of all the forces do not lie in one plane, is called Non-coplanar force system

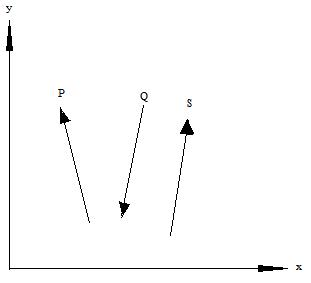
Fig.2.5 Force System

2.3.5 Concurrent Force System

The forces when extended pass through a single point and the point is called point of concurrency. The lines of actions of all forces meet at the point of concurrency. Concurrent forces may or may not be coplanar.

2.3.6 Non-concurrent Force System

When the forces of a system do not meet at a common point of concurrency, this type of force system is called non-concurrent force system. Parallel forces are the example of this type of force system. Non-concurrent forces may be coplanar or non-coplanar.

2.3.7 Coplanar and concurrent force system

A force system in which all the forces lie in a single plane and meet at one point, For example, forces acting at a joint of a roof truss (see fig.2.6)

P = External force

F₁ to F₅ = Member forces (internal) R_A and R_B = Reactions

C = Point of concurrency

 

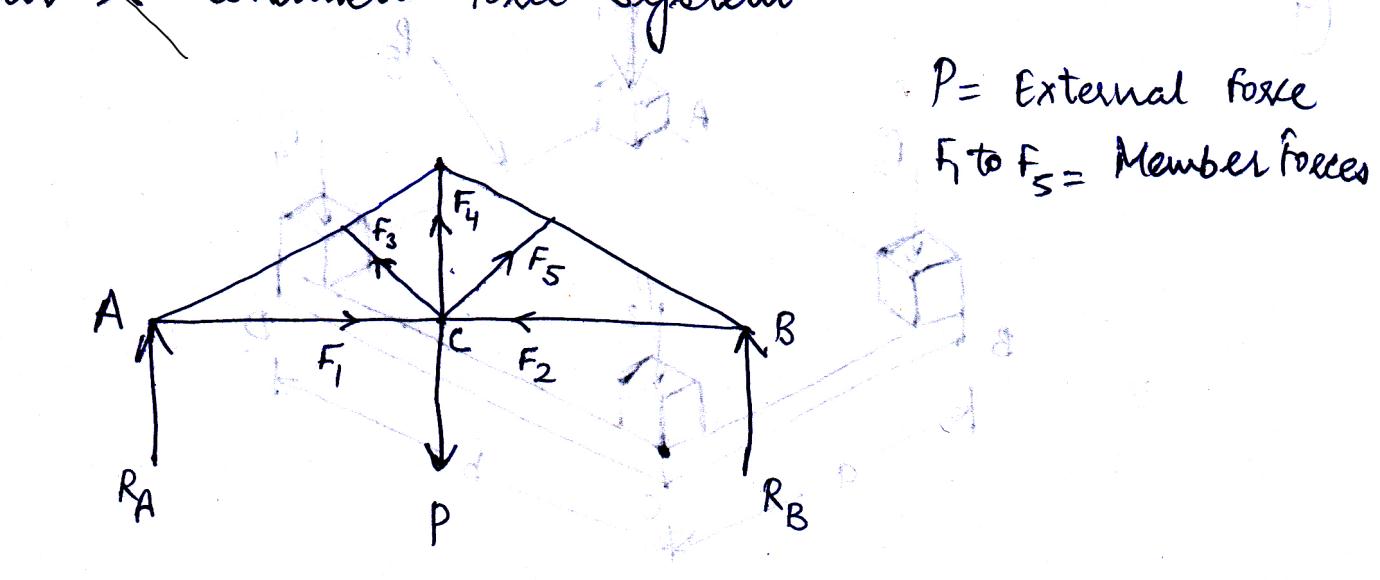
Fig.2.6 Coplanar concurrent force system

2.3.8 Coplanar and non-concurrent force system

These forces do not meet at a common point; however, they lie in a single plane, for example, forces acting on a beam as shown in Fig.2.7:

 

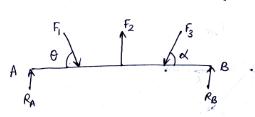
Fig.2.7 Coplanar non-concurrent force system

2.3.9 Non-coplanar and concurrent force system

In this system, the forces lie in a different planes but pass through a single point. Example is forces acting at the top end of an electrical pole (see Fig.2.8)

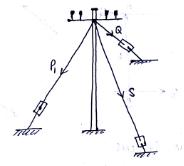
Fig.2.8 Force System

 Example 2.1: The tension in the guy wires OA and OB of the electrical pole are 500 N and 300 N respectively as shown in Fig.2.9. Determine the horizontal and vertical components of these tensions exerted by the guy wires on the pole at O.

Fig 2.9

Solution: The tensions exerted by the guy wires on the pole at O are acting as shown in the above figure. The components of each of the forces are determined as given in the following table:

Cable	Force P	Inclination with x-axis Ө	x-component Px = P cos Ө	y-component Py = P sin Ө
OB	500 N	tan-1 6/2 = 71.57°	500 cos 71.57° = 158.07 N (→)	500 sin 71.57° = 474.36 N (↓)
OA	300 N	tan-1 6/1.5 = 75.96°	300 cos 75.96° = 72.78 N (←)	300 sin 75.96° = 291.04 N (↓)

 

2.3.10 Non-coplanar and non-concurrent force system

The forces which do not lie in a single plane and do not pass through a single point are known as non-coplanar and non-concurrent forces. Example is the loads transferred through columns to the rectangular mat foundation as shown in Fig.2.10.

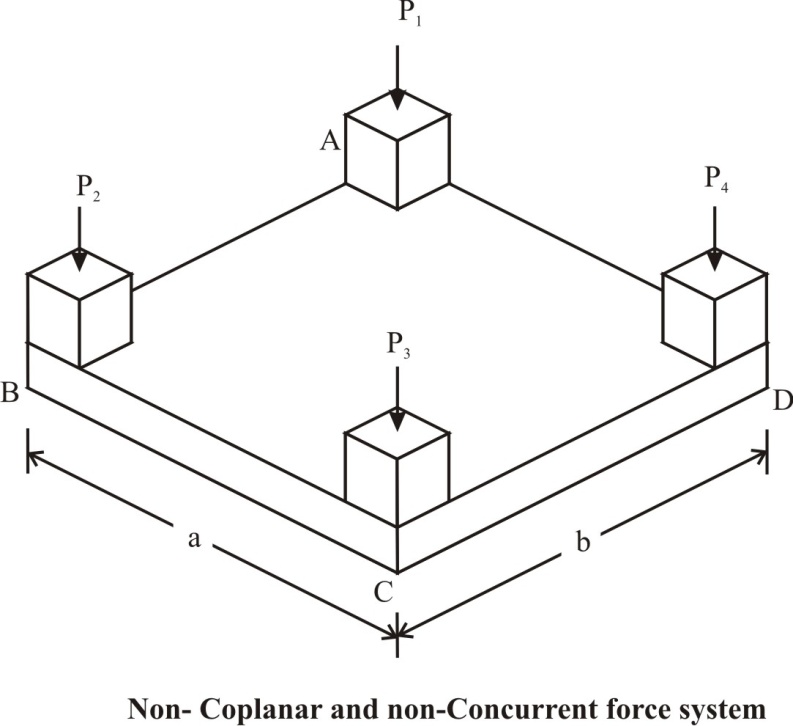
Fig. 2.10 Non-coplanar non-concurrent force system