LESSON 10. Triangular Area

Triangular Area

From Eq. (11.7), moment of inertia of a triangle about its base x-x as shown in Fig.12  is

                                                           Ix = \[{{b{d^3}} \over {12}}\]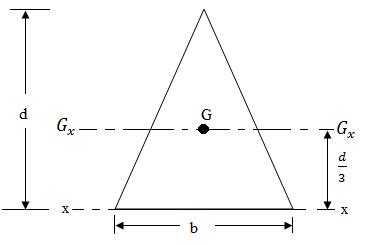
Module 3 Lesson 10 Fig.12 Moment of inertia of a triangle about its centroidal axis

 Fig.12 Moment of inertia of a triangle about its centroidal axis

The moment of inertia about centroidal axis is

IGx = Ix – Ah2 = Ah2 \[{{b{d^3}} \over {12}} - {{bd} \over 2}{\left( {{d \over 3}} \right)^3}\]

 IGx = \[{{b{d^3}} \over {36}}\]           (11.13)

Semicircular Area

Equation (11.9) gives the moment of inertia of semicircular area about x and y axes as given in Fig.13. That is

Ix = Iy = \[{{{R^4}} \over 8}\]

Fig.13 Moment of inertia of a semicircular about its centroidal axis

Module 3 Lesson 10 Fig.13 Moment of inertia of a semicircular about its centroidal axis

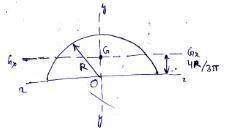
However, y-axis passes through the centroid G, hence, moment of inertia about centroidal y-axis is same as

                                                   IGy = Iy = \[{{{R^4}} \over 8}\]

Moment of inertia about centroidal x-axis is

IGx = Ix – Ah2 = \[{{{R^4}} \over 8} - {{{R^2}} \over 2}{\left( {{{4R} \over {3}}} \right)^2}\]

                                               IGx = 0.11R4                                                            (11.14)

 Quarter Circular Area

Moment of inertia of quarter circular area about x and y axes [Eq.(11.10)] as shown in Fig.14 is

 Ix = Iy = \[{{{R^4}} \over 16}\]

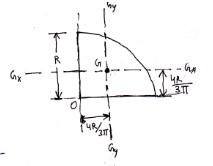
Module 3 Lesson 10 Fig.14 Moment of inertia of a quarter circle about its centroidal axis

Fig.14 Moment of inertia of a quarter circle about its centroidal axis

Therefore, moment of inertia about centroidal axes (Gx and Gy) is determined as

IGx = Ix – Ah2 = \[{{R^4}} \over {16}}\] - \[{{{R^2}} \over 4}{\left( {{{4R} \over {3}}} \right)^2}\]

IGx = 0.055R4                                                           (11.15a)

Similarly, IGy will be obtained and it is equal to IGx itself.

  IGy = 0.055R4                                                     (11.15b)

Moment of Inertia of hollow rectangular and circular sections about their centroidal axes are given in Fig.15.

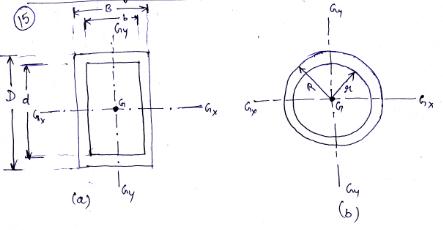
 Module 3 Lesson 10 Fig.15 (a) Hollow rectangular section and (b) Hollow circular section

  Fig.15 (a) Hollow rectangular section and (b) Hollow circular section

Hollow rectangular section:

                                             IGx = \[{1 \over {12}}\left( {B{D^3} - b{d^3}} \right)\]                                                     (11.16a)

                                            IGy =  \[{1 \over {12}}\left( {D{B^3} - d{b^3}} \right)\]                                                     (11.16b)

Hollow circular section:

                                             IGx = IGy =  \[{ \over 4}\left( {{R^4} - {r^4}} \right)\]                                                     (11.17)

 

Last modified: Tuesday, 10 September 2013, 5:48 AM