Site pages
Current course
Participants
General
Module 1. Tractor Mechanics
Module 2. Traction
Module 3. Introduction to Transmission System
Module 4. Clutch System
Module 5. Gear Box
Module 6. Differential and Final drive
Module 7. Brakes
Module 8. Steering system
Module 9. Hydraulics
Module 10. Power Transmission
Lesson 3. Determination and importance of Moment of Inertia of a tractor
Moments Of Inertia
Moment of inertia is the property of a distribution of mass in space that measures its resistance to rotational acceleration about an axis. The Newton’s first law can be extended in the terms that the inertia of a body that is rotating about an axis shall remain rotating unless acting upon by an external torque.
The moment of the inertia force on a particle around an axis multiplies the mass of the particle by the square of its distance to the axis, and forms a parameter called the moment of inertia. The moments of inertia of individual particles sum to define the moments of inertia of a body rotating about an axis.
Moment of inertia appears in Newton’s second law for the rotation of a rigid body, which states that the torque necessary to accelerate rotation is proportional to the moment of inertia of the body. Thus, the greater the moment of inertia the torque needed for the same acceleration.
The moment of inertia of an object is defined by the distribution of mass around an axis. It depends not only on the total mass of the object, but also on the square of the perpendicular distance from the axis to each each elements of mass. This means the moment of inertia increases rapidly as masses are distributed more distant from the axis.
Mass Moments of Inertia Determination: If the rotational motion of a tractor is being considered, it is necessary to know its mass moment of inertia about the axis of rotation in question. The tractor may rotate about any one of its three axes: longitudinal, transverse, and vertical. There are more sophisticated methods for determining the mass moment of inertia than the one presented here which is quite basic.
If a tractor is suspended from a hoist, as in fig.14.3, the tractor plus the sling will be a compound pendulum which will oscillate with a frequency of:

where I0 = the mass moment of inertia about the pivot
f = the frequency in cps
W = the weight in lb
r = the radius in feet from the center of gravity to the pivot point of the sling holding the tractor.
From equation 1everything can be measured except I0 which can then be computed. The moment of inertia with respect to the center of gravity, ICG, can then be computed as follows:
ICG = I0 – Wr2/g (2)
If English units of measurement are used, the dimensions of I will be in ft lb sec2.
It is, of course, possible, but not practical, to compute the mass moment of inertia thus:
![]()
If, however, it is to study the dynamic behavior of a tractor still in the drawing-board stage, it will be necessary to make an estimate of I by use of equation 3.
The pendulum method as described below can be readily used for determining the mass moment of inertia with respect to the transverse and longitudinal axes.
If a tractor in a cradle is suspended from a hoist (Fig. 2.1), the tractor plus the cradle will behave as a compound pendulum which will oscillate with a frequency of

Also the M.I. of cradle alone its axis of rotation is given by:

The M.I of tractor plus cradle about the exis of rotation is given by:

The radius of gyration ‘r’ is given by:
![]()
Finally the required M.I of tractor about its C.G. is
![]()
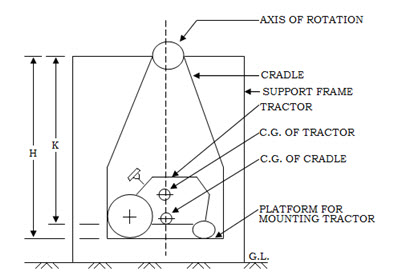
Fig. 2.1 Tractor mounted on cradle for determination of moment of inertia
Where:
|
M.I |
= |
Moment of inertia, Kg-cm-sec2 |
|
W |
= |
Weight of tractor + weight of cradle = Wt + WC, Kgf |
|
r |
= |
Distance of C.G. of cradle plus tractor from axis of rotation, cm |
|
Io |
= |
Mass moment of inertia of tractor and cradle about the axis of rotation of cradle, Kg-cm-sec2 |
|
fo |
= |
Frequency of oscillations of tractor plus cradle, cycles/sec |
|
f1 |
= |
Frequency of oscillations of cradle, cycles/sec |
|
Ic |
= |
Moment of inertia of cradle about axis of rotation, Kg-cm-sec2 |
|
IC.G. |
= |
Moment of inertia of tractor about the required axis through its centre of gravity, Kg-cm- sec2 |
|
X, Y |
= |
Location of centre of gravity of tractor in horizontal and vertical directions and from rear wheel axle and ground level respectively, cm |
|
H |
= |
Height of axis of rotation above platform, cm |
|
K |
= |
Height of axis of rotation above centre of gravity of cradle, cm |