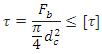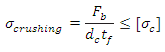Machine Design 3(2+1)

LESSON 16 DESIGN OF COUPLINGS

16.2          Types of Shafts Couplings

Rigid Couplings

Rigid Couplings are used to connect two shafts which are perfectly aligned. These are simple and inexpensive.

Rigid Couplings are of following types:

1. Sleeve or Muff Coupling
2. Clamp or Split-muff or Compression Coupling
3. Flange Coupling

Flexible Couplings

Flexible couplings are used to connect two shafts having lateral or angular misalignment. Flexible elements provided in flexible coupling absorb shocks and vibrations.

Flexible Couplings are of following types:

1. Bushed pin type Coupling
2. Universal Coupling
3. Oldham Coupling

16.3          Muff Coupling

16.3.1    Introduction

Assembly of muff coupling is shown in Figure 16.1. Sleeve, a hollow cylinder, is fitted on the ends of input and output shaft with the help of a sunk key. Torque is transmitted from input shaft to the sleeve through key and from the sleeve to the output shaft through the key again. It is simple to design and manufacture but difficult to assemble and dismantle. It requires more axial space and has small radial dimensions. Sleeve is made of cast iron and for it a larger factor of safety of 6-8 is used on the ultimate strength. Standard proportions used for sleeve are:

Outer diameter of the sleeve,             D = 2d + 13

Length of the sleeve,                         L = 3.5d

where d is the diameter of the shaft.

So the muff coupling has three main components: shafts, sleeve and key.

Figure 16.1                Muff Coupling

16.3.2    Design

16.3.2.1                      Design of Shafts

Shafts are designed on the basis of torsional shear stress induced because of the torque to be transmitted. Shear stress induced in shaft for transmitting torque, T is given by,

Where  T          = Twisting moment (or torque) acting upon the shaft,

J          = Polar moment of inertia of the shaft about the axis of rotation

 r           = Distance from neutral axis to the outer most fibre = d/2

So dimensions of the shaft can be determined from above relation for a known value of allowable shear stress, [τ].

16.3.2.2                      Sleeve Design

As discussed earlier, following relations are used to calculate the dimensions.

       D = 2d + 13                L = 3.5d      

Then the torsional shear stress in the sleeve is checked considering it as a hollow shaft.

Shear stress,

where, T          = Twisting moment (or torque) to be transmitted

J          = Polar moment of inertia about the axis of rotation

  r           = Distance from neutral axis to the outer most fibre = D/2

16.3.2.3                      Design of Key

Cross-section of the key is taken from the table corresponding to the shaft diameter or relations  (square key) or  and  (for rectangular key) are used to find the cross-section, where w is width and h is the height of the key.

Length of key in each shaft, .

The keys are then checked in shear and crushing.

Shear stress,
Crushing stress,

 

16.4          Clamp Coupling

16.4.1    Introduction

Clamp coupling is also known as split-muff coupling or compression coupling. In this coupling, sleeve or muff is made in two halves, which are split along the plane passing through the axes of the shafts. These two halves are clamped together with the help of bolts, which are placed in recesses made in the sleeve halves. Dynamic balancing of clamp coupling is difficult making it unsuitable for high speed applications. It is also unsuitable for shock loads. Assembly and dismantling is easier for this coupling. Figure 16.2 shows Clamp Coupling assembly.

A small clearance is provided between the two halves of the sleeve along the parting line and the force due to clamping of bolts creates frictional force between the surface of the shafts and inner surface of sleeve halves. Torque is transmitted by means of this frictional force and through the key, from the input shaft to the sleeve and from sleeve to the output shaft. It is not possible to find out the exact percentage of torque transmitted by friction and by the key. Therefore, for designing the bolts it is assumed that whole of the torque is transmitted by friction and while designing the key, it is assumed that whole of the torque is transmitted by it.

Design is similar to the design of muff coupling and an additional calculation is required for designing the bolts.

Figure 16.2                Clamp Coupling

 

16.4.2    Design

Design of Clamp Coupling is similar to the design of muff coupling and an additional calculation is required for designing the bolts.

16.4.2.1                      Design of Shafts

Same as discussed in sleeve coupling.

16.4.2.2                      Sleeve Design

Same as discussed in Sleeve Coupling

16.4.2.3                      Design of Key

Same as discussed in Sleeve Coupling

16.4.2.4                      Design of Bolts

Bolts are designed assuming that whole of the torque is transmitted by friction between sleeve and shafts.

Let       [σ_t]      = permissible tensile stress of bolts

              d_c       = core diameter of bolts

   n       = number of bolts

Clamping force of each bolt,

Figure 16.3          Forces acting on Bolts

Assuming that half of the bolts apply clamping force on one shaft and half of the bolts on the other. Clamping force on each shaft,

Frictional Torque,

where, m = coefficient of friction between shafts and sleeve.

Above two relations can be used to find the core diameter of the bolts by equating  to the total torque transmitted.

16.5          Flange Coupling

16.5.1    Introduction

Flange coupling consists of two flanges keyed to the shafts. The flanges are connected together by means of bolts arranged on a circle concentric to shaft. Power is transmitted from driving shaft to flange on driving shaft through key, from flange on driving shaft to the flange on driven shaft through bolts and then to the driven shaft through key again. Projection is provided on one of the flanges and a corresponding recess is provided in the other for proper alignment. Flange coupling is of two types – unprotected and protected. These are shown in Figure 16.3. If in case failure of bolts occurs during the operation, the bolts may hit the operator in case of unprotected flange coupling. To avoid this, protective circumferential flanges are provided in the protected type flange coupling.

Flange of a protected type flange coupling has three distinct regions – inner hub, flanges and protective circumferential flanges. Following standard proportions are used in the design of flange coupling:

Outer diameter of hub,                                               D = 2 d

Pitch circle diameter of bolts,                                     D₁ = 3 d

Outer diameter of flange,                                           D₂ = 4 d

Length of the hub,                                                      L = 1.5 d

Thickness of flange,                                                    t_f = 0.5 d

Thickness of protective circumferential flange,          t_p = 0.25 d

where d is the diameter of shafts to be coupled.

Figure 16.4                Flange Coupling

16.5.2    Design

16.5.2.1                      Design of Shafts

Same as discussed in sleeve coupling.

16.5.2.2                      Design of Hub

Hub is designed considering it as a hollow shaft, with inner diameter equal to diameter of shafts and outer diameter double of that. It is checked for torsional shear stress.

Shear stress,

Where  T = Twisting moment (or torque) to be transmitted

J = Polar moment of inertia about the axis of rotation

      r = Distance from neutral axis to the outer most fibre = D/2

16.5.2.3                      Design of Key

In this case two separate keys are used for the two shafts. Key is designed as discussed earlier. In this case, length of key,  (length of the hub)

16.5.2.4                      Design of Flange

The flange is subjected to shear at the junction of the hub as it transmits torque through the bolts. Area resisting shear  

where,  is the thickness of the flange.

If T is the torque to be transmitted, tangential force,
Shear stress,

 16.5.2.5                      Design of Bolts

Due to transmission of torque, force acts perpendicular to the bolt axes and the bolts are subjected to shear and crushing stresses. Let n be the total number of bolts.

Force acting on each bolt,

where D₁ is the pitch circle diameter of bolts.

Area resisting shear
where, dc = core diameter of bolts
Shear stress,
Area under crushing
Crushing stress,

 

References:

1. Design of Machine Elements by VB Bhandari
2. Analysis and Design of Machine Elements by VK Jadon
3. A Text Book of Machine Design by RS Khurmi