Tractor Systems and Controls 3(2+1)

Lesson 24. Analysis of steering-Turning radius. Ackerman Steering

The steering proposed by Erasmus Darwin in 1758 was patented by Rudolf Ackerman in 1817 is called Ackerman steering and is described below.

Fig. 24.1 shows the various linkages for going in a straight ahead situation. Fig 24.1 also shows the position of linkage for turning towards the right (lock position). For perfect steering in the locked position, the axes of all the wheels should appear to be meeting at one point, which is called the instantaneous turning centre.

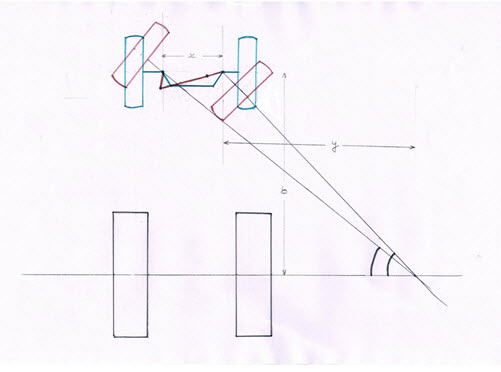
From Fig 24.1,

Tan \[\phi \] = wheelbase, b              - (1)

                        x+y

Tan θ = wheelbase, b              - (2)

                     y

θ - angle of inside lock

f - angle of outside lock

Subtracting (2) from (1)

Cot \[\phi \]  - cot θ = x/b                  - (3)

Ackerman steering

 

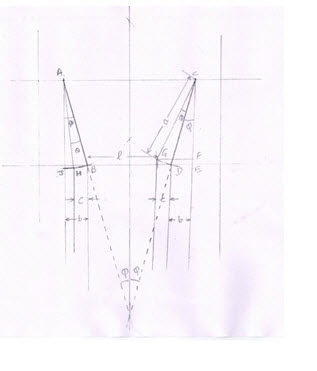
The Fig 24.2 has been derived from Fig 24.1.

AB and CD are the steering links from the two stub axles, each having a length of ‘a’.

BD is the tie rod of length ‘l’ between the two steering links.

The steering links AB and CD make an angle ‘φ‘ each with the lateral line about which the steering is symmetrical.

Now when the steering is turned to the right extreme, lock position, the steering link CD turns left by an angle ‘\[\phi \] and the link AB correspondingly turns left by an angle ‘θ’.

From the Fig 24.2,

In triangle CDE

Sin φ = b/a                  - (4)

In triangle CFG

Sin (φ+\[\phi \]) = (b+c)/a     - (5)

In triangle AHJ

Sin (φ-θ) = (b-c)/a      - (6)

Adding (5) and (6)

Sin (φ+\[\phi \]) + Sin (φ-θ) = (b+c)/a + (b-c)/a

                                         = 2 (b/a) = 2 (Sin φ)    - (7)

This relation for Ackerman steering holds for three cases i.e. when moving straight ahead, lock position to the right and lock position to the left.