Engineering Physics 3(2+1)

LESSON 8. Mathematical Derivation for Uncertainty Priciple

(1) Determining of the position of a particle by microscope

For the measured of position of a particle (electron) in the range of microscope the resolving power of the microscope can be measure the smallest distance between the two points,

Δ\[x={\lambda\over{2\sin \theta }}\]……..(1)

Δx - Uncertainty in determining the position of particle

\[\lambda\] - Wavelength of light used

\[\theta\] - Semi vertical angle of the cone of light

 To observed the particle (position of electron), it is necessary a photon strikes the electron (particle) and scattered inside the microscope.

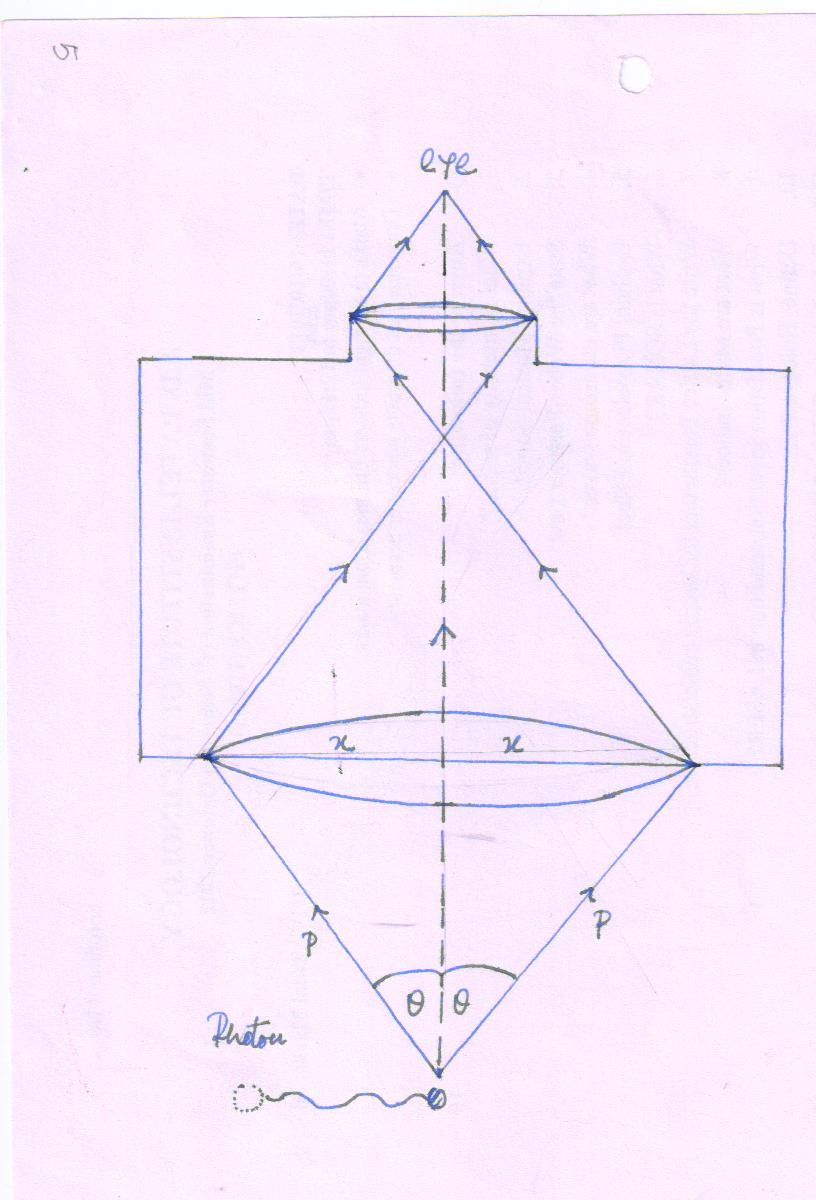
When a photon of initial momentum ρ = \[{h \over \lambda }\] after scattering (as a momentum is conserved in the collision) a particle enters in the field of view of microscope. A particle may be anywhere within angle 2\[\theta\]

Therefore, the momentum(x-component) in microscopic region is p sin \[\theta\] and -p sin \[\theta\]

Hence,

Δp = p sin \[\theta\] - (-p sin \[\theta\] )

Δp = 2p sin \[\theta\] 

But , p =   \[{h \over \lambda }\]

Δp  = \[{{2h\sin\theta}\over\lambda}\]……..(2)

From (1) and (2)

 Δx Δp = h

Product of uncertainties in position and momentum is of order of Plank’s Constant.

(2) Diffraction by single slit

Suppose a narrow beam of electrons passes through a single narrow slit (Δy) and produces a diffraction pattern on the screen.

Hence diffraction equation

\[d\sin \theta=n\lambda\]
For 1^st order

\[d\sin\theta=\lambda\]
d - Width of the slit = Δy

Δy sin  \[\theta\] =\[\lambda\]

Regarding diffraction pattern of on screen, all electrons have passed through the slit. But we can’t say that exact position of a particle within slit

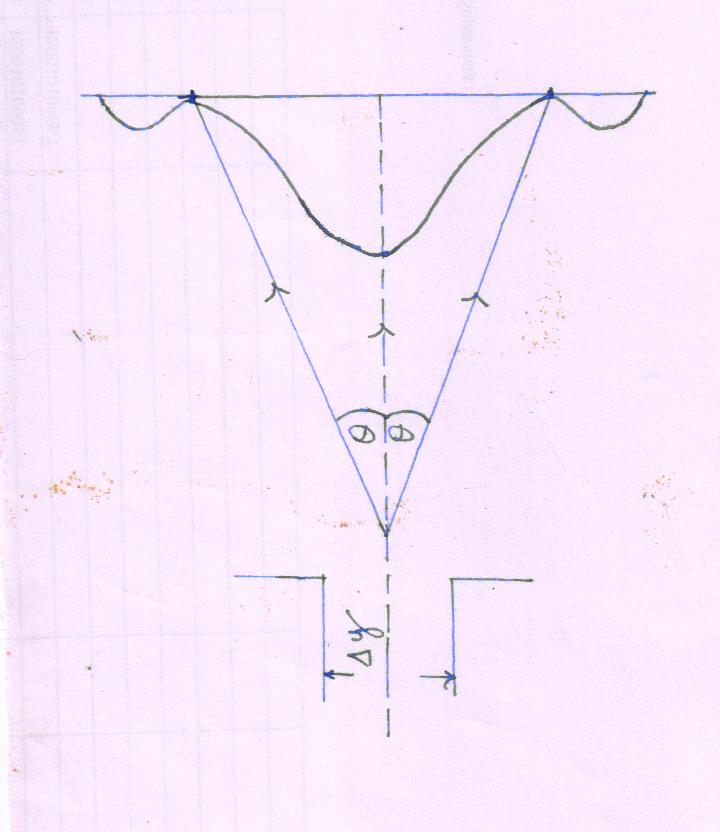
Hence the uncertainty can be determine the position of the electron equal to the width  Δy.

Δy =\[{\lambda \over{\sin \theta }}\]

Here, initially electrons are moving along -axis and they have no component of momentum along -axis. After diffraction at the slit electrons are deviated from their initial path to form diffraction pattern and have a component . The  y - component of momentum may lie between p sin \[\theta\]  and -p sin\[\theta\].

The uncertainties in y – component of momentum = Δp = 2p sin\[\theta\]

But, p  =  \[{h \over \lambda }\]

Δp = 2p sin\[\theta\] = \[{{2h\sin\theta}\over\lambda }\]

Δy Δp = \[{\lambda\over{\sin \theta }}\]  X \[{{2h\sin\theta }\over\lambda }\]

Δy Δp = 2h
 

Or

 Δy Δp  h

It shows the product of uncertainties in position and momentum is of order of Plank’s constant.