Engineering Physics 3(2+1)

LESSON 23. Application of Superconductor

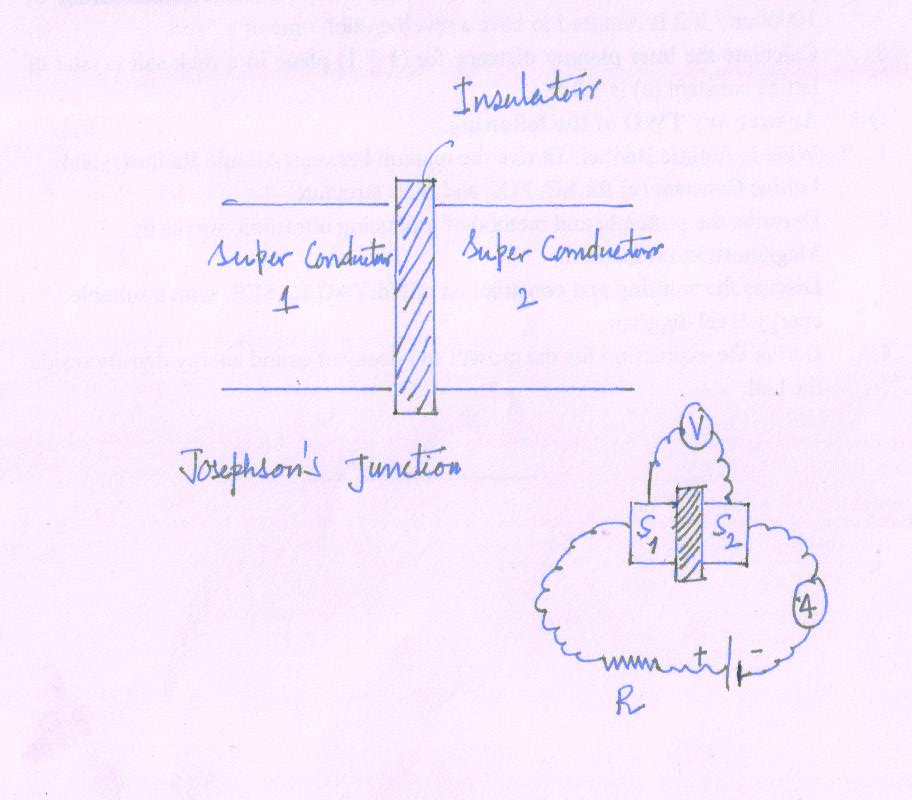
                                                     Fig.14(1)

 

DC Josephson Effect

• Two super conductors separated by thick insulator layer, say 10  thick, and are essentially two independe        nt superconductors without any joint properties.

• When insulator layer is thin, say 1 nm  thick, they become a system of coupled conductors. The cooper pairs tunnel through the barrier (insulating layer) as a single unit.

• The cooper pairs in a superconductor can be represented by a wave function, which is same for all pairs.

• The cooper pairs tunnel from one side of the junction to other side easily.

• The effect of the insulating layer is that it introduces a phase difference between the wave function of the pair on the other side. Because of this, supper current appears across the junction even through the applied voltage is zero. This is called dc Josephson Effect.

 It is noticed by

\[{I_s} = {I_c}\sin {\varphi _0}\]

\[{\varphi _0}\] is the phase difference between the wave function describing cooper pairs on the both side. 

\[{I_c}\] is critical current at zero voltage; depending upon the thickness, width of the insulator and temperature.

AC Josephson Effect

Suppose a dc voltage is applied across the junction, it introduces a addition phase on cooper pairs during tunneling.

So, a strictly new phenomenon will be observed.

The dc voltage generates an alternating current

\[I\] = \[{I_c}\sin \left( {{\varphi _0} + \Delta \varphi } \right)\]

Because of the dc voltage, the energy of the cooper pairs on both sides of the barrier differ by 2eV .

Using quantum mechanical calculation;

\[\Delta \varphi\]  = \[2\pi t\frac{{2eV}}{h}\]

\[I\] = \[{I_c}\sin \left( {{\varphi _0} + 2\pi t\frac{{2eV}}{h}{\text{}}} \right)\]

It is representing an alternating current which has frequency, ν = \[\frac{{2eV}}{h}\]

Thus, a dc voltage is applied across the junction; an ac current is produced.

SQUID

A superconducting quantum interference device (SQUID) is a device used to measure extremely weak magnetic flux.

• It is basically a sensitive magnetometer, which can measure very weak magnetic fields of the order of \[{10^{ - 13}}\frac{{Wb}}{{{m^2}}}\]

• The sensitivity of a SQUID to magnetic fields can be increased by using a flux transformer.

• The heart of a SQUID is a superconducting ring, which contains one or more Josephson Junctions.

There are main two types of SQUID;

(i)DC SQUID:

• It is made of two Josephson Junctions in parallel and relies on the interference of the current from each.
• It is more difficult and expensive to produce, but it is more sensitive.  

(ii) AC or RF SQUID:

• It is made of one Josephson junction.

Fabrication

• SQUIDs are usually fabricated from Lead or pure Niobium.

• The Lead is taken in the form of allow with 10% Gold or Indium.

• A thin Niobium layer deposited on to it acts as the base electrode of the SQUID and tunnel barrier is oxidized onto this Niobium surface.

• The schematic of a two-junctions SQUID (DC) is shown in Fig.14(2) and Fig.14(3) 

  

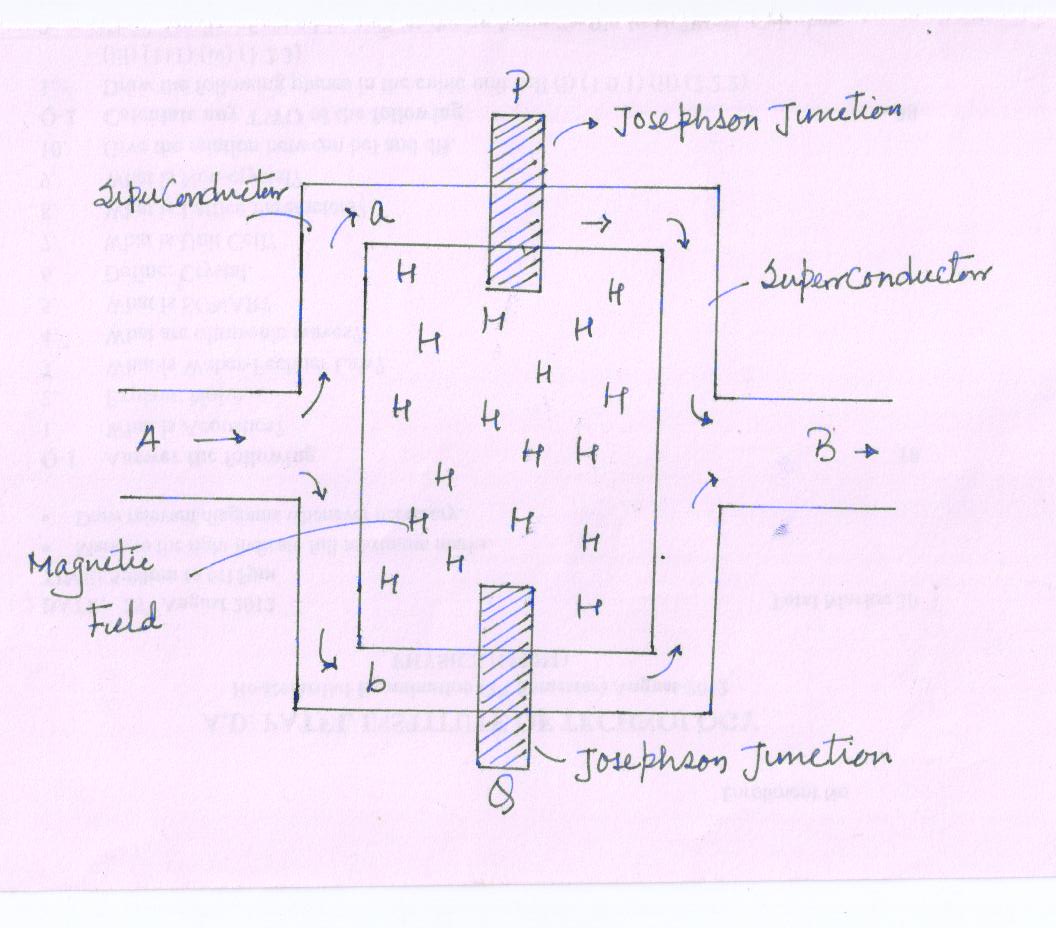
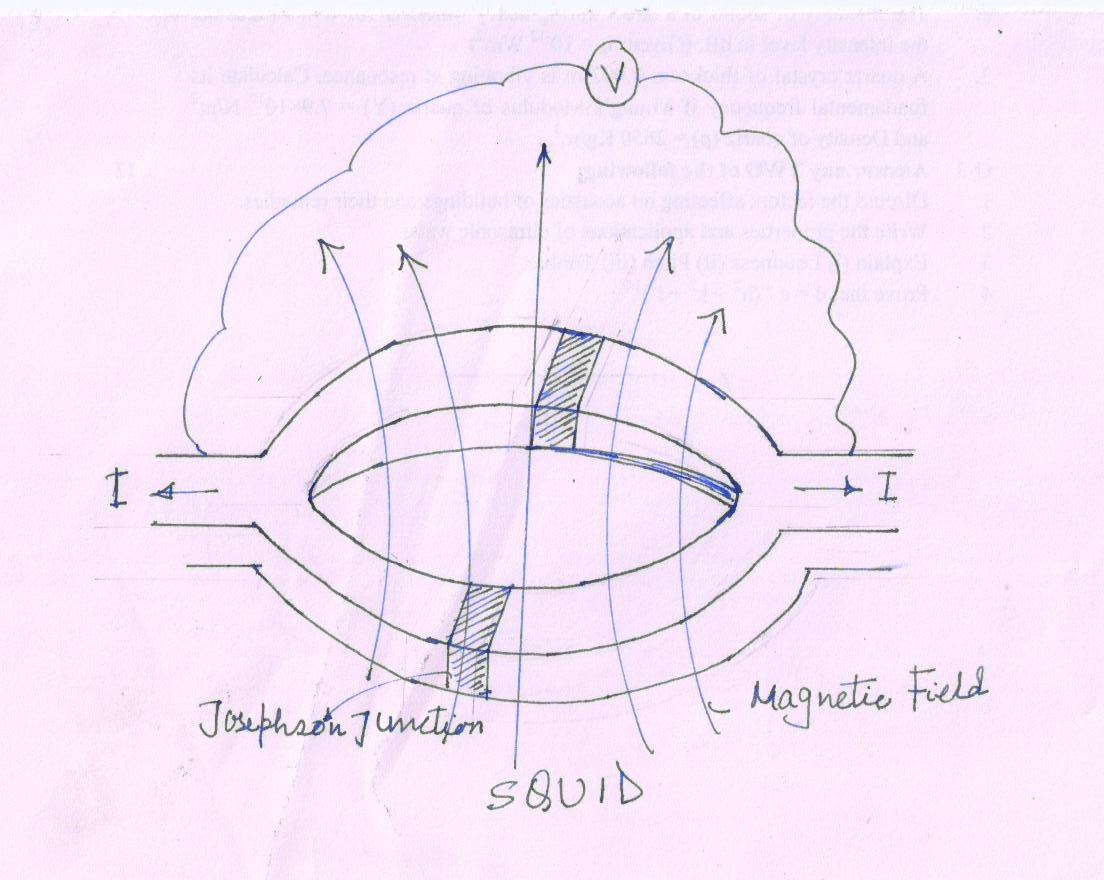
                             Fig.14(2)                                                         Fig.14(3)
  

  It consists of two Joseph junctions arranged in parallel so that electrons tunneling through the junctions demonstrate quantum interference.

•  The DC superconducting is applied to the SQUID. This current, called as bias current, enters into device through arm A.

• It is divided into two paths “a” and “b” and again recombines into one path. It leaves through the arm B.

• Here, P and Q are two Josephson junctions with different thickness of the insulators P and Q. The \[{I_1}\] and  \[{I_2}\] are tunneling current through junctions P and Q respectively.

• In superconductor, the wave function experiences a phase shift at the junction P and Q. 

• Suppose phase difference between points A and B taken on the path through junction P be \[{\delta _a}\] and the phase difference between points A and B taken on the path through junction Q be \[{\delta _b}\]  .

• Hence, in absence of magnetic field these two phases are equal i.e phase difference is zero. \[{\delta _b}\] - \[{\delta _a}\] = 0

• Now, the magnetic field is applied perpendicular to the loop,

The flux passes through the loop, and changes the quantum mechanical phase difference across each of the two junctions. The wave functions at the two Josephson junctions interfere with each other. The super current flows along the paths a and b interfere. Hence, the device is called SQUID.

In super conductor, the waves are de Broglie wave of cooper pair and phase difference is caused by the applied magnetic field. So, according the Josephson’s theory the phase difference between re collected current is directly proportional to the magnetic flux ( \[{\Phi _0}\] )  through ring

Total current \[{I_L}\] = 2 \[({I_0}\sin {\delta _0})\cos \frac{{\Phi }}{{\hbar c}}\] 

It indicates a progressive increase or decrease of the magnetic flux causes the current to oscillate between a maximum and a minimum value. Maxima in the current occur whenever the magnetic flux increases by one flux.

In practice, instead of the current, we measure the voltage across the SQUID which also oscillates with the changing magnetic field. Thus, the SQUID is a flux to voltage transducer which is converting a tiny change in magnetic flux into voltage. The flux ( \[\phi\] ) is related to the magnetic field B. Hence, \[\phi\] =  BA

 is Area of the ring.

Application of SQUID

• SQUIDs are use to measure very small magnetic field ( \[{10^{ - 13}}\frac{{Wb}}{{{m^2}}}\] ). Hence it acts as a very sensitive magnetometer.

• In geology, it is used to measure rock magnetism and conditional drift.

• It is also used in non-destructive test, testing of corrosion of aluminum sheet riveted together in aircraft.

• The extreme sensitivity of SQUIDs makes them ideal for studies in biology. Magnetoencephalography (MEG), for example, uses measurements from an array of SQUIDs to make inferences about neural activity inside brains

• In the clinical environment SQUIDs are used in cardiology for magnetic field imaging (MFI), which detects the magnetic field of the heart for diagnosis and risk stratification

• Probably the most common commercial use of SQUIDs is in magnetic property measurement systems (MPMS)

• SQUIDs are being used as detectors to perform magnetic resonance imaging (MRI).

• A potential military application exists for use in anti-submarine warfare as a magnetic anomaly detector (MAD) fitted to maritime patrol aircraft.