Engineering Physics 3(2+1)

LESSON 32. Law of Photometry

The intensity of illumination of surface E = \[{{Theamountoflightwhichflowfromilluminatingsurfacepersec} \over {Areaofilluminatiom}}\]

For surface A, E₁ = \[{Q \over A}\] = \[{Q \over {4\pi r_1^2}}\]

A Surface area of the circle

 For surface B, E₂ = \[{Q \over {4\pi r_2^2}}\] ……… (1)

But illumination power (I) = \[{{LuminousFlux} \over {SolodAngle}}\]

I  = \[{Q \over {4\pi }}\] …… (2)

From equation (1) and (2)

Lambert’s Cosine Law

“The illumination is directly proportional to the “Cosine of the angle made by the normal to the illuminating surface with the direction of the incident flux”. 

• Note: Cosine angle either angle between the normal and the direction of the incident flux or the angle between two plane surfaces (one is normal incident surface and other is bend surface)

Lambert derived a relation between normal illumination E_n  and slanting illumination E for the same distance.

Let S is point source at distance r from surface area ds (original)

I is luminous intensity or illumination power of the point source(S)

dω is solid angle; subtended by ds and slanting area are same at point source(S)

θ is the angle between normal to the surface area ds and the direction of incident flux.

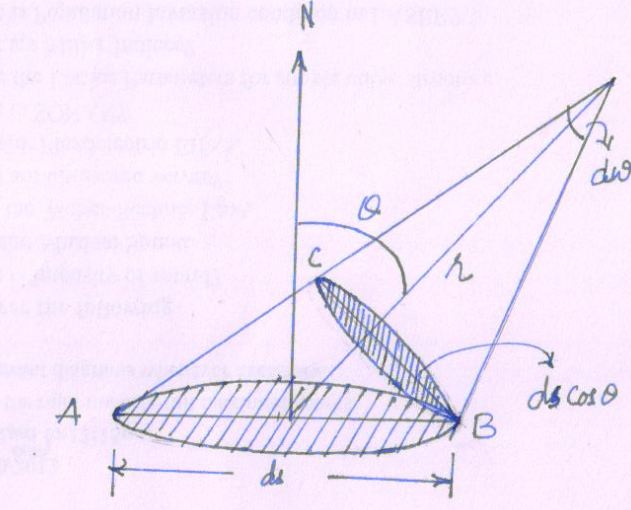
Fig 21(2)

According to resolved figure,

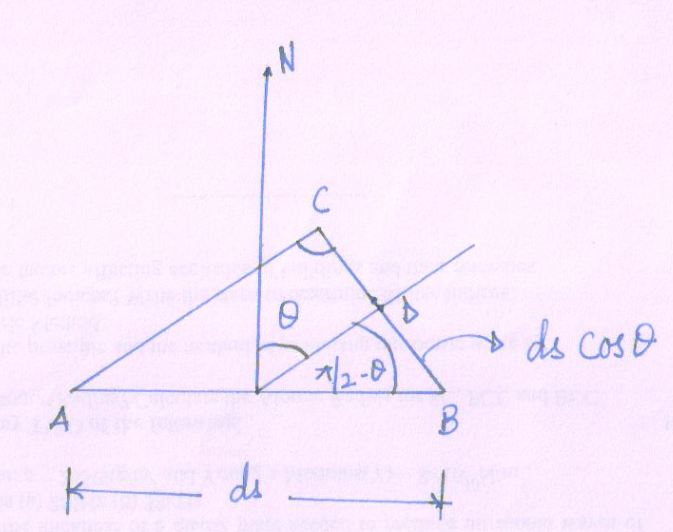
Fig 21(3)

\[ds\cos \theta\]  = \[x\] = BD

Luminous Intensity (I) =  \[{F \over w}\]

But dF are fluxes in solid angle  dω

I =  \[{dF \over dw}\]

Solid angle dω =  ^{\[{{ds\cos \theta } \over {{r^2}}}\]}

dF  =   I dω

dF   =  \[{{Ids\cos \theta } \over {{r^2}}}\]

I = \[{{{r^2}dF} \over {ds\cos \theta }}\]

Expression reports

Light illumination with intensity I and making solid angle \[{{ds\cos \theta } \over {{r^2}}}\] w.r.t area ds cos \[\theta\] . Due to that solid angle, luminous flux dF is slanting with angle \[\theta\]  and focusing to surface ds (original).

Light illuminates with intensity I from source. Source is slanting mode w.r.t. normal. It is going to illuminates original surface ds. So, intensity fluxes dF illuminating the surface with slanting angle cos \[\theta\] and with dF flux is illuminating surface ds.

Illumination or Intensity of illumination of surface E  =   \[{F \over A}\]

Hence E = \[{dF \over dS}\]

E =  \[{{Ids{\rm{Cos\theta }}} \over {ds{r^2}}}\]

E =  \[{{I{\rm{Cos\theta }}} \over {r^2}}\] …… (2)

For Normal (direct) illumination

En =  \[{I \over {{r^2}}}\]

 E = En Cos \[\theta\]…… (3)

Equations (2) and (3) are the two form of Lambert’s Law