Micro Irrigation Systems Design 3(2+1)

Lesson 15. Hydraulic Design of Sprinkler Systems

15.2 Computation of Pressure Variation in Pipes

The performance of sprinklers system is related to operating pressure in the pipe line, the frictional loss in pipe and fitting, and differentials elevations caused pressures to vary in a field. Frictional loss causes the pressure to decreases in the downstream direction, while chances in evaluations can cause either an increase or decrease in pressure (depending on where the evaluation is downhill or uphill).  The difference in pressure between upstream and downstream of a pipe line can be estimated by

                                             

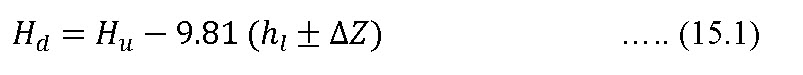
where

           = pressure at down and upstream positions, respectively ( kPa). 

 = this is energy loss in pipe between up and downstream positions (m).

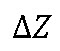          = difference in elevation between up and downstream positions (m).

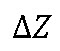 is (+) when change in elevation between the up- and downstream positions is uphill. This sign is (-) when the elevation at the upstream location exceeds the elevation at the downstream location.

                                                        

 = constant that depends on number of outlets(sprinkler or laterals) removing water from the pipe between the up- and downstream location. The value of F can be selected from Table 15.1. F also depends on the method used estimate head loss due to friction ( ).

The value of F can be computed from Equation 15.3 when distance to the first sprinkler equals the sprinkler head spacing.

                   F = 

The values of F can be estimated from Equation 15.4 when the distance to the first sprinkler equals one-half of the sprinkler head spacing.

F =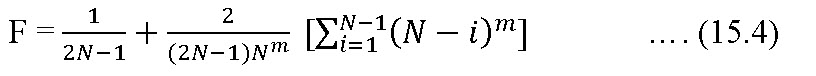   

m = a constant depends on a particular equation to be used to compute

        N = no. of sprinklers or outlets.

 =friction loss in pipe between up and downstream locations(m)

minor loss through fittings (m)

Minor losses caused by sprinkler risers and other fittings are usually small and these are neglected.  

Head loss due to friction ( in pipe line can be computed using following equation

                                             

where

K = friction factor that depends on pipe material

L = length of pipe (m)

Q = flow rate (L min^-1)

D = diameter of pipe (m)

c, m, n are constants to be used from following Table 15.2

 Table 15.1. Correction factor ‘F’ for friction losses in aluminum pipes with multiple outlets

No. of sprin- klers on lateral	1st sprinkler is one sprinkler interval from main	1st sprinkler is 1/2 sprinkler interval from main	No. of sprinklers on lateral	1st  sprinkler is one sprinkler interval from main	1st sprinkler is1/2 sprinkler interval from main
1	1.000	1.000	16	0.365	0.345
2	0.625	0.500	17	0363	0.344
3	0.518	0.422	18	0.361	0.343
4	0.469	0393	19	0.360	0.343
5	0.440	0.378	20	0.359	0.342
6	0.421	0.369	22	0.357	0.341
7	0.408	0.363	24	0.355	0.341
8	0398	0.358	26	0.353	0.340
9	0.391	0.355	28	0.351	0.340
10	0.385	0.353	30	0.350	0.339
11	0.380	0.351	35	0.347	0.338
12	0.376	0.349	40	0.345	0.338
13	0.373	0.348	50	0.343	0.337
14	0.370	0.347	100	0.338	0.337
15	0.367	0.346	>100	0.335	0.335

   (Source:  Michael A.M (2010)

  Table 15.2 Constants needed to use Equation 15.5

Method of Computing,	c (SI Units)	m	n
Darcy –Weisbach	277778	2.0	1.0
Hazen- Williams	591722	1.85	1.17
Scobey	610042	1.90	1.10

 

For the Darcy- Weisbach equation, K in Eq. 15.5 is given by

K = 0.811 (       )

 where

f = friction factor to be obtained from Moody diagram

g = acceleration due to gravity (9.81 m s^-2)

For Hazen- Williams Equation, K in Eq. 15.5 is given by

                                         

The value of C depends on type of pipe material. It ranges from 100 (Brick sewer) to 150(Cement lined). For Plastic pipe, C is 140-150.

For Scobey Equation, K in Eq. 15.5 is given by

                                                                

The values of  depends on types of pipe material its fittings and diameter. It ranges from 0.33 (75 mm diameter Welded steel pipe) to 0.43 (Aluminum pipe with coupler each of 6 m long).

Table 15.3 is ready reckoner table for estimation of head loss due to friction from Aluminum pipe or choosing size of pipe for a given discharge and friction loss.

 Table 15.3 Friction loss in meters per 100 meters in lateral line of portable aluminum pipe with coupling (Based on Scobey’s formula and 9 meters pipe length) 

Flow litres/sec	Diameter of pipe
	5.0 cm Ks 0.34	7.5 cm Ks 0.33	10.0 cm Ks 0.32	12.5 cm Ks 0.32	15.0 cm Ks 0.32
1.26	0.32
1.89	2.53
2.52	4.49	0.565	0.130
3.15	6.85	0.858	0.198
3.79	9.67	1.21	0.280
4.42	12.9	1.63	0.376	0.122
5.05	16.7	2.10	0.484	0.157
5.68	20.8	2.63	0.605	0.196
6.31	25.4	3.20	0.738	0.240	0.099
7.57		4.54	1.04	0.339	0.140
8.83		6.09	1.40	0.454	0.188
10.10		7.85	1.80	0.590	0.242
11.36		9.82	2.26	0.733	0.302
12.62		12.0	2.76	0.896	0.370
13.88		14.4	3.30	1.07	0.443
15.14		16.9	3.90	1.26	0.522
16.41		19.7	4.54	1.47	0.608
17.67		22.8	5.22	1.70	0.700
18.93		25.9	5.96	1.93	0.798
20.19		29.3	6.74	2.18	0.904
21.45		32.8	7.56	2.45	1.02
22.72		36.6	8.40	2.74	1.13
23.98		40.6	9.36	3.03	1.26
25.24		44.7	10.3	3.34	1.38
26.50			11.3	3.66	1.51
27.76			12.3	4.00	1.66
29.03			13.4	4.35	1.80
30.29			14.6	4.72	1.95
31.55			15.8	5.10	2.12
34.70			18.9	6.12	2.52
37.86			22.2	7.22	2.98
41.01			25.9	8.40	3.46
44.17			29.8	9.68	3.99
47.32			33.8	11.0	4.54
50.48				12.5	5.15
53.63				14.0	5.78
56.79				15.6	6.44
59.94				17.3	7.14
63.10				19.0	7.86

(Source:  Michael A.M (2010)

 15.3 Design of Sprinkler Laterals

The sprinklers are attached on laterals at equal spacing. The flow through lateral pipe is spatially varied with decreasing discharge. In spatially varied with decreasing discharge. In the beginning, the flow will equal the combined discharge of all the sprinklers. This will decrease along the line until, at the farthest end, there will be only the flow of the last sprinkler. Therefore the friction loss in a lateral will be much less than if the total flows were carried through the entire length of the line. It is recommended that the total pressure variation is the laterals should not exceed more than 20% of the higher pressure.

Where, the friction loss, H_f in the laterals is within 20% of the average pressure.

 The average head (H_a) in a sprinkler line can be expressed approximately by

             

In which  = pressure at the sprinkler at the sprinkler on the farthest end (Fig. 15.1).

 = head loss due to friction

If the lateral is on nearly level land or on the contour, the pressure head ()  at the main is given by

                                                   

 By solving for H_o, in (15.9) by substituting in Equation (15.10), and by making an allowance for differences in elevation along the lateral

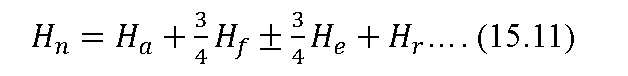
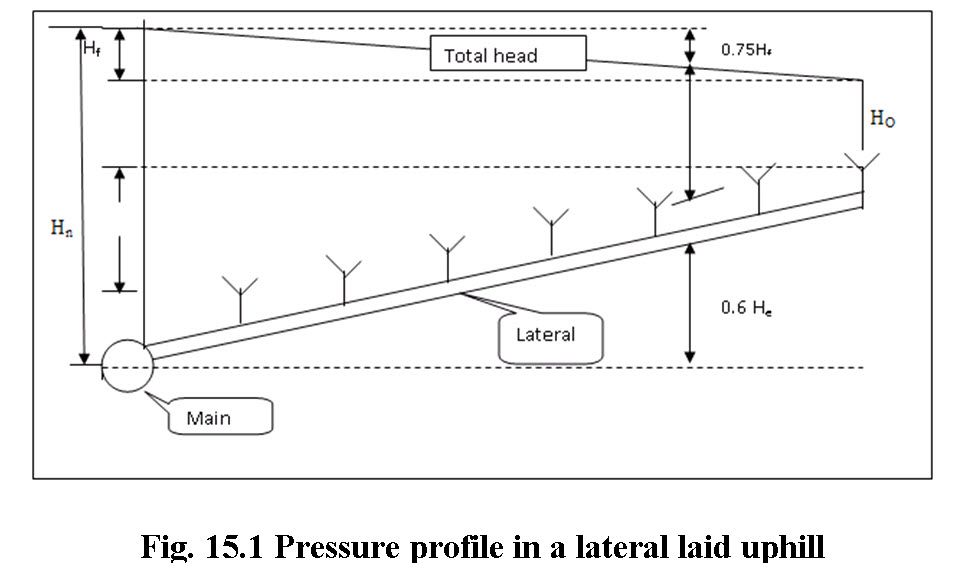
in which,

H_e = maximum difference in elevation between the first and last sprinkler, m

 = the riser height, m

The term 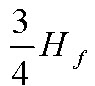 is positive if lateral runs up the slope and negative, if lateral runs down the slope. The term is an approximation since allowance for the difference in elevation varies with number of sprinklers on the laterals.

Allowance due to lateral running on uphill and downhill conditions should be made while determining the head variation. The design capacity for sprinklers on lateral is based on the average operating pressure.

 Size of Main Line Pipe

The size of main line is selected such that the annual water application cost is as low as possible. Normally friction loss of 3m for small system and 12m for large systems is allowed.

15.4 Pumps and power units

In selecting a suitable pump, it is necessary to determine the maximum total head against which the pump is working. This may be determined by

                  

in which,

H_t= total design head against which the pump is working, m
H_n = maximum head required at the main to operate the sprinklers on the lateral at the required average pressure, including the riser height, m

H_m = maximum friction loss in the main and in the suction line, m

H_J = elevation difference between the pump and the junction of the lateral and the main, m, and

H_s= elevation difference between the pump and the source of water after drawdown, m

The amount of water that will be required is determined by multiplying the number of sprinklers by the capacity of each. When the rates of pumping are known, the pump may be selected from rating curves or tables provided by manufactures.

The horse power requirement of pump can be estimated by

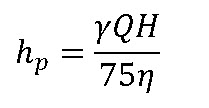
where,

          = unit of water

          Q= pump discharge

          H= Total head (m)

          = efficiency of pump

 Example: 37.1

Design a sprinkler irrigation system to irrigate 5 ha Wheat crop.

Assume

Soil type                                       = silt loam

Infiltration rate at field capacity    = 1.25 cm/h

Water holding capacity                  = 15 cm/m

Root zone depth                             = 1.5 m

Daily consumptive use rate           = 6 mm d^-1

Sprinkler type                                = Rotating head

 Solution:

Step I

Maximum water application rate = 1.25 cm/h

 Step II

Total water holding capacity of the soil =15 x 1.5 = 22.5 cm

Let the water be applied at 50% depletion, hence the depth of water to be applied

= 0.50 x 22.5 = 11.25cm

Let the water application efficiency be 90 per cent

Depth of water to be supplied = 11.25 / 0.9 = 12.5 cm

Step III

For daily consumptive use rate of 0.60 cm;

Irrigation interval = 11.25 / 0.6 = 19 days

In period of 19 days, 12.5 cm of water is to be applied on an area of 5 ha. Hence assuming 10 hrs. of pumping per day, the sprinkler system capacity would be

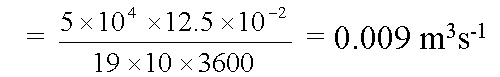=  = 0.009 m³s^-1

 

Step IV

Spacing of lateral (Sm) = 18 m

Spacing of Sprinklers in lateral (Si) = 12 m  

This selection is based on after the following consideration:

Operating pressure of nozzle         = 2.5 kg/cm²

Maximum application rate             = 1.25 cm/h

Referring sprinkler manufacturer’s M/S NOCIL, Akola chart (Table 15.4), the nozzle specifications with this operating pressure and application rate is:

Nozzle size                : 5.5563 x 3.175 mm

Operating pressure    : 2.47 kg/cm² and

Application rate         : 1.10 cm/hr (which is less than the maximum allowable   

                                     application rate)

Diameter of coverage  : 29.99 ≈ 30.0 m

Discharge of the nozzle : 0.637 L s^-1 = 0.637 x 10^-3 m³s^-1

 

Step V

Total no. of sprinkler required = 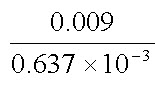= 14.12 ≈ 14 sprinklers

Therefore 7 nos. of sprinklers on each lateral.

Step VI

The sprinklers will be spaced at 12m intervals on each of two lateral lines spaced 18 m apart.

Step VII

Total length of each lateral = 12 x 7 = 84

Operating pressure = 2.47 kg/cm²

Total allowable pressure variation in the pressure head is 20%, hence maximum allowable pressure variation in pressure = 0.2 x 2.47 = 0.494 kg/cm² = 4.94 m

Variation of pressure due to elevation = 2 m

Permissible head loss due to friction   = 4.94 – 2 = 2.94 m

Total flow through the lateral = 7 x 0.637 x 10^-3 = 4.459 x 10^-3 m³s^-1

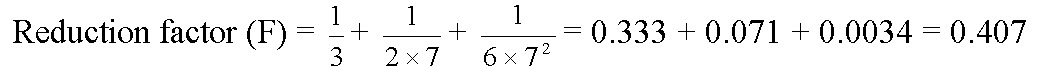
The head required to operate the lateral lines (H_m) = 24.7 + 2.94 + 2 + 1 = 30.6 m

Frictional head loss in main pipe line (H_f) = 30.6  0.2 = 6.12 m

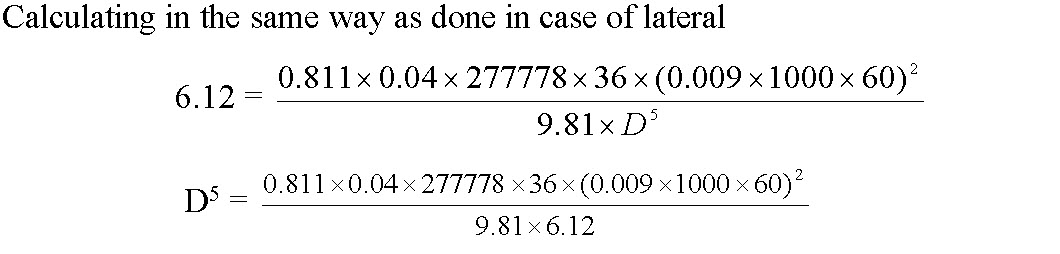
Or,     D = 69.10 ≈ 75 mm

Total design head (H) = H_m+ H_f +H_j +H_s

Where

H_j = Difference in highest junction point of the lateral and main from pump  

level = 0.5 m (assume)

H_s = Suction lift (20 m, assume)

H = 30.6 + 6.12 + 0.5 + 20 = 57.22 m

The pump has to deliver 0.009 m³s^-1 of water against a required head of 57.22 m

Hence, the horse power of a pump with 60% efficiency

  = 11.44 hp

(Source: Tiwari, 2009)

Table: 15.4 Design specifications of sprinkler with different nozzle size and operating pressure for high pressure models Model HP.

Nozzle Size		Operating Pressure		Dia of Spray		Discharge		Application rate
								12 x 12		12 x 18		18 x 18		18 x 24		24 x 24
Range	Spread	Kg/cm2	psi	m	ft	L s-1	gpm	cm/h	in/h	cm/h	in/h	cm/h	in/h	cm/h	in/h	cm/h	in/h
7/32” 5.5563mm	1/8” 3.175mm	2.11 2.47 2.82 3.17 3.52 4.23	30 35 40 45 50 60	27.7 29.9 32.0 33.9 35.8 39.2	92.3 99.7 106.7 113.0 119.3 130.7	0.588 0.637 0.680 0.721 0.760 0.833	7.76 8.40 8.97 9.51 10.03 10.99	1.50 1.60 1.70 1.80 1.90 2.10	0.58 0.63 0.67 0.71 0.75 0.82	NA 1.10 1.10 1.20 1.30 1.40	NA 0.42 0.45 0.47 0.50 0.53	NA 0.71 0.76 0.80 0.74 0.93	NA 0.28 0.30 0.32 0.33 0.36	NA NA NA NA 0.63 0.69	NA NA NA NA 0.25 0.27	NA NA NA NA NA 0.52	NA NA NA NA NA 0.20
9/32” 7.1438mm	1/8” 3.175mm	2.11 2.47 2.82 3.17 3.52 4.23	30 35 40 45 50 60	31.4 34.0 36.3 38.5 40.6 44.5	104.7 113.3 121.0 128.3 135.3 148.3	0.878 0.950 1.016 1.077 1.135 1.244	11.59 12.54 13.41 14.21 14.98 16.42	2.20 2.40 2.50 2.70 2.80 3.10	0.86 0.94 1.00 1.10 1.10 1.20	1.50 1.60 1.70 1.80 1.90 2.10	0.58 0.62 0.67 0.71 0.74 0.82	0.98 1.10 1.10 1.20 1.30 1.40	0.39 0.42 0.44 0.47 0.50 0.54	NA NA 0.85 0.90 0.95 1.00	NA NA 0.33 0.35 0.37 0.41	NA NA NA NA 0.71 0.78	NA NA NA NA 0.28 0.31
3/8” 9.525mm	1/8” 3.175mm	2.11 2.47 2.82 3.17 3.52 4.23	30 35 40 45 50 60	36.3 39.2 41.9 44.5 46.9 51.4	121.0 130.7 139.7 148.3 156.3 171.3	1.449 1.568 1.676 1.777 1.872 2.052	19.12 20.69 22.12 23.45 24.71 27.08	3.60 3.90 4.20 4.40 4.70 5.10	1.40 1.50 1.60 1.70 1.80 2.00	2.40 2.60 2.80 3.00 3.10 3.40	0.95 1.00 1.10 1.20 1.20 1.30	1.60 1.70 1.90 2.00 2.10 2.30	0.63 0.69 0.73 0.70 0.82 0.90	1.20 1.30 1.40 1.50 1.60 1.70	0.48 0.51 0.55 0.58 0.61 0.67	NA 0.98 1.00 1.10 1.20 1.30	NA 0.39 0.41 0.44 0.46 0.50

 Table:15.5 Design specifications of sprinkler with different nozzle size and operating pressure for low pressure models Model LP

Nozzle Size		Operating Pressure		Dia of Spray		Discharge		Application rate
								6 x 6		6 x 9		9 x 9		6 x 12		12 x 12
Range	Spread	Kg/cm2	psi	m	ft	L s-1	gpm	cm/h	in/h	cm/h	in/h	cm/h	in/h	cm/h	in/h	cm/h	in/h
7/32” 5.5563mm	1/8” 3.175mm	1.06 1.41 1.76 2.11 2.47 2.87	15 20 25 30 35 40	19.6 22.6 25.3 27.7 29.9 32.0	65.3 75.3 84.3 92.3 99.7 106.7	0.417 0.481 0.537 0.588 0.637 0.680	5.50 6.34 7.08 7076 8.40 8.97	4.20 4.80 NA NA NA NA	1.60 1.90 NA NA NA NA	2.80 3.20 3.60 3.90 4.20 4.50	1.10 1.30 1.40 1.50 1.70 1.80	1.90 2.10 2.40 2.60 2.80 3.00	0.73 0.84 0.94 1.00 1.10 1.20	2.10 2.40 2.70 2.90 3.20 3.40	0.82 0.95 1.10 1.20 1.30 1.30	1.00 1.20 1.30 1.50 1.60 1.70	0.41 0.47 0.53 0.58 0.63 0.67
13/64” 5.1594mm	1/8” 3.175mm	1.06 1.41 1.76 2.11 2.47 2.82	15 20 25 30 35 40	18.9 21.8 24.3 26.7 28.9 30.8	63.0 72.7 81.0 89.0 96.3 102.7	0.374 0.431 0.482 0.527 0.571 0.610	4.93 5.68 6.36 6.95 7.53 8.05	3.70 4.30 4.80 NA NA NA	1.50 1.70 1.90 NA NA NA	2.50 2.90 3.20 3.50 3.80 4.10	0.98 1.10 1.30 1.40 1.50 1.60	1.70 1.90 2.10 2.30 2.50 2.70	0.65 0.75 0.84 0.92 1.00 1.10	1.90 2.20 2.40 2.60 2.90 3.10	0.74 0.85 0.95 1.00 1.10 1.20	NA 1.11 1.20 1.30 1.40 1.50	NA 0.42 0.47 0.52 0.56 0.60
5/32” 3.9688mm	1/8” 3.175mm	1.06 1.41 1.76 2.11 2.47 2.82	15 20 25 30 35 40	16.5 19.1 21.3 23.4 25.3 27.0	55.0 63.7 71.0 78.0 84.3 90.0	0.263 0.303 0.339 0.371 0.401 0.429	3.47 4.00 4.47 4.89 5.29 5.66	2.60 3.00 3.40 3.70 4.00 4.30	1.00 1.20 1.30 1.50 1.60 1.70	1.80 2.00 2.30 2.50 2.70 2.90	0.69 0.80 0.89 0.97 1.10 1.10	1.20 1.30 1.50 1.60 1.80 1.90	0.46 0.53 0.59 0.65 0.70 0.75	1.30 1.50 1.70 1.90 2.00 2.20	0.52 0.60 0.67 0.73 0.79 0.84	NA NA 0.88 0.93 1.00 1.10	NA NA 0.35 0.37 0.39 0.42

 

References:

• Michael, A. M., (2010). Irrigation Theory and Practice, Vikas Publishing House PVT Ltd, Delhi, India, pp. 595,745.

• Tiwari. K. N. (2009) Pressurized Irrigation, Precession Farming Development Center Publication No. PFDC/ IIT KGP/2/2009:pp.53.

Suggested Reading:

• Wu, I. P., (1997). An Assessment of Hydraulic Design of Micro-Irrigation Systems. Agricultural Water Management. 32(3):275–284.

• Mofoke, A. L. E., Adewumi, J. K., O. J., Mudiare, and Ramalan, A. A.(2004) Design, Construction and Evaluation of an Affordable Continuous Flow Drip Irrigation System, Journal of Applied Irrigation Science. 39(2): 253-269.

• Savva, A. P., Frenken, K., (2002) Irrigation Manual; Planning, Development Monitoring and Evaluation of Irrigated Agriculture with Farmer Participation, FAO, SAFR, Harare.