Heat and Mass Transfer 2(2+0)

Lesson-32 Reynolds Analogy and Numerical problems

The governing equation for convective mass transfer is similar to the convective heat transfer equation and is expressed as

m_b =  h_mc ( C_b1 –C_b2)                                                                 (1)

where

           m_b is is the diffused mass of component ‘b’

           h_mc is mass transfer coefficient of component ‘b’

           C_b1 and C_b2 are mass concentrations of component ‘b’

For steady state, one dimensional diffusion of a fluid across layer of thickness (X₂ –X₁), mass diffusion can be expressed as

Comparing equations (11) and (12), we get

Equation (3) represents mass transfer coefficient based on concentration gradient.

We know that mass flux or flow per unit area is represented as

Using equation (3), equation (4) can be written as

Where h_mp is mass transfer coefficient based on pressure

h_mp = h_mc M_b / GT 

=  h_mc  / RT                  (6)

For diffusion of water vapor through a layer of stagnant air, mass diffusion for water is expressed as

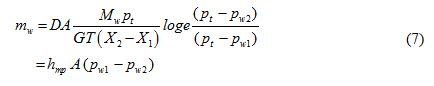
Mass transfer coefficient, h_mp, based on pressure difference can be written as

Mass transfer coefficient, h_mc, based on concentration gradient can be expressed as

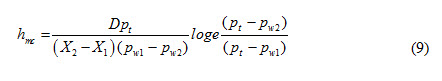
Reynolds Analogy:

The Reynolds analogy describes analogous behavior of mass, momentum and heat transfer and it was first recognized by Reynolds. The convective transport of mass, momentum and heat normally occur through a thin boundary layer close to the wall. The equations governing the transport of these quantities are analogous if the pressure gradient is equal to zero and the Prandtl Number (Pr) and Schmidt Number (Sc) are equal to unity. Under these conditions, their non-dimensional convective transport coefficients are related by the equation given below

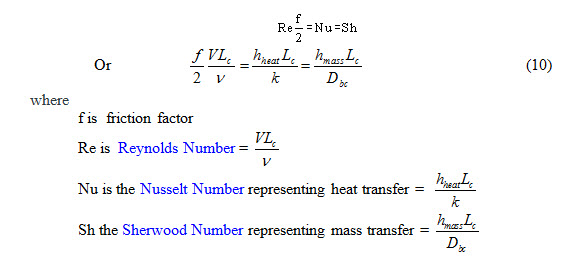
Equation (10) is known as the Reynolds analogy, and enables the calculation of heat transfer coefficient if either the friction factor or the mass transfer coefficient is known.

Example 14.1 Estimate the diffusion coefficient for ammonia in air at 25°C temperature and one atmospheric pressure.

For ammonia:

Molecular weight =20 and molecular volume = 25.81 cm³/gm mole

For air:

Molecular weight = 26and molecular volume = 29.89 V cm³/gm mole

Solution:      

Example 14.2 A rectangular system having steel walls of 8 mm thickness stores gaseous hydrogen at elevated pressure. The molar concentration of hydrogen in the steel at the steel at the inner and outer surfaces of the wall are approximated to be 1.0 kg-mol/m³ and 0.0 kg-mol/m³ respectively. Presuming that the binary diffusion coefficient for hydrogen in steel is 0.2410^-12 m²/s, workout the diffusion flux for hydrogen through the steel wall. Point out the assumptions made in the derivation of the relation used by you.

Solution:      

Example 14.3 A plastic membrane 0.25 mm thick has hydrogen gas maintained at pressures of 2.5 bar and 1 bar on its opposite sides. The binary diffusion coefficient of hydrogen in the plastic is 8.510^-8 m²/s and the solubility of hydrogen in the membrane is 1.510^-3kg-mol/ m²-bar. Under uniform temperature conditions of 25°C, workout: (a) molar concentrations of hydrogen at the opposite faces of the membrane, (b) molar and mass diffusion flux of hydrogen through the membrane.

Solution:     

Example14.4 Hydrogen gas at 1 bar and 400 k flows through a rubber tubing of 10mm inside radius and 20 mm outside radius. The diffusivity of hydrogen through rubber is stated to be 0.7510^-4 m²/hr and the solubility of hydrogen is 0.052 m³ of rubber t 1 atmosphere. What would be the diffusion loss of hydrogen per metre length of the rubber tubing? It may be presumed that resistance to diffusion of hydrogen from the outer surface of the tube is negligible.

Solution:   

Example14.5 The air pressure in a tyre tube of surface area 1 m² and wall thickness of 0.01m is approximated to drop from 2 bar in a period of 5-days. The solubility of air in rubber is 0.07m³ of rubber at 1 bar. Estimate the diffusivity of air in rubber at the operating temperature of 200 k if the volume of air in the tube is 0.025m³.

Solution:    

Example14.6 A distillation column containing a mixture of benzene and toluene is at a pressure of 1 atmosphere and 50°C temperature. The liquid and vapour phases contain 30 mol% and 45 mol % of benzene. At 50°C temperature, the vapour pressure of toluene is 70kN/m² and the diffusivity is 510^-6 m²/s. workout the rate of interchange of benzene and toluene between the liquid and vapour phases if resistance to mass lies in  film 0.50 mm thick.

Take atmospheric pressure=101 kN/m² and Universal gas constant G=8.314 kj/kg-mol K.

Solution:  

Example14.7 Derive an expression for the steady state diffusion of a gas A through another stagnant gas B.

Oxygen is diffusing through stagnant carbon monoxide at 0°C and 800 mm of Hg pressure under steady state conditions. The partial pressure of oxygen at two planes 0.6 cm apart is 100 mm of Hg and 20 mm of Hg respectively. Calculate the rate of diffusion of oxygen in gm-moles through cm² area. It may be presumed that:

Diffusivity of oxygen in carbon monoxide =0.185 cm²/s

Gas constant R=82.06 cm² atm/gm mole K.

Solution:    

Example14.8 Estimate the diffusion coefficient of carbon tetrachloride into air from the following data recorded in a Stefan-tube experiment with carbon tetrachloride and oxygen:

Diameter of tube and its length above liqid surface: 1 cm and 15 cm respectively

Temperature and pressure maintained: 0°C and 760 mm of mercury

Evaporation of carbon tetrachloride: 0.03 gm in 12 hour

Vapour pressure of carbon tetrachloride: 30 mm of mercury

Solution:    

Example14.9 An open tank, 10 mm in diameter, contains 1 mm deep layer of benzene (Mol wt =78) bottom. The vapour pressure of benzene in the tank is 13.15 kN/m² and its diffusion takes place through a stagnant air film 2.5 thick, At the operating temperature of 20°C, the diffusivity of benzene in the tank is 8.010^-6 m²/s. If the benzene has a density of 880 kg/m³, calculate the time taken for the entire benzene to evaporate. Take atmospheric pressure as 101.3 kN/m² and neglect any resistance to diffusion of beneze beyond the air film.

Solution: