Design of Structures 3(2+1)

LESSON 9. Design of Tension Member

9.2 STEPS TO BE FOLLOWED IN THE DESIGN OF A TENSION MEMBER

The following steps may be followed in the design of axially loaded tension members.

1. Corresponding to the loading on the structure of which the tension member is a part, the tensile force in the member is first computed.

2. The net area required for the member is determined by dividing the tensile force in the member by the permissible tensile stress.

3. Now, a suitable section having gross area about 20 per cent to 25 per cent greater than the estimated area is selected. For the member selected deductions are made for the area of rivet holes and the net effective area of the section is determined. If the net area of the section of the member so determined is greater than the net area requirement estimated in step i, the design is considered safe.

4. The slenderness ratio of a tension member shall not exceed 400. In the case of a tension member liable to reversal of stress due to the action of wind or earthquake, slenderness ratio shall not exceed 350. If the reversal of stress is due to loads others than wind or earthquake, the slenderness ratio shall not exceed 180.

Example 9.1: Determine the tensile strength of the 12 mm thick plate shown in Fig 9.1. Rivets used for the connection are 20 mm diameter. Allowable tensile stress is 150 N/mm².

Solution

Diameter of the rivet hole       = 20 + 1.5 = 21.5 mm

The critical section to be considered is a section like ABCDE.

Effective width at critical section           = b – nd = 180 – (3 x 21.5) = 115.5 mm

Effective net area                                 = 115.5 x 12 mm²              = 1386 mm²

Strength of plate                                  = 1386 x 150                      = 207900 N     = 207.9 kN.

Example 9.2: Find the strength of the 12 mm thick plate shown in Fig. 9.2. All the holes are 21.5 mm as gross diameter. Take f_t=150 N/mm².

 

Solution

Gross diameter of rivet hole   = 21.5 mm

The effective net width will be computed along the various chain lines

Staggered pitch        p = 40 mm

Gauge distance        g = 50 mm

Net width corresponding to the chain ABCD            = 210 – (2 x 21.5)       = 167 mm

Net width corresponding to the chain ABECFG

Example 9.3: The tension member of a roof truss consist of two unequal angles 70 x 45 x 8 with the longer legs connected by 16 mm diameter rivets. Find the safe tension for the member, the angles being one on either side of the gusset plate.

Solution

Gross area of 2 angles,            70 x 45 x 8      = 1,712 mm²

Area of 2 rivet holes   2 x (16 + 1.5) x 8         = 280 mm²

Net area of the member          1712 – 280      = 1,432 mm²

Therefore safe tension for the member           = 150 x 1432   = 2,14,800 N   = 214.8 kN.

Example 9.4: The tension member of a roof truss carries a maximum axial tension of 250 kN. Design the section. Diameter of connecting rivets = 20 mm. Safe stress in tension = 150 N/mm².

Solution

Referring to steel tables, let us choose two angles of I.S.A. 75 x 50 x 10 mm thick.

Gross area       = 75 mm x 50 mm x 10 mm    = 2,300 mm².

Let us assume that the angles are placed back to back on either side of the gusset plate (Fig. 9.3) with two rivets.

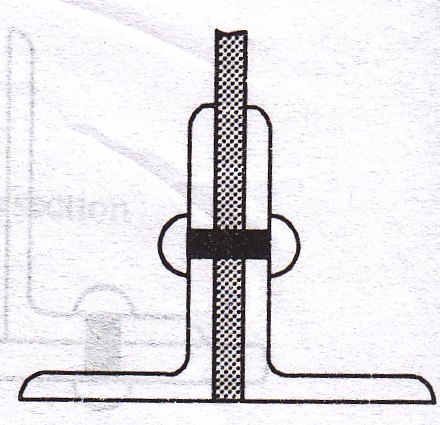
Diameter of rivet hole = 20 + 1.5 = 21.5 mm

Net area provided       = 2,300 – (2 x 21.5 x 10)        = 1,870 mm².

But the area required is only 1,667 mm². Hence the section is safe.

Example 9.5: The tie of a truss carries an axial tension of 225 kN. Design the section of the member and also the connection of the member to 10 mm thick gusset plate. Use 20 mm diameter rivets.

Solution

 

Example 9.6: The tie in a bridge truss carries an axial tension of 350 kN. The member is to consist of two channels connected back to back on either side of a gusset plate. The diameter of rivets used for the connection is 16 mm. Two rivets are likely to appear in section. Design the member. Safe stress in tension is 150 N/mm².

Solution

Net area required       

Referring to steel tables, let us select two channels ISLC, 125 (Fig. 9.5)

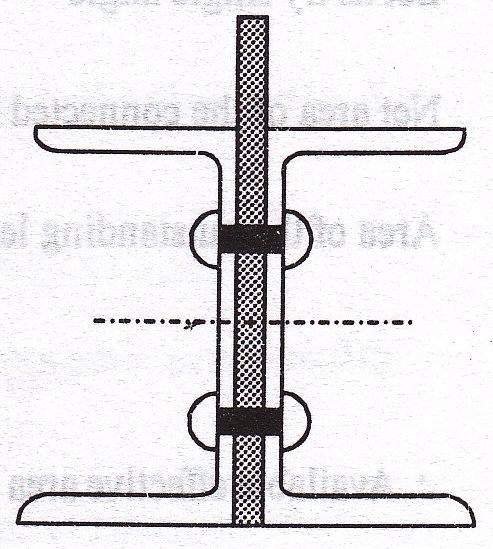
Dimensions of section                = 125 mm x 65 mm

                                    t_f          = 6.6 mm

                                    t_w         = 4.4 mm

Gross area                   A_g          = 1,367 mm² per channel

Diameter of rivet hole                 = 16 + 1.5        = 17.5 mm

Making allowance for four rive holes,

Net area provided                   = 2 x 1367 – (4 x 17.5 x 4.4)  = 2,426 mm².

But the required area is only 2,333 mm². Therefore, the section selected is safe.

Example 9.7: The tension member of a roof truss consist of a single ISA 100 x 75 x 10 mm thick, connected at the end to a gusset plate with the longer leg vertical with 20 mm diameter rivet. Find the safe tension the member can withstand. Permissible tensile stress may be taken as 150 N/mm².

Solution

Diameter of rivet hole             = 20 + 1.5        = 21.5 mm

Net effective area provided

Where, A₁ = Net sectional area of the connected leg,

            A₂ = Area of the unconnected leg, and

 Safe axial tension        = A_eff x Safe stress

                                    = 1,266 x 150  = 1,89,900 N   = 189.9 kN.

The tension member is shown in Fig. 9.6.

 

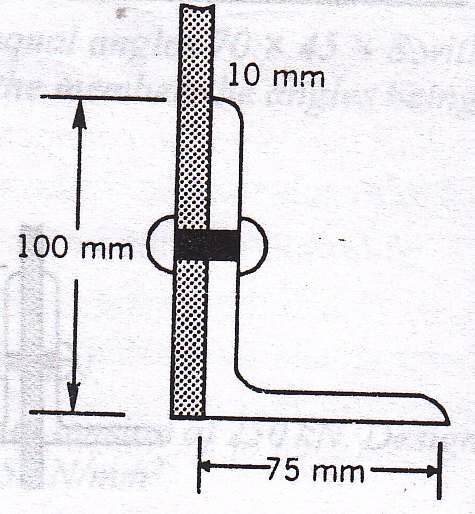
Example 9.8: Design a single angle tension member to sustain a tension of 1,30,000 N. Use 18 mm diameter rivets.

Solution

The single angle tension member is shown in Fig. 9.7.

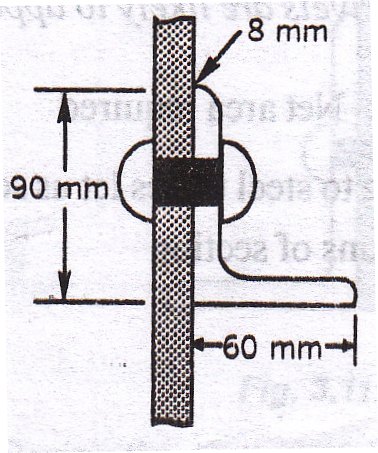
But actual tension in the member is only 1,30,000 N. Hence the design is safe.

Example 9.9: A tension member consist of two angles 60 x 60 x 8 the angles being placed back to back on the same side of the gusset plate. One leg of each angle is connected to the gusset plate. The outstanding legs are also connected by tack rivets. Find the safe tension for the member. Rivets are 16 mm in diameter.

Solution

The tension member is shown in Fig. 9.8.

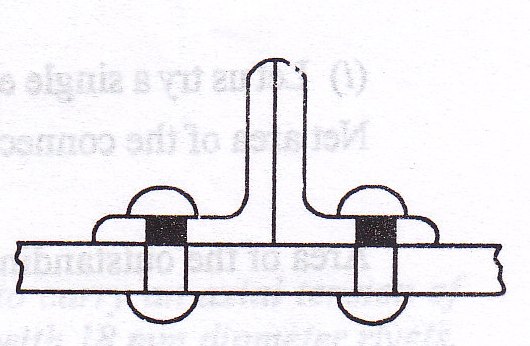
This being large the length of the connection can be decreased by using a lug angle,

Let the longer leg be the connected leg,

Area of the connected leg       = (125-5)10     = 1,200 mm²

Area of the outstanding leg    = (75-5)10       = 700 mm²

Therefore load taken by the connected leg    

Therefore load taken by the outstanding leg  = 200 – 126.3  = 73.7 kN

 Connection to the gusset plate using a lug angle is shown in Fig. 9.9.

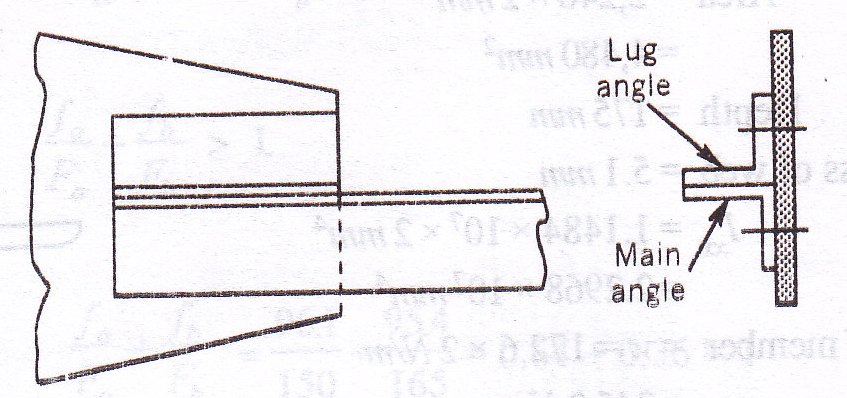
 The lug angle should have a strength equal to 20 % greater than the strength of the outstanding leg.

Therefore strength required for the lug angle = 1.2 x 73.7 kN           = 88.44 kN

Ne area required for the lug angle      = (88.44 x 1000/150)  = 589.6 mm²

Let us try 1 lug angle 125 x 75 x 6 mm

Gross area       = 1,166 mm²

Net area           = gross area – area of one rivet hole   = 1,166 – (21.5 x 6)    = 1,037 mm²

Strength required for connection between lug angle and the main angle is equal to 1.4 times the strength of the outstanding leg.

Therefore, strength required for this connection        = 1.4 x 73.7     = 103.18 kN

Number of rivets required = (103.18 x 1000/36,305) ≈ 3