Design of Structures 3(2+1)

LESSON 17. Design of Singly Reinforced Section

Type A Data:   Dimensions of the section, permissible stresses in concrete and steel, area of tensile steel and modular ratio.

Required: Moment of resistance of the section.

This type of problem may be solved as follows:

1. First determine the position of the actual neutral axis by equating the moment of the concrete area in compression about the neutral axis to the moment of equivalent tension area about the neutral axis i.e. use the relation,  

2. Find the position of critical neutral axis corresponding to the given safe stresses in concrete and steel.

3. Ascertain whether the section is under-reinforced or over-reinforced. If the actual neutral axis lies above the critical neutral axis, the section is under-reinforced. But, if the actual neutral axis is below the critical neutral axis, the section is over-reinforced

4. If the section is over-reinforced concrete attains its permissible stress earlier than steel, and the moment of resistance is given by

Taking,                        c = = permissible stress in concrete

and                                       n = depth of actual neutral axis.

If the section is under-reinforced, steel attains its permissible stress earlier than concrete and the moment of resistance is given by

                                                M.R. =   

taking,                                     t =  =  permissible stress in steel

and                                                n  = depth of actual neutral axis.

Type B Data : Dimensions of the section, Area of reinforcement, Bending moment M and modular ratio.

Required : Stresses in concrete and steel.

This type of problem may be solved as follows:

1. Determine the position of the actual neutral axis.

2. Find the stress in concrete by equating the moment of resistance to the given bending moment i.e., use the relation,

3. Find the stress in steel from the relation.

 

Type C Data : Permissible stresses in concrete and steel, Bending moment M and modular ratio.

Required: To design the section.

This type of problem may be solved as follows: The beam will be designed as a balanced section

1.Determine the depth of critical neutral axis in terms of the effective depth d.

2. Choose a convenient width b. By equating the moment of resistance to the given bending moment, find the effective depth

3. Find the area of steel by equating the total compression on the beam section to the total tension on the beam section.

The following problems illustrate the above types of problems.

 

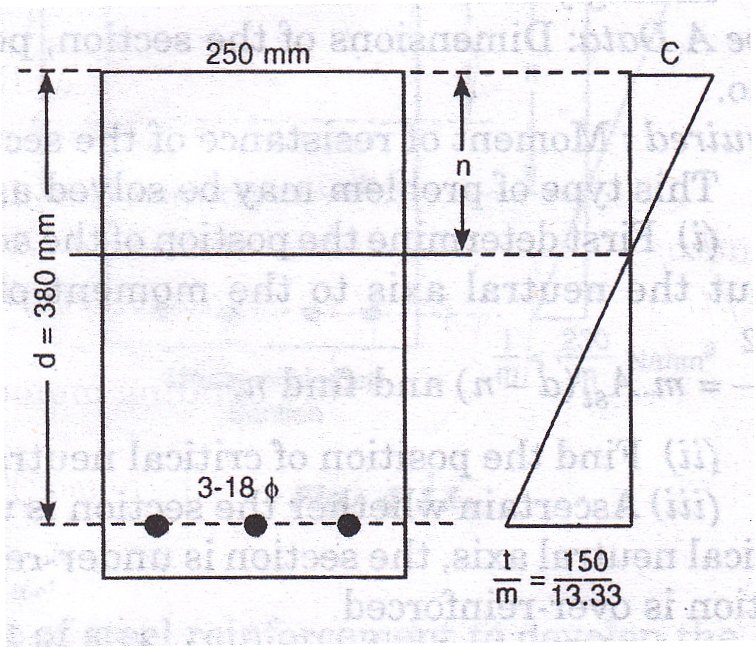
Example 17.1 A singly reinforced beam 250 mm wide and 380 mm deep to the centre of reinforced with 3 bars of 18 mm diameter. Determine the depth of neutral axis and the maximum stress in concrete when the stress in steel is 150 N/mm². Take m = 13.33.

Solution.

Position of neutral axis (see Fig. 17.1)

 

Example 17.2 The cross-section of a singly-reinforced concrete beam is 300 mm wide and 400 mm deep to the centre of the reinforcement which consists of three bars of 12 mm diameters. If the stresses in concrete and steel are not to exceed 7 N/mm² and 230 N/mm², determine the moment of resistance of the section. Take m =13.33

Solution.         Area of steel  

Position of actual neutral axis (see Fig. 17.2)

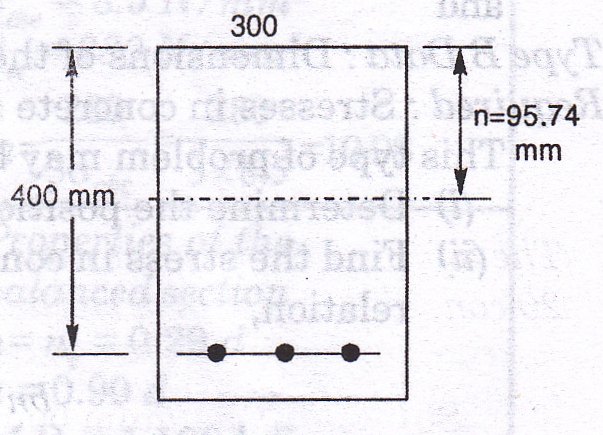
Taking moments about the neutral axis,

Example 17.3 The cross-section of a singly-reinforced concrete beam is 300 mm wide and 400 mm deep to the centre of the reinforcement which consists of four bars of 16 mm diameter. If the stresses in concrete and steel are not exceed 7 N/mm² respectively, determine the moment of resistance of the section. Take m = 13.33.

Solution.                            

Position of actual neutral axis (see Fig. 17.3)

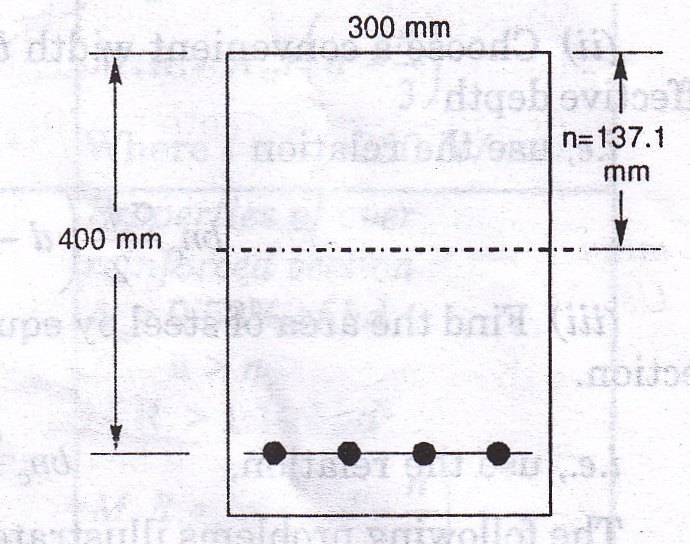
Taking moments about the neutral axis         

 

Example 17.4 A singly-reinforced rectangular beam 350 mm wide has a span of 6.25 m and carries an all inclusive load of 16.30 kN/m. If the stresses in concrete and steel shall not exceed 7 N/mm² and 230 N/mm² find the effective depth and the area of the tensile reinforcement. Take m=13.33.

                             

 Example 17.5 A singly reinforced beam has a span of 5 meters and carries a uniformly distributed load of 25 kN/m. The width of the beam is chosen to be 300 mm. Find the depth and the steel area requited for a balanced section. Use M 20 concrete and Fe415 steel

Solution Maximum bending moment M =  = 78.125 kNm

The section is a balanced section (see Fig. 17.4).

Equating balanced M.R. to bending moment

0.913 bd² = 0.913 x 300 d² = 78.123 x 10⁶

Therefore                                     d = 534 mm

Area of steel required =   = 706.7 mm²

Provide 2 bars of 18 mmΦ and 1 bar 16 mmΦ 

Area of steel provided = 2 (254) + 201 = 709 mm²

Overall depth of the beam = 534 + 9 + 25 = 568 mm

Let us provide an overall depth of 570 mm

Actual effective depth = 570-34 = 536 mm

Example 17.6 Design a singly reinforced beam section subjected to a maximum bending moment of 55.35 kNm. The width of the beam may be made two third the effective depth. Use M 20 concrete and Fe415 steel.

Provide b = 300 mm, d = 450 mm

Provide 3 bars of 16 mm of (603 mm²)

Example 17.7 A singly-reinforced concrete beam is 300 mm wide and 450mm deep to the centre of the tensile reinforcement which consists of 4 bars of 16 mm diameter. If the safe stresses in concrete and steel are 7 N/mm² and 230 N/mm² respectively, find the moment of resistance of the section. Take m = 13.33._­

Solution.

                                    b = 300 mm, d =450 mm

                                     = 4 x 201 = 804 mm²

Depth of actual Neutral axis

                                   

            Therefore                      = 129.9 mm

Depth of actual Neutral axis,

Taking moments about the neutral axis,

Since n>n_c the section is over reinforced

            Therefore Concrete attains its safe stress earlier to steel.

            Moment of resistance  =

Example 17.8 A singly-reinforced concrete beam 350 mm wide and 550mm deep to the centre of the tensile reinforcement is reinforced with 3 bars of 18 mm diameter. Find the moment of resistance of the section. What would be the moment of resistance if the reinforcement is changed to 4 bars of 18 mm diameter. Use M 20 concrete and Fe 415 steel.

Solution.         Safe stresses σ_{cbc =} 7 N/mm², σ_st = 230 N/mm²

Modular ratio,                      

Depth of critical Neutral axis

Case (i) When 3 bars of 18 mm diameter are provided

                                                 = 3 x 254 = 762 mm²

Position of actual neutral axis

Taking moments about the neutral axis

                                              

                        n² + 58.057 n – 31931.429 = 0

                                                n = 152mm      But, n_c = 158.8 mm

Since n< n_c the section is under-reinforced.

Therefore Steel reaches its safe stress earlier to concrete.

Moment of resistance  = 

                                     =     87.513 x 10⁶  Nmm = 87.513 kNm

Case(ii) When 4 bars of 18 mm diameter are provided

                                     = 4 x 254 = 1016 mm²

Taking moments about the neutral axis,

                                   

n² + 77.409n – 42575.24 = 0

Therefore         n = 171.2 mm But n_c = 158.8 mm

Since,  n > n_c the section is over reinforced

Therefore Concrete reaches its safe stress earlier to steel

Moment of resistance             

                                                = 103.394 x 10⁶  Nmm = 103.394 kNm

Example 17.9 A singly- reinforced concrete beam 300 mm wide has an effective depth of 500 mm, the effective span being 5 m. It is reinforced with 804 mm² of steel. If the beam carries a total load of 16 kN/m on the whole span, determine the stresses produced in concrete and steel. Take m = 13.33.

Solution. Maximum B.M. for the beam =   = 50 kNm

Position of neutral axis

Taking moments about the neutral axis,

                                                             = 13.33 x 804 (500 – n)

                             n² + 71.4488n – 35724.4 = 0

Therefore                                                     n= 156.63 mm

                                  Moment of resistance = Bending moment

                    

                                                               c =    = 4.75 N/mm²

           Stress in steel =   N/mm²

                                  = 138.80 N/mm²

Example 17.10 A singly-reinforced beam 350mm wide and 550mm deep has an effective span of 6 m and carries an all inclusive load of 20 kN/m. The beam is reinforced with 4 bars of 20 mm diameter at an effective cover of 35 mm. Find the maximum stresses produced in concrete and steel. Take m = 13.33.

Solution. Area of steel                         = 4 x 314 = 1256 mm²

Maximum B.M.                                         = = 90 kNm = 90 x 10⁶ Nmm

Position of actual neutral axis

Effective depth                                   d = 550 – 35 = 515 mm

Taking moments about the neutral axis,

                                                            

                               n² + 95.67n – 49270.7 = 0

Solving, we get                                     n = 179.23 mm

Let the maximum compressive stress reached in concrete be c N/mm²

Equating M.R. to the B.M.

           

                                                               c = 6.30 N/mm²

Stress in steel                                       

Example 17.11 Find the moment of resistance of a singly reinforced beam section 225 mm wide and 350 mm deep to the centre of the tensile reinforcement if the permissible stresses in concrete and steel are 230 N/mm² and 7N/mm². The reinforcement consists of 4 bars of 20 mm diameter. What maximum uniformly distributed load this beam can safely carry on a span of 8 m? Take m = 13.33

Solution

                                   

Taking moments about the neutral axis (see Fig. 17.5),

                                    

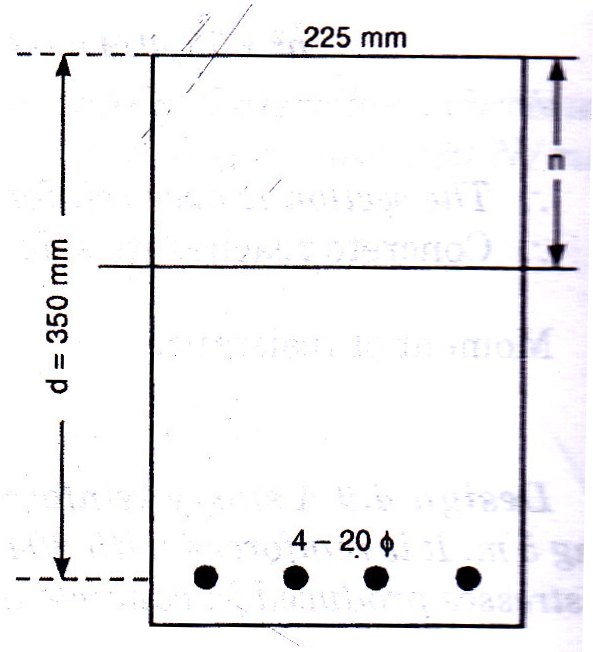
Therefore                     n² + 148.893n – 52112.598 = 0

Therefore                     n = 165.67

The depth of critical neutral axis is given by

                                    

Since n > n_c, the beam section is over reinforced.

Therefore Concrete reaches its permissible stress earlier to steel.

Moment of resistance

                                           

                                                = 38458075 Nmm = 38.458 kNm

                                           w = safe uniformly distributed load on the beam

Let maximum bending moment