Mechanics of Tillage and Traction 3(2+1)

LESSON 16. Methods of dimensional analysis

16.1 Rayleigh Method

As early as 1899, Lord Rayleigh made an ingenious application of dimensional analysis to the problem of the effect of temperature on the viscosity of gas. Rayleigh’s method is outwardly different from Buckingham’s method; let us consider the drag force F that a smooth spherical body experiences in a stream of incompressible fluid. Consider tentatively a relationship of the form,

                                    F = V^aD^br^cm^d             ------------------------------------ (3.1)

The exponents must be adjusted to make the equation dimensionally homogeneous. This leads to the more special form

                                 F =rV²D²Rⁿ                   ------------------------------------ (3.2)

Where R = VDr/m and n is a numerical exponent.

Equation (3.1) is of such of restricted form that can be expected to represent the phenomenon. However, Rayleigh pointed out that special solutions of the type of the equation b may be summed to give more general solutions. Accordingly a general type of dimensionally homogeneous relationship is

                                            F =rV²D²åA_nRⁿ  

In which the coefficients A_n are dimensionless constants. Since the series is a general function of R, the solution is of the form,

                                           F =rV²D²f(R)

in which f is an unspecified function.

16.2 Buckingham’s Pi theorem

Evidently, any equation that relates dimensionless products is dimensionally homogeneous; i.e. the form of the equation does not depend on the fundamental units of measurement. This observation may be formally stated as follows:

A sufficient condition that an equation be dimensionally homogeneous is that it be reducible to an equation among dimensionless products.

E. Buckingham inferred the fundamental principle that the conditions of this theorem are also necessary. Buckingham’s theorem is accordingly stated as follows:

‘If an equation is dimensionally homogeneous, it can be reduced to a relationship among a complete set of dimensionless products’.

In other words, “Any equation that relates dimensionless product is dimensionally homogeneous. The condition that an equation be dimensionally homogeneous is to an equation among dimensionless products”.

This theorem is, by no means, self- evident. Buckingham himself did not rigorously prove the theorem, although he presented evidence to make its truth seem plausible.

Buckingham’s theorem summarizes the entire theory of dimensional analysis. However, principles of dimensional analysis were employed before this theorem was expounded.

Let us now consider the problem in 3.1 in the light of Buckingham’s theorem. We assume only that the five variables are related by a dimensionally homogeneous equation. This may be indicated by f(F,V,D,ρ,μ) = 0, in which f is an unspecified function.

The Buckingham’ theorem states that if there are n dimensional variables involved in a phenomenon, which can be completely described by m fundamental quantities or dimensions (such as mass, length, time etc.,) and are related by a dimensionally homogeneous equation, then the relationship among the n quantities can always be expressed in terms of exactly (n-m) dimensionless and independent p terms.          

16.2.1 Procedure for Buckingham’s Pi method

a. List all the ‘n’ physical quantities or variables involved in the phenomenon. Note their dimensions and the number ‘m’ of the fundamental dimensions comprised in them. So that there will be (n-m). π terms.

b. Select ‘m’ variables out of these to serve as repeating variables with the following guidelines:

i. These variables should be such that none of them is dimensionless.
ii. No two variables have the same dimensions.
iii. They themselves do not form a dimensionless parameter.
iv. The entire ‘m’ fundamental are included collectively in them.
v. The dependent variable should not be taken as repeating variable.

c. Write the general equations for different π terms. These may be expressed as the product of the repeating variables each raised to an unknown exponent and one of the remaining variables taken in turn, with a known power (usually taken as one).

d. Write the dimensional equations of the equations of the π terms obtained in the step (c) above.

Compute the value of the unknown exponents by equating the exponents of the respective fundamental dimensions on both the sides of each of the dimensional equations. Thereby different dimensional groups or π terms are formed.

e. Write the final general equation for the phenomenon in terms of the π terms.

In order to obtain the final expression the following additional may be considered

i. If the quantity is dimensionless, it is a π term with out going through the above procedure.

ii. If any two physical quantities have the same dimensions, their ratio will be one of the π term. For example (H/d) is dimensionless and hence it is a π term.

iii. Any π term may be replaced by any power of that term, including negative as well as fractional powers. For example, π₁ may be replaced by π^-1, or π₂ may be replaced by π₂², or π₃ may be replaced by   etc.

iv. Any π term may be replaced by multiplying it by numerical constant. For example, π₁ may be replaced by 3π₁ or so.

v. Any π term may be replaced by another π term obtained by adding or subtracting an absolute numerical from it.

vi. Any π term may be replaced by multiplying it by another π term. For example, π₁ may be replaced by (π₁ x π₂).

Mathematically, if any variable Q₁ depends on the independent variables Q₂, Q₃, Q₄……Q_n, ; the fundamental equation may be written as,

                                    Q₁= f (Q₂, Q₃, Q₄……Q_n)

which can be transformed to another functional relationship as,

                        f₁ (Q_1, Q₂, Q₃, Q₄……Q_n) = C

where ‘C” is the dimensionless constant.

In accordance with the π theorem, a non dimensional equation can thus be obtained in the form,

                                    f₂ (π₁, π₂, π₃,……..π _n-m)            =        C₁

wherein, each dimensionless π-term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variables. These ‘m’ variables which appear repeatedly in each of the π terms, are called repeating variables. These are ‘m’ fundamentals quantities. They themselves do not form a dimensionless parameter. Thus the different π terms may be established as,

                                    π₁            =         Q₁^a1_, Q₂^b1, Q₃^c1….. Q_m^m1 Q_m+1

                                                π₂            =         Q₁^a2_, Q₂^b2, Q₃^c2….. Q_m^m3 Q_m+2

                                    …………………………………………..

                                    π_n-m        =         Q₁^an-m_, Q₂^{b n-m}_, Q₃^{c n-m}_,….. Q_m^{m n-m}_, Q_n

In the above equation, each individual equation is dimensionless and the exponents a, b, c, d …….. m etc are determined by considering dimensional homogeneity for each equation such away that each π term is dimensionless.

The final general equation for the phenomenon may then be obtained by expressing any one of the π terms as a function of the others.

                        π₁            =          f₁ (π₁, π₂, π₃,……..π _n-m)

                        π₂            =          f₂ (π₁, π₂, π₃,……..π _n-m)

or any other desired relationship may be obtained.

The use of Buckingham’s Pi method is illustrated by an example.

Consider the problem of drag force that a smooth spherical body experiences in a stream of compressible fluid. Assume that five variables namely, drag force (F), velocity (V), diameter of sphere (D), density of fluid (ρ) and absolute viscosity (μ), are related by a dimensionally homogeneous equation. This may be indicated by

F =f( V, D, ρ , μ ).

This may be written in the general form 

            f₁ (F, V, D,ρ,μ )  = C

The total number of variables,n = 5

These variables may be completely described by three fundamental dimensions of M – L – T (m = 3 fundamental unit).

Therefore the number of π terms = n-m = 5 - 3 = 2 (ie., Number of π terms is 2)

                                             f₂ (π_1, π₂)           =        C₁

In order to form these π terms, choose the three repeating variables following the guidelines, since the fundamental dimensions are three. Choose r, V and D as repeating variables. Since physical quantities of the similar dimensions can neither be added nor subtracted the terms are expressed as products as follows:

                        π₁         =         r^a1V^b1D^c1m       ----------------------------------- (3.3)          

                        π₂            =         r^a2V^b2D^c2F       ----------------------------------- (3.4)

 Expressing π₁ dimensionally in terms of M- L - T, we get

\[{\left( {{M \over {{L^3}}}} \right)^{a1}}{\left( {{L \over T}} \right)^{b1}}{\left( L \right)^{c1}}{\left( {{M \over {LT}}} \right)^{}} = {M^0}{L^0}{T^0}\]

Equating the exponents of M, L, and T, we get

For M:             a₁ + 1 = 0;  \ a₁ = -1               ------------------------------------ (3.5)

For L:              -3 a_{1 +} b₁ +c₁ -1 =0                ------------------------------------ (3.6)

For T:              -b₁ -1 = 0;   \ b₁ = -1              ------------------------------------ (3.7)

Substituting the value of ‘a₁ & b₁’ in equation 3.5 and ‘e’ in equation 3.6, we get

3-1+ c₁ -1= 0:  c₁ = -1

Substituting the values of a₁, b₁, and c₁ in equation 3.3, we get

                                           

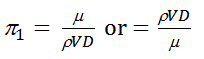
Similarly,

                        π₂ = ρ^a2V^b2D^c2F

Expressing π₁ dimensionally in terms of M-L-T, we get

\[{\left( {{M \over {{L^3}}}} \right)^{a2}}{\left( {{L \over T}} \right)^{b2}}{\left( L \right)^{c2}}\left( {{{ML} \over {{T^2}}}} \right) = {M^0}{L^0}{T^0}\]

Equating the exponents of M, L, and T, we get

For M:             a₂ + 1 = 0;        \ a₂ = -1         ------------------------------------ (3.8)

For L:              -3 a_{2 +} b₂ +c₂ +1 = 0              ------------------------------------ (3.9)

For T:              -b₂ -2 = 0;        \ b₂ = -2         ------------------------------------ (3.10)

Substituting the value of a₂ & b₂ in equation 3.8 and 3.10 in equation 3.9, we get

3-2+ c₂ +1= 0:             c₂ = -2

Substituting the values of a₂, b₂, and c₂ in equation 3.4, we get

                       

Buckingham’s theorem asserts that, since the equation is dimensionally homogeneous, f is not actually a function of five separate variables, but rather a function of a complex set of dimensionless products of the variables is comprised of the pressure coefficient, P = Fρ^-1V^-2D^-2, and the Reynolds number, R = VDρμ^-1. Hence, by Buckingham’s theorem, the equation is reducible to the form, f (P,R) = 0. This relationship may be indicated in the explicit form, P = f(R). If f is regarded merely as a symbol for some function, the relationships, f (P, R) = 0 and P = f(R), mean the same thing; namely, that is possible to plot a curve that shoes the relation ship between P and R. The equation, P = f(R), is same result that was obtained above, by Rayleigh’s method. The reasoning that has led to the conclusion, P = f(R), is not restricted to spherical bodies, it is valid for a body of any shape. Example: airplane wing. The form of the curve that relates P to R depends, of course, on shape of the body. Dimensional analysis provides no information concerning the form of the curve.

Rayleigh’s method of dimensional analysis does not differ intrinsically from Buckingham’s method. The algebraic steps in two methods are essentially same. However, Buckingham’s method absolves us from the indiscriminate use of infinite series. Too often, it is not explained that the construction of an infinite series is a logically indispensable step in Rayleigh’s method. Consequently, the impression is created that the dependent variable in a physical problem may be arbitrarily equated to a product of powers of the independent variables and a numerical coefficient. This assumption is sometimes a legitimate approximation, particularly in problems of heat transfer, but it is not essential part of dimensional analysis.

If n variables are connected by unknown dimensionally homogeneous equation, Buckingham’s theorem allows up to conclude that the equation can be expressed in the form of a relationship among (n – m) dimensionless products, in which (n – m) is the number of products in a complex set of dimensionless products of the variables.  In most cases, m is equal to the number of fundamental dimensions in the problem.  However, this cannot be an infallible rule, since the number of fundamental dimensions in a problem may depend on the system of fundamental dimensions that is used.