Soil Mechanics 3(2+1)

LESSON 2. Phase Diagram

2.2 Definitions

Void Ratio

Void ratio (e) of a soil is the ratio of the volume of voids to the volume of solid. Thus,

\[e={{{V_v}} \over {{V_s}}}\]                    (2.1)

The void ratio is greater than zero (as soil has to contain some voids), but there is no upper limit to the value of void ratio. As this the ratio of two volumes, it is unit less.   

 

Porosity

The porosity (n) of a soil is the ratio of the volume of voids to the total volume of the soil. Thus,

\[n={{{V_v}} \over V} \times 100\]                      (2.2)

The porosity cannot be greater than 100%. As this the ratio of two volumes, it is unit less.

 

Water content

The water content or moisture content (w) of a soil is the ratio of weight of water to the weight of solids present in the soil. Thus,

\[w={{{w_w}} \over {{w_s}}} \times 100\]                      (2.3)

The water content is greater than or equal to zero, but there is no upper limit to the value of water content. As this the ratio of two weights, it is unit less.

 

Degree of saturation

The degree of saturation (S) is the ratio of the volume of water to the volume of voids. Thus,

\[S={{{V_w}} \over {{V_v}}} \times 100\]                           (2.4)

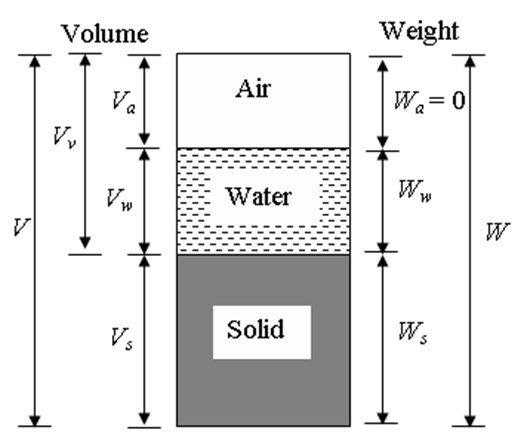
(a) Partially saturated soil (Three-phase system)

 (b) Completely saturated soil (Two-phase system)

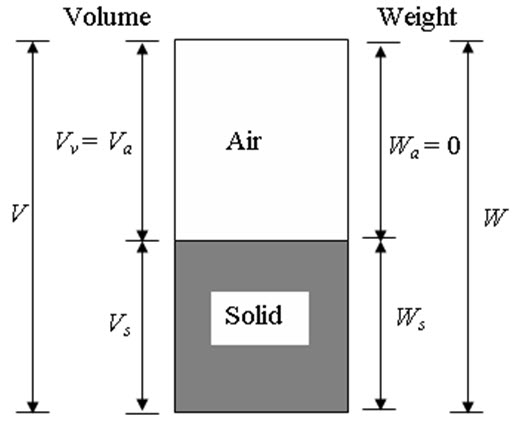
(b) Completely dry soil (Two-phase system)

Figure 2.1. Phase diagrams.

For fully saturated soil, V_v = V_w, Thus, S = 100% or 1. Similarly, for completely dry soil, V_w = 0, Thus, S = 0. For partially saturated soil, S value can be in between 0 to 100%. As this the ratio of two volumes, it is unit less.

 

Unit weight

Depending upon the state of the soil, the unit weight of the soil also changes. Bulk unit weight ( \[{\gamma _{bulk}}\] or \[{\gamma _t}\] ) of the soil is defined as the total weight of the soil mass per unit of total volume. The bulk unit weight is the unit weight of the soil in its natural condition. In SI unit, it is expressed as ‘kN/m³’. Thus,

\[{\gamma _t}={W \over V}={{{W_s} + {W_w}} \over {{V_s} + {V_w} + {V_a}}}\]                  (2.5)

Saturated unit weight  ( \[{\gamma _{sat}}\] ) of the soil is defined as the total weight of the soil when it is fully saturated per unit of total volume. This is the unit weight of soil under completely saturated condition. Thus,

\[{\gamma _{sat}}={{{W_{sat}}} \over V}\]                     (2.6)

Dry unit weight ( \[{\gamma _d}\]  ) of the soil is defined as the weight of soil solids per unit of total volume. This is the unit weight of soil under completely dry condition. Thus,

\[{\gamma _d}={{{W_s}} \over V}\]                                 (2.7)

Submerged unit weight ( \[\gamma '\] ) of the soil is equal to the saturated unit weight of soil minus unit weight of the water ( \[{\gamma _w}\] ). The unit weight of water is taken to be 9.8 kN/m³ or approximately 10 kN/m³. Thus,

Unit weight of solids ( \[{\gamma _s}\] ) is the ratio of weight of solid to the volume of solids. Thus,

\[{\gamma _s}={{{W_s}} \over {{V_s}}}\]            (2.9)

Specific gravity

The specific gravity (G_s) of the soil is defined as the ratio of the weight of a given volume of solid to the weight of an equivalent volume of water at 4°C. Thus,

\[{G_s}={{{W_s}} \over {{V_s}{\gamma _w}}}={{{\gamma _s}} \over {{\gamma _w}}}\]                  (2.10)

The specific gravity of the soil varies in between 2.65 to 2.80 (Ranjan and Rao, 2000). Specific gravity is also a unit less quantity.

2.3 Important Relationships

Followings are the important relationships between the various quantities defined in the previous section.

\[n={e \over {1 + e}}\]                          (2.11)

\[{V_s}={V \over {1 + e}}\]                (2.12)

\[{V_v}={e \over {1 + e}}V\]              (2.13)

\[e={{{G_s}w} \over S}\]                    (2.14)

\[{\gamma _{bulk}}={\gamma _t}={{{G_s} + Se} \over {1 + e}}{\gamma _w}\]                 (2.15)

For completely saturated soil, S =1, Thus,

\[{\gamma _{sat}}={{{G_s} + e} \over {1 + e}}{\gamma _w}\]                          (2.16)

For completely dry soil, S =0, Thus,

\[{\gamma _d}={{{G_s}} \over {1 + e}}{\gamma _w}\]                                       (2.17)

\[\gamma '={{{G_s} - 1} \over {1 + e}}{\gamma _w}\]                                         (2.18)

\[{\gamma _d}={{{\gamma _{bulk}}} \over {1 + w}}\]                                         (2.19)

Problem 1: In a partially saturated soil, moisture or water content is 20% and \[{\gamma _{bulk}}\] = 18 kN/m³. Determine the degree of saturation and void ratio. G_s = 2.65. Take the unit weight of the water as 10 kN/m³.

Solution: 

\[{\gamma _d}={{{\gamma _{bulk}}} \over {1 + w}}={{18} \over {1 + 0.2}} = 15\;kN/{m^3}\]

\[{\gamma _d}={{{G_s}} \over {1 + e}}{\gamma _w}\]

Thus, \[e={{{G_s}{\gamma _w}} \over {{\gamma _d}}}-1={{2.65 \times 10} \over {15}}-1=0.767\]

Thus, the void ratio is 0.767.

\[e={{{G_s}w} \over S}\]

Thus, \[S={{{G_s}w} \over e}={{2.65 \times 0.2} \over {0.77}}=0.691\]

Thus, the degree of saturation is 69.1%.

 

References

Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

 

Suggested Readings

Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.

Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.