System Engineering 3(3+0)

Lesson 4 Solved Examples

Solution

From the data of the problem, we have

                  λ  = 10/8 = 5/4 sets per hour;  and μ = (1/30) 60 = 2 sets per hour

(a)  Expected idle time of repairman each day = Number of hours for which the repairman remains busy in an 8-hour day (traffic intensity) is given by

(8) (λ/μ) = (8) (5/8) = 5 hours

Hence, the idle time for a repairman in an 8-hour day will be: (8 – 5) = 3 hours.

(b) Expected (or average) number of TV sets in the system

 

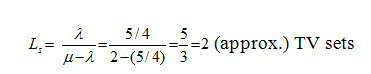
Example2   On an average 96 patients per 24-hour day require the service of an emergency clinic. Also on an average, a patient requires 10 minutes of active attention. Assume that the facility can handle only one emergency at a time. Suppose that it costs the clinic Rs 100 per patient treated to obtain an average servicing time of 10 minutes, and that each minutes of decrease in this average time would cost Rs. 10 per patient treated. How much would have to be budgeted by the clinic to decrease the average size of the queue from one and one-third patients to half patient.

 

Solution     From the data of the problem, we have

                  

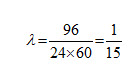
                    and    patients per minute; 

(i)Average number of patients in the queue

 

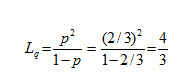
(ii)Fraction of the time for which there no patients,

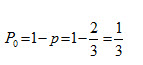
(iii)When the average queue size is decreased from 4/3 patient, the new service rate μ is determined as:

  patients per minute.

Average rate of treatment required is: 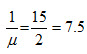minutes, i.e.  a decrease in the average rate of treatment is 2.5(= 10 – 7.5) minutes.

 

Budget per patient = Rs (100 + 2.5 x 10) = Rs 125 per patient.

 

Example 3  Customers arrive at a one-window drive according to a Poisson distribution with mean of 10 minutes and service time per customer is exponential with mean of 6 minutes. The space in front of the window can accommodate only three vehicles including the serviced one. Other vehicles have to wait outside this space. Calculate:

 (a)  Probability that an arriving customer can drive directly to the space in front of the window.

(b) Probability that an arriving customer will have to wait outside the directed space.

(c)  How long an arriving customer is expected to wait before getting the service?

 

Solution     From the data of the Problem, we have =6 customers per hour; = 10 customers per hour

 (a)  Probability that an arriving customer can drive directly to the space in front of the window:

 

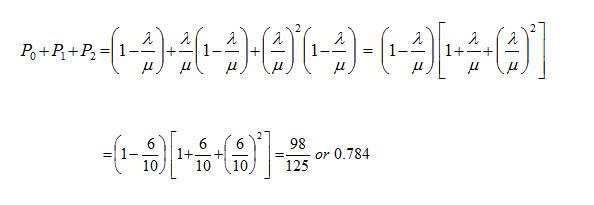
 (b) Probability that an arriving customer will have to wait outside the directed space:

 

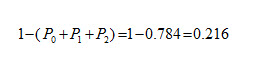
(c)  Expected waiting time of a customer before getting the service is:

 

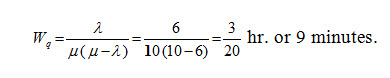
Example 4:  Students arrive at the head office according to a Poisson input process with a mean rate of 40 per hour. The time required to serve a student has an exponential distribution with a mean of 50 per hour. Assume that the students are served by a single individual, find the average waiting time of a student.

Solution.

Given,    λ = 40/hour,     μ = 50/hour

Average waiting time of a student before receiving service 

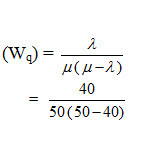
            = 4.8 minutes                                                                                       

 

Example 5: New Delhi Railway Station has a single ticket counter. During the rush hours, customers arrive at the rate of 10 per hour. The average number of customers that can be served is 12 per hour. Find out the following:

• Probability that the ticket counter is free.
• Average number of customers in the queue.

Solution.

Given
   λ  = 10/hour,       μ= 12/hour

Probability that the counter is free  =	1 -	10 ----- 12	=	1/6
Average number of customers in the queue (Lq ) =	(10)2 -------- 12 (12 - 10)		=	25/6

 

 

Example 6: Universal Bank is considering opening a drive in window for customer service. Management estimates that customers will arrive at the rate of 15 per hour. The teller whom it is considering to staff the window can service customers at the rate of one every three minutes.

Assuming Poisson arrivals and exponential service find

1. Average number in the waiting line.
2. Average number in the system.
3. Average waiting time in line.
4. Average waiting time in the system.

Solution.

Given, λ  = 15/hour,  μ= 3/60 hour  or  20/hour

 

Average number in the waiting line =	(15)2 ---------- 20(20 - 15)	=	2.25 customers
Average number in the system =	15 ---------- 20 - 15	=	3 customers
Average waiting time in line =	15 ------------ 20(20 - 15)	=	0.15 hours
Average waiting time in the system =	1 --------- 20 - 15	=	0.20 hours