System Engineering 3(3+0)

LESSON 1. Project cost and Resource Leveling

PROJECT COST

In order to include the cost aspects in project scheduling, we must first define the cost-duration relationships for various activities in the project. The total project cost comprises direct and indirect costs. The direct costs are associated with the individual activities such as manpower loading, equipment utilized, materials consumed directly, etc., in respect of various activities. The indirect costs are those expenditures which cannot be allocated to individual activities of the project. These may include administration or supervision costs. loss of revenue, fixed overheads, depreciation, insurance, and so on. While indirect cost allocated to a project goes up with the increase in project duration, direct costs go high as the time for individual activity is reduced. Such deliberate reduction of activity times by putting an extra effort is called crashing the activity.

It may be noted that for technical reasons, the duration of an activity cannot be reduced indefinitely. The crash time represents the fully expedited or the minimum activity duration time that is possible, and any attempts to further 'crash' would only raise the activity direct costs without reducing the time. The activity cost corresponding to the crash time is called the crash cost which equals the minimum direct cost required to achieve the crash performance time. These are in contrast to the normal time and the normal cost of the activity. The normal cost is equal to the absolute minimum of the direct costs required to perform an activity. The corresponding activity duration is known as the normal time.

The direct cost-time relationship and indirect cost-time relationships are

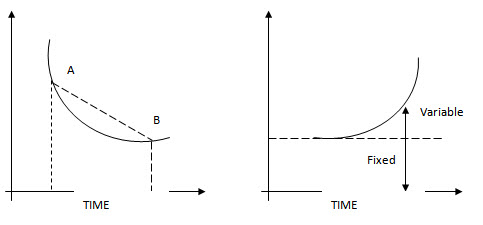
The point A in denotes the normal time for completion of an activity whereas point B denotes the crash time which indicates the least duration in which the particular activity can be completed. The cost curve is non-linear and asymptotic but for the sake of simplicity it can be approximated by a straight line with its slope given by

 

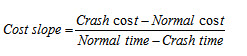
The cost slope represents the rate of increase in the cost of performing the activity per unit decrease in time and is called cost/time trade off. It varies from activity to activity. Having assessed the direct and indirect project cost the total costs can be found out. The total project cost is the sum total of the project ­direct and indirect costs.

Shows both the direct and the indirect project cost. As these two curves have been plotted against the same time scale, at each ordinate, the project direct and indirect costs can be added to obtain the various points on the graph, indicating the total project cost corresponding to the various project durations. If these total time-cost points are joined to form a curve, the curve so obtained will be total project cost curve. If this curve is examined carefully, it may be seen that for different project durations, there will be corresponding project costs. However, compared to all other points on this curve, there will be one point which is at the lowest, indicating the least cost and the minimum time for the project. It may again be observed that any point on the right hand side of this lowest point, the cost of the project increases and project duration also increases. On the other hand, if the point~ on the left hand side of the lowest point of this curve is considered, it may be seen that though there is reduction in project duration time, the cost of the project, however, increases. So much so, any point either on the right hand side or left hand side of the lowest point of this total projects. cost curve, it is not advantageous to the project manager to choose any of the points for the implementation of the project Obviously, it is the lowest point which indicates the lowest overall cost against the minimum time required for the completion of the project. This point may therefore be called as the optimum time-cost point of the curve which the project manager can choose for the implementation of the project

RESOURCE LEVELLING

In PERT and CPM techniques there is an implied assumption that required resources are always available. When resources are limited, two alternative courses of action are available. In the first alternative, the activities are critically sequenced and the minimum period of project is redetermined. This process is called Resource Levelling. The problem here is to manipulate the activity slacks, schedules and resource requirements throughout the duration of the project.

In resource levelling two types of problems are involved:

1. Levelling resource demands with constraint on the total project duration time.

2. Minimization of the project duration time with a constraint on the total availability of certain key resources.

The first problem arises when resources are adequate but they are desired to be used at a relatively constant rate during the life of the project. The second problem occurs when the resources cannot be increased and the object is to minimize project duration with available resources.

Thus, resource levelling or load levelling is required when the demands on specified resources are required not to exclude the specified level and the duration of the project is not invariant.

Remark. In order to stabilize the use of existing level of resources the total float of non-critical activities is used. By shifting a non-critical activity between its earliest start time and latest allowable time, project manager may be able to lower the maximum resource requirements. The following two general rules are normally used in scheduling non-critical activities.

1. If the total float of a non-critical activity is equal to its free float, then it can he schedule any where between its earliest start and latest completion times.

2. If the total float is a non-critical activity is more than its free float, then its starting time can be delayed relative to its earliest start time by no more than the amount of its free float without affecting the scheduling of its immediately succeeding activities.