System Engineering 3(3+0)

LESSON 3. Time cost Optimization- Problems

Examples

The following table gives data on normal time, and cost and crash time and cost for a project.

Activity	Normal		Crash
	Time (Weeks)	Cost (Rs)	Time (Weeks)	Cost (Rs)
1-2	3	300	2	400
2-3	3	30	3	30
2-4	7	420	5	580
2-5	9	720	7	810
3-5	5	250	4	300
4-5	0	0	0	0
5-6	6	320	4	410
6-7	4	400	3	470
6-8	13	780	10	900
7-8	10	1000	9	1200

Indirect cost is Rs 50 per week

(a)  Draw the network and identify the critical path with double line.

(b) What are the normal project duration and associated cost?

(c)  Find out the total float associated with each activity.

(d) Crash the relevant activities systematically and determine the optimal project completion time and cost

Solution:

(a)  The network for normal activity times indicates a project completion time of 32 weeks with the critical path: 1 – 2 – 5 – 6 – 7 – 8, as shown in Fig. 24.

Fig. 24   Network Diagram

(b) Normal project duration is 32 weeks and the associated cost is as follows:

Total cost = Direct normal cost + Indirect cost for 32 weeks

                 = 4,220 + 50 x 32 = Rs 5,820

(c)  Calculations for total float associated with each activity are shown in Table 10

Table 10

Activity	Total Float (Li – Ei) – tij
1 - 2	(3 – 0) – 3 = 0
2 – 3	(7 – 3) – 7 = 1
2 – 4	(12 – 3) – 7 = 2
2 – 5	(12 – 3) – 9 = 0
3 – 5	(12 – 6) – 5 = 1
4 – 5	(12 – 10) – 0 = 2
5 – 6	(18 – 12) – 6 = 0
6 – 7	(22 – 18) – 4 = 0
6 – 8	(32 – 18) – 13 = 1
7 – 8	(32 – 22) – 10 = 0

 

(d) For Critical activities, crash cost-slope is given in Table 11. The minimum value of crash cost per week is for activity 2-5 and 5-6. Hence, Crashing activity 2-5 by 2 days from 9 weeks to 7 weeks. But the time should be reduced by 1 week only otherwise another path 1-2-3-5-6-7-8 becomes a paralled path. Network as shown Fig. 25 is developed when it is observed that new project time is 31 weeks and the critical paths are 1 – 2 – 5 – 6 – 7 – 8 and 1 – 2 – 3 – 5 – 6 – 7 – 8.

Table 11

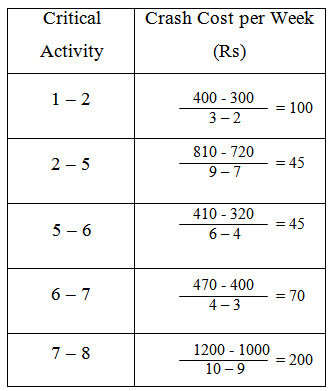
Fig. 25   Network Diagram

With crashing of activity 2 – 5, the new total cost involved can be calculated as follows:

New total cost = Total direct normal + Increased direct cost due to crashing of activity

                       (2 – 5 ) + indirect cost for 31 weeks

                   = (4,220 + 1 x 45) + 31 x 50 = 4,265 + 1,550 = Rs 5,815

Now with respect to network given in Fig. 25, the new possibilities for crashing in the critical paths are listed in Table 12.

Table 12

Critical Activity	Crashed Cost per Week (Rs)
1 – 2	100
2 – 5	x (Crashed)
2 – 3	0 (No crashing is needed)
3 – 5	50
5 – 6	45
6 – 7	70
7 – 8	200

 

The minimum value of crashed cost slope is for activity 5 – 6. Hence, crashing it by 2 weeks from 6 weeks to 4 weeks. The new network diagram will now look like as show in Fig. 26

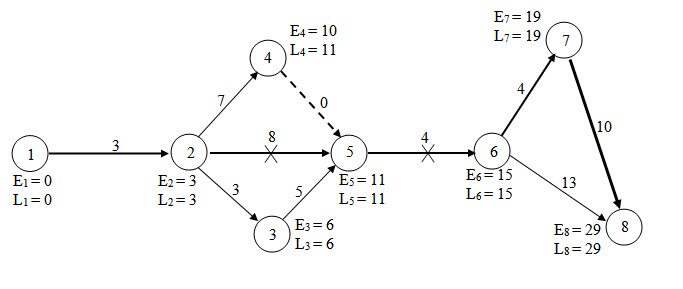
Fig. 26   Network Diagram

It may be noted in Fig.26, that both critical paths shown in Fig.25 remain unchanged because activity 5 – 6 is common between critical paths shown in Fig. 25. But with this crashing of activity 5 – 6 by 2 weeks, the new cost involved is:

New total cost = Total direct normal + Increased direct cost due to crashing of

                       5 – 6 + indirect cost for 29 weeks

                   = (4,220 + 1 x 45 + 2 x 45) = 29 x 50 = Rs 5805

With respect to network given in Fig 26, the new possibilities for crashing in the critical paths are listed in Table 13.

Table 13

Critical Activity	Crashed Cost per Week (Rs)
1 – 2	100
2 – 3	0 (No crashing is needed
2 – 5	x (Crashed))
5 – 6	x (Crashed)
6 – 7	70
7 – 8	200

 

The further crashing of 6 – 7 activity time from 4 weeks to 3 weeks will result in increased direct cost than the gain due to reduction in project time. Hence, here we must stop further crashing. The optimal project duration is 29 weeks with associated cost of Rs 5,805 as shown in Table 14.

Table 14 Crashing Schedule of the Project

Project Duration (Weeks)	Crashing Activity and Weeks	Direct Cost (Rs)			Indirect cost (Rs)	Total Cost (Rs)
		Normal	Crashing	Total
32	--	4,220	--	4,220	32 x 50 = 1,600	5,820
31	2 – 5(1)	4,220	1 x 45 = 45	4,265	31 x 50 = 1,550	5,815
29	5 – 6(2)	4,220	45 + 2 x 45 = 135	4,355	29 x 50 = 1,450	5,805
28	6 – 7(1)	4,220	135 + 1 x 70 = 205	4,425	28 x 50 = 1,400	5,825