Soil Mechanics 3(2+1)

LESSON 19. Seepage in Soil

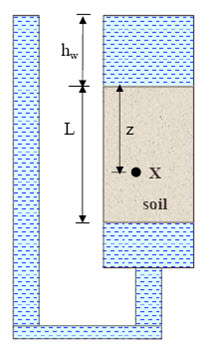
Fig. 19.1. Stresses within the soil under static condition.

Figure 19.2 shows the stresses within soil due to downward flow of the water. The total vertical stress (σ_v) at a point X within the soil is:

σv = \[\gamma\]_wh_w +   \[\gamma\]_satz                 (19.4)

The pore water pressure at point A is: u_A = \[\gamma\]_w h_w          (19.5)

The pore water pressure at point B is: u_B = \[\gamma\]_w (h_w +L-h_L)               (19.6)

Thus, the pore water pressure at point X is:

u = \[\gamma\]_w h_w + \[\gamma\]_w(L-h_L)(z/L) = \[\gamma\]_w h_w + _\[\gamma\]w(z-iz) = \[\gamma\]_w (h_w+z) - \[\gamma\]_w iz             (19.7)

Thus, effective stress is: σ_v' = σ_v – u = \[\gamma\]^' z + \[\gamma\]_wiz                                     (19.8)

where i is the hydraulic gradient. \[\gamma\]_wiz is the amount of reduction in pore water pressure and amount of increment in effective stress due to downward  water flow. 

Figure 19.3 shows the stresses within soil due to upward flow of the water.

The total vertical stress (σ_v) at appoint X with the soil is: σ_v = \[\gamma\]_wh_w + \[\gamma\]_satz          (19.9)

The pore water pressure at point A is: u_A = \[\gamma\]_w h_w                                           (19.10)

The pore water pressure at point B is: u_B = \[\gamma\]_w (h_w +L+h_L)                              (19.11)

Thus, The pore water pressure at point X is:

u = \[\gamma\]_w h_w + \[\gamma\]_w(L+ h_L)(z/L) = \[\gamma\]_w h_w + \[\gamma\]_w(z+iz) = \[\gamma\]_w (h_w+z) + \[\gamma\]_wiz                (19.12)

Thus, effective stress is: σv'= σ_v – u = \[\gamma\]^' z - \[\gamma\]g_wiz                                    (19.13)

where i is the hydraulic gradient. \[\gamma\]_wiz is the amount of increment in pore water pressure and amount of reduction in effective stress due to upward water flow.

Eq. (19.13) can be written as:  

\[{\sigma '_v}={\gamma _w}z\left({{{\gamma '} \over {{\gamma _w}}} - i} \right)\]              (19.14)

In Eq. (19.14), \[\gamma\]'/ \[\gamma\] is called “Critical Hydraulic Gradient (i_c). If i > i_c, the effective stresses become negative. Thus, there is no inter granular contact between the soil grains and failure takes place. This is called “Quick Condition” for granular soil.

Fig. 19.2. Stresses within the soil due to downward water flow.

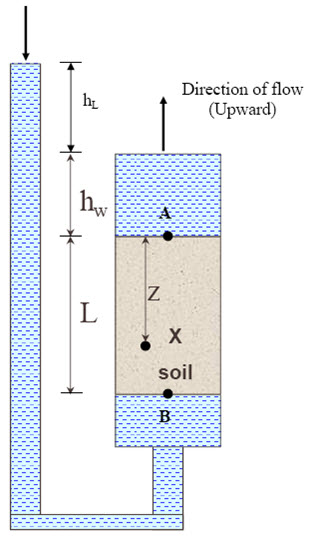
Fig.19.3. Stresses within the soil due to upward water flow.

19.2 Laplace’s Equation

This equation is valid for two-dimensional flow when soil mass is fully saturated and Darcy’s law is valid. The soil mass is homogeneous and isotropic, soil grains and pore fluid are assumed to be incompressible. Flow condition does not change with time i.e. steady state condition exists. The equation can be written as (under the assumed conditions):

\[{{{\partial ^2}h} \over {\partial {x^2}}} + {{{\partial ^2}h} \over {\partial {z^2}}}=0\]               (19.15)

where h is the head loss in x and z direction. The solution of Laplace equation gives two sets of curves perpendicular to each other. One set is known as flow lines and other set is known as equipotential lines. The flow lines indicate the direction of flow and equipotential lines are the lines joining the points with same total potential or elevation head.

 

References

Ranjan, G. and Rao, A.S.R. (2000). Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

PPT of Professor N. Sivakugan, JCU, Australia.

 

Suggested Readings

Ranjan, G. and Rao, A.S.R. (2000) Basic and Applied Soil Mechanics. New Age International Publisher, New Delhi, India.

Arora, K.R. (2003) Soil Mechanics and Foundation Engineering. Standard Publishers Distributors, New Delhi, India.

Murthy V.N.S (1996) A Text Book of Soil Mechanics and Foundation Engineering, UBS Publishers’ Distributors Ltd. New Delhi, India.

PPT of Professor N. Sivakugan, JCU, Australia (www.geoengineer.org/files/permy-Sivakugan.pps‎).