Strength of Material 3(2+1)

LESSON 26. Rivet Joints: Design

26.1.1 Tearing of plate

 

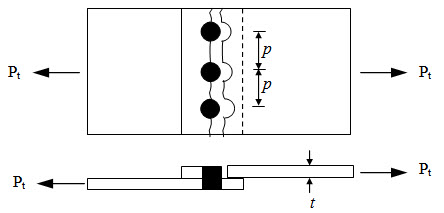
Fig. 26.1.

 The maximum allowable force P_t can be determined as,

\[{P_t}={\sigma _t}\left( {b - nd} \right)t\]

where,

\[{\sigma _t}={\rm{ allowable tensile stress of the plate material}}\]

\[b={\rm{ width of the plate}}\]

\[n={\rm{ number of rivets in the row where tearing takes place}}\]

\[d={\rm{ Diameter of the hole}}\]

26.1.2 Shearing of rivet

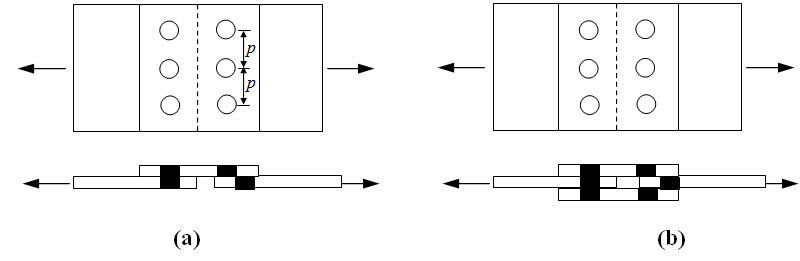
Fig. 26.2.

The maximum allowable force P_s can be determined as,

\[{P_s}=n{\sigma _s}\left({{\pi\over 4}{d^2}} \right)\]  for lap joints / single cover butt joints (Figure 26.2a)

\[{P_s}=2n{\sigma _s}\left({{\pi\over 4}{d^2}}\right)\]  for double cover butt joints (Figure 26.2b)

where,

\[{\sigma _s}={\rm{ allowable shear stress of the rivet material}}\]

\[n={\rm{ number of rivets in the row where tearing takes place}}\]

\[d={\rm{ Diameter of the hole}}\]

26.1.3 Crushing/ Bearing of rivet

The maximum allowable force P_b can be determined as,

\[{P_b}=n{\sigma _b}dt\]

where,

\[{\sigma _b}={\rm{ allowable bearing stress between rivet and the plate material}}\]

\[n={\rm{ number of rivets in the row where tearing takes place}}\]

\[d={\rm{ Diameter of the hole}}\]

Design strength of a riveted joint = min (P_t,P_s,P_b)

A multiple riveted joint may fail either in a single or a combination of above three mechanisms. In such cases all possible combination has to be considered in order to determine the design strength of the joint.

26.2 Unwin’s Formula                                                     

Unwin’s formula gives a relation between hole diameter of rivet and thickness of the connected plates. The Unwin’s formula is,

When t > 8mm,  \[d=6\sqrt t\]

When t < 8mm the hole diameter is determined by equating bearing strength and shear strength of the joint as,

\[{\sigma _b}t={\pi\over 4}d{\sigma _s} \Rightarrow d={{4t} \over \pi }{{{\sigma _b}} \over {{\sigma _s}}}\]

In any case d should not be less the thickness (t) of the plate.

 

Example                                                                           

In a single riveted lap joint, the pitch of the rivet is 100mm, thickness of the plate is 15mm and rivet diameter is 30 mm. Allowable stresses are σ_t = 450 MPa , σ_s = 350MPa and σ_b = 600MPa. Determine the design strength of the joint per pitch length.

Tearing strength,

\[{P_t}={\sigma _t}\left( {b - nd} \right)t\]

Since strength is to be determined per pitch length, b = p and n = 1 . Therefore,

\[{P_t}={\sigma _t}\left({p - d} \right)t=450 \times\left({100-30}\right)\times 15=472.5{\rm{ kN}}\]

Shearing strength,

\[{P_s}={\sigma _s}\left({{\pi\over 4}{d^2}}\right)=350\times {\pi \over 4}\times{30^2}=247.28{\rm{ kN}}\]

Crushing / Bearing strength,

\[{P_b}={\sigma _b}dt = 600 \times 30 \times 15=270{\rm{ kN}}\]

Design strength = min (P_t,P_s,P_b) = 147.2 kN.

Efficiency of the joint \[{\rm{Efficiency }}(\eta )={{{\rm{strength of joint}}} \over {{\sigma _t}pt}}={{{\rm{247}}{\rm{.28}} \times {\rm{1000}}} \over {450 \times 100 \times 15}}=36.63\% \]

 

Suggested Readings

Subramanian, N. (2008). Design of Steel Structures. Oxford University Press. 

Duggal, S.K. (2010). Limit State Design of Steel Structures. First Edition, Tata McGraw - Hill Education.