Strength of Material 3(2+1)

LESSON 28. Welded Joints: Design

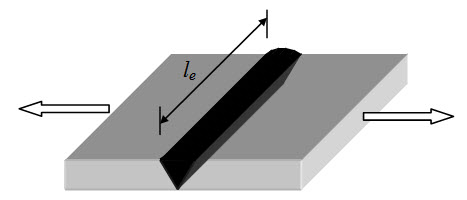
Fig.28.1.

The design strength of butt joint in tension is,

\[{T_d}={\sigma _t}{l_e}{t_e}\]

where,

\[{t_e}={\rm{effective throat dimension of the weld}}\]

\[{l_e}={\rm{effective length of the weld}}\]

28.1.2 Fillet Joints

Fillet joints generally fail in shear.

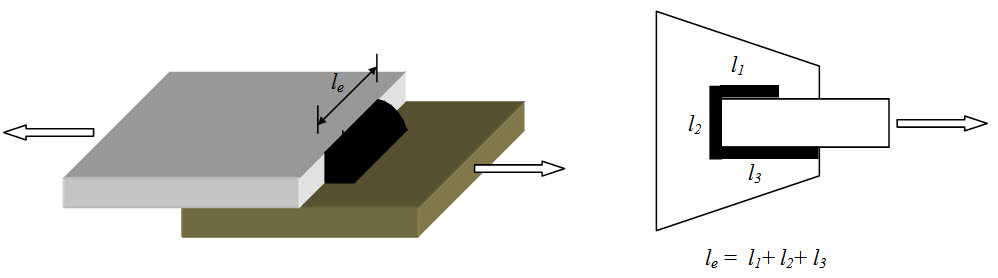
Fig. 28.2.

The design strength of fillet joint in shear is,

\[{V_d}={\sigma _S}{l_e}{t_e}\]

where,

\[{\sigma _S}={\rm{ allowable shear stress of the weld}}\]

\[{t_e}={\rm{effective throat dimension of the weld}}\]

\[{l_e}={\rm{effective length of the weld}}\]

28.1.3 Circular fillet weld subjected to torsion

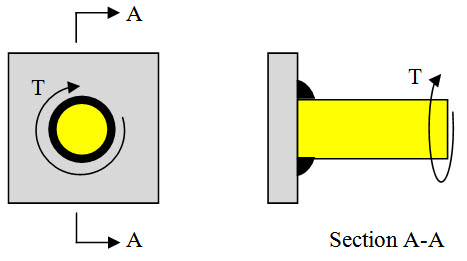
Fig. 28.3.

Maximum shear stress occurs at the throat area and is given by,

\[{\tau _{\max }}={{T\left( {0.5d + {t_e}} \right)} \over J}\]

where,

\[d={\rm{outer diameter of the shaft }}\]

\[J={\rm{polar moment of area of the throat section}}={\pi\over {32}}\left[ {{{\left( {d + 2{t_e}} \right)}^4} - {d^4}} \right]\]

Now the maximum shear stress \[{\tau _{\max }}\]  should not be more than the allowable shear stress of the weld. Therefore at the limiting case,

\[{\sigma _s}={\tau _{\max }}={{T\left( {0.5d + {t_e}} \right)} \over J}\]

 

Example 1

Find the length of the fillet weld required for the following connection. Both plates are 10mm thick. Assume allowable shear stress of the weld is 70MPa.

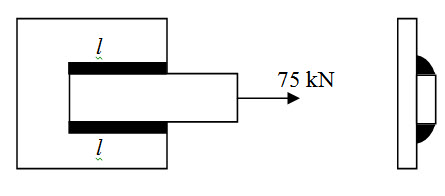
Solution

Effective length of the fillet weld \[{l_e}=2l\]

Effective throat dimension \[{t_e}={t \over {\sqrt 2 }}\]              [ t is the thickness of the plate]

Therefore, design strength of the weld,

\[{V_d}={\sigma _S}{l_e}{t_e}=70 \times {10^6} \times 2l \times {{10 \times {{10}^{ - 3}}} \over {\sqrt 2 }}=19.8 \times {10^5}l\]

Equating V_d  with the applied load,

\[19.8 \times {10^5}l = 75 \times {10^3} \Rightarrow 37.87{\rm{ mm}}\]

 

Example 2

Two plates of thickness 16mm and 12mm are to be connected by a groove weld. The joint is subjected to a tensile load of 300kN. Assume allowable tensile stress of the weld is 250MPa. Determine the length of the weld required for the following cases.

(i) Single V groove joint (Figure 28.5a)

(ii) Double V groove joint (Figure 28.5b)

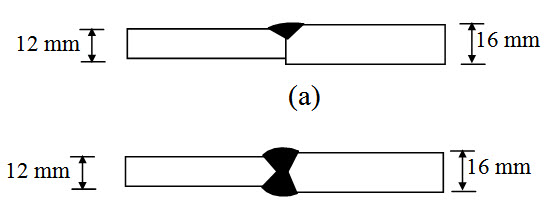
Fig. 28.5.

Solution

(i) case 1

Effective throat dimension \[{t_e}={5 \over 8} \times {\rm{thickness of thinner plate}}={5 \over 8} \times {\rm{12}}=7.5{\rm{ mm}}\]

\[{T_d}={\sigma _t}{l_e}{t_e}\]

\[\Rightarrow 300 \times {10^3} = 250 \times {10^6} \times {l_e} \times 7.5 \times {10^{ - 3}}\]

\[\Rightarrow {l_e}=160{\rm{ mm}}\]

(ii) case 2

Effective throat dimension \[{t_e}={\rm{thickness of thinner plate}}=12{\rm{ mm}}\]

\[{T_d}={\sigma _t}{l_e}{t_e}\]

\[\Rightarrow 300 \times {10^3}=250 \times {10^6} \times {l_e} \times 12 \times {10^{ - 3}}\]

\[\Rightarrow {l_e} = 100{\rm{ mm}}\]

 

 

Suggested Readings

Subramanian, N. (2008). Design of Steel Structures. Oxford University Press. 

Duggal, S.K. (2010). Limit State Design of Steel Structures. First Edition, Tata McGraw - Hill Education.