Strength of Material 3(2+1)

LESSON 30. Stability Analysis of Gravity Dams: Stability

Fig. 30.1.

where,

W = Self weight of the gravity dam. It acts at a distance x₁  from the  vertical line passing through the toe of the dam.

F_V = Weight of water on the inclined part of the upstream face. It acts at a distance x₂  from the  vertical line passing through the toe of the dam.

F_H = \[{1 \over 2}{\gamma _w}h_u^2\] = horizontal water pressure on upstream face. It acts at a distance y from the base of the dam.

U =  \[{1 \over 2}{\gamma _w}\left( {{h_d} + {h_u}} \right)b\]  Uplift force. It acts at a distance x₃  from the  vertical line passing through the toe of the dam.

R = Resultant of W, F_V, F_H  and U. R_x and R_y are the components of R.

Force due to horizontal water pressure (F_H) and uplift pressure (U) will cause overturning moment about the toe of the dam. This overturning moment will be stabilized mostly by the self weight of the dam W. Weight of water on the inclined part of the upstream face F_V will also produce some stabilizing moment. A gravity dam is considered to be safe against overturning if the stabilizing moment is higher than the overturning moment. The factor of safety against overturning is defined as,

\[FOS{\rm{ against overturning }}={\rm{ }}{{{\rm{Total stabilizing moment}}} \over {{\rm{Total overturning moment}}}}\]

The horizontal force acting on the dam is balanced either by friction alone or by friction and shear strength of the joint. A dam will fail in sliding at its base, or at any other level, if the net horizontal force causing sliding is more than the resistance available at that level. The factor of safety against sliding is defined as,

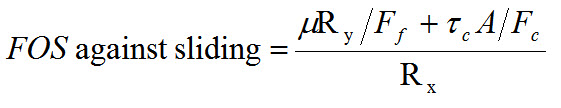
Where,

μ = Coefficient of friction

t_c = Permissible cohesion/ shear stress

A = cross-sectional area

F_f = partial safety factor in friction (Table 1 in IS:6512 – 1984)

F_c = partial safety factor in cohesion/shear (Table 1 in IS:6512 – 1984)

 

Suggested Readings

Garg, S.K. Irrigation Engineering and Hydraulic Structures. Khanna Pub.