Engineering Mechanics 3(2+1)

LESSON 19.

Types of beams: A beam is a structural member subjected to a system of external forces at right angles to its axis.

(i) Cantilever beam: If such a member is fixed or built in at one end while its other end is free, the member is called a cantilever. Fig.19.1

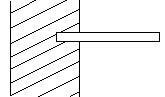
Fig.19.1

(ii) Simply or Freely Supported Beam: If the ends of a beam are made to freely rest on supports then the beam is called freely or simply supported beam. Fig.19.2

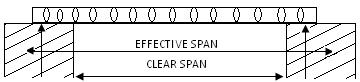
Fig.19.2

(iii) Fixed Beam: If the beam is fixed at both its ends, it is called a built-in or fixed beam. Fig.19.3.

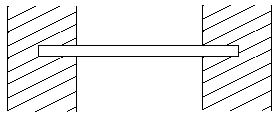
Fig.19.3

(iv) Continuous Beam: A beam which is provided with more than two supports is called a continuous beam. Fig.19.4.

Fig.19.4

Types of Loads: Beams may be subjected to various types of loads.

• Concentrated or Point Load: It is a load applied over a small area.
• 

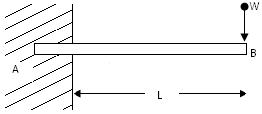
Fig.19.5

• Uniformly Distributed Load: It is a load which is spread on some length of a beam. It is expressed by its intensity (Newton/meter). if the intensity of the distributed load is constant the load is called uniformly distributed load.

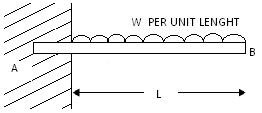
Fig.19.6

• Uniformly Varying Load: It has an intensity that varies according to some law along the length of the beam.

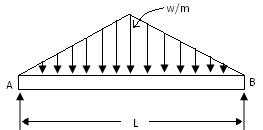
Fig.19.7

• Gradually Varied Load:

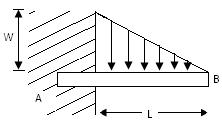
Fig.19.8

19.2 STRESS

The force of resistance offered by the body against the deformation is called the stress. The external force acting on the body is called the load. In other words,

• Under the influence of two equal and opposite forces P, the body in Fig.19.9 is in equilibrium. It deforms (stretches), and the stress (tensile) is developed.

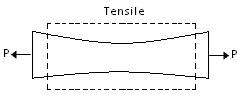
Fig.19.9

• Under the influence of two equal and opposite moments M, the body in Fig.19.10 deforms (bends in this case), and the stress (bending) is developed.

Fig.19.10

• A single force or a moment does not put the body under any stress. For a body to be under any stress, two equal and opposite forces or moments are necessary.

Mathematically Stress is written as

σ = \[{P \over A}\]

where σ = Stress

P = External force or Load

A = Cross-sectional area

The SI units of the stress is N/m².

19.3 STRAIN

When a body is subjected to some external force, there is some change of dimensions of the body. The ratio of change of dimension of the body to the original dimension is known as Strain.

Strain (e) = \[{{Changeinlength} \over {Originallength}}\]

Strain is unit less.

19.4 TYPES OS STRESSES

The important types of simple stresses are:

(i) Tensile Stress

(ii) Compressive Stress

(iii) Shear Stress

(i) Tensile Stress: The stress induced in a body, when subjected to two equal and opposite pulls as shown in Fig.19.11 as a result of which , there is an increase in length, is known as tensile stress.

The ration of increase in length to the original length is known as tensile strain.

\

Fig.19.11

Let P = force acting on the body

       A = Cross-sectional area of the body

       L = Original length of the body

     dL = increase in length due to pull P acting on the body

      σ = stress induced in the body

      e = strain

Tensile stress (σ) = \[{P \over A}\]

and Tensile strain (e) = \[{{increaseinlength} \over {Originallength}}\]   =  \[{dL \over L}\]

(ii) Compressive Stress: The stress induced in a body, when subjected to two equal and opposite pushes as shown in Fig.19.12 as a result of which there is decrease in length of the body, is known as compressive stress.

The ratio of decrease in length to the original length is known as compressive strain.

Fig.19.12

 

Compressive Stress (σ) = \[{P \over A}\]

Compressive Strain (e) = \[{{decreaseinlength} \over {Originallength}}\]  = \[{dL \over L}\]

(iii) Shear Stress: The stress induced in a body, when subjected to two equal and opposite forces which are acting tangentially across the resisting section as a result of which the body tends to shear off across the section, is known as shear stress.

The corresponding strain is known as shear strain.

Fig.19.13 shows a rectangular block of height l and length L and width unity.

Fig.19.13

Let the bottom face of the block be fixed to a surface EF. Let a force P be applied tangentially along the top face of the block. Such a force acting tangentially along a surface is called a shear force.

For the equilibrium of the block, the surface EF will offer a tangential reaction P equal and opposite to the applied tangential force P. Let the block be taken to consist of two parts G and H to which it is divided by a section XX. Consider the equilibrium of the part G in Fig.19.14

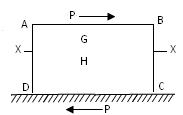
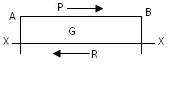
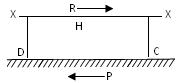
Fig.19.14

In order the part G may not move from left to right, the part H will offer a resistance R along the section XX such that R = P.

Similarly, considering the equilibrium of the part H, we find that the part G will offer a resistance R along the section XX such that the resistance R along the section XX is called a shear resistance.

Fig.19.15 shows a failure at the section XX caused by the tangential forces acting on the top and bottom faces of the block. This type of failure is called a shear failure. In shear failure, the two parts into which the block is separated, slide over each other. Hence if such a shear failure should not occur, the section XX must be able to offer tangential resistances along the section opposing the force P at the top face and the force P at the bottom face. For the equilibrium of the system of the shear resistance R should be equal to the tangential load P. Therefore, R = P

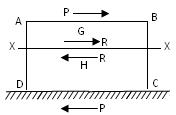
Fig.19.15

The intensity of the shear resistance along the section XX is called the shear stress.

Shear Stress = q = \[{R \over P}\] = \[{{Shear resistance} \over {Shear Area}}\]  = \[{R \over {L \times 1}}\]

Fig.19.16(a) shows a rectangular block subjected to shear forces P on its top and bottom faces.

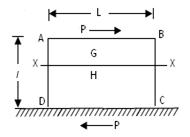
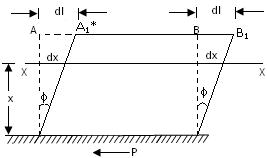
                        Fig.19.16

When the block does not fail in shear, a shear deformation occurs as shown in Fig.19.16(b). If the bottom face of the block be fixed, it can be realized that the block has deformed to the position A₁B₁CD.

Let us now imagine that the block consists of a number of horizontal layers. These horizontal layers have undergone horizontal displacements by different amounts with respect of the bottom face. We can assume that the horizontal displacement of any horizontal layer is proportional to its distance from the lower face of the block.

Let the horizontal displacement of the upper face of the block be dl. Let the height of the block be l.

The ratio \[{{dl} \over l}\]  =  \[{{Transversedisplacement} \over {Distancefromthelowerface}}\] is called shear strain.

19.5 ELASTIC LIMIT

When an external force acts on a body, the body tends to undergo some deformation. If the external force is removed and the body comes back to its original shape and size, the body is known as elastic body.

• The body will regain its previous shape and size only when the deformation caused by the external force, is within a certain limit. Thus there is a limiting value of force upto and within which the deformation completely disappears on the removal of forces. The value of stress corresponding to this limiting force is known as the elastic limit.

 

Hook’s Law: It is observed that when a material is loaded such that the intensity of stress is within a certain limit, the ratio of the intensity of stress to the corresponding strain is constant which is a characteristic of that material.

\[{{Intensityofstress} \over {Strain}}=constant\]

In the case of axial loading, the ration of the intensity of tensile or compressive stress to the corresponding strain is constant and is called Modulus of Elasticity or young’s Modulus.

It is denoted by E.

E = \[{\sigma\over e}\]