Farm Power & Machinery Management 3(2+1)

Lesson 9. Power Requirements

i.e.

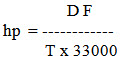
Where,

hp        = horse power

D         = distance travelled in ft

F          = force exerted in lb

T          = time taken in min

It can also be written as

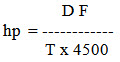
Where,

hp        = horse power

D         = distance travelled in m

F          = force exerted in kg_f

T          = time taken in min

It can be further written as

Lesson 9 : Solved examples

Example 1 : An implement requires 300 kg force to pull it through a distance of 100 m in 5 min. Find the power required to pull the implement.

Solution:

Given        F = 300 kg_f

D = 100 m

T = 5 min

So       

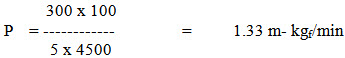
Example 2 : A tractor pulls a draught load of 1000 kg while travelling at a speed of 60 m/min. Find the horse power (hp) developed by the tractor.

Solution:

Drawbar Power: Power requirement of a tractor at its drawbar can also be estimated by the following formulae:

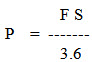
Where,

P  = drawbar power, kW

F  = draught, kN

S  = speed, km/h

Or,

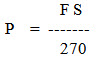
Where,

P  = drawbar power, hp

F  = draught, kg_f

S  = speed, km/h

Power requirement for some of the implements is given in Table 3.1. The drawbar power output is always less than Power-Take-Off (PTO) power output because of drive wheel slippage, tractor rolling resistance and friction losses in the drive train between the engine and the wheels. The sum of these losses may be represented by a tractive & transmission (T&T) coefficient. The tractive & transmission coefficient is defined as

T&T coefficients for four-wheel drive tractors are somewhat higher than those for two wheels drive tractors.  Track type tractors seldom have more than 5% slips even on soft soil. The value of tractive and transmission coefficient for track type tractors varies between 0.80 and 0.85 on firm soil and 0.70 and 0.75 on soft soil. The PTO power corresponding to drawbar power is determined by applying an appropriate T&T coefficient.

Rotary power: It is defined as

 

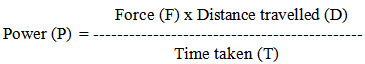
Example: If a belt produces a tangential force of 1000 N on a pulley having radius of 0.30 m at a speed of 200 rpm, the power it will be

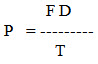
Given F = 1000 N                 

          D = distance covered = 2 p r x rpm

              = 2 \[\pi \] x 0.30 x 200 m/min

          T = 1 min

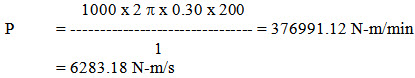
1 W     = 1 N-m/s

P          = 6283.18 W               =          6.28 kW

Fluid power: It is defined as the product of a weight rate of flow and the resistance to that flow called the head of the flow. Head describes the height of a column of fluid whose mass creates at the bottom a pressure equivalent to that in the flowing system. Thus,

Example: If 100 kg of water is to be pumped to the height of 30 m in 100 s, the power required would be

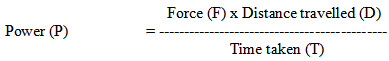
Given        F = 100 kg       = 100 x 9.8 N  = 980 N

                      D = 30 m

                      T = 100 s

So

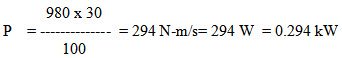
The pressure of the fluid and not its head is used in most calculations and expressed in Pascal (Pa).

1 Pa     = 1 N/m²

1 kPa   = 1000 Pa        = 0.145 psi

1 MPa = 1000 kPa

1 bar    = 100 kPa        = 1 atm

Hydraulic power (Ph): It is expressed as

       

Where,

p          = gauge pressure, k Pa

Q         = flow rate, l/s

C         = constant, 1000

It can also be expressed as

      Ph        = 0.01667 Q Dp, kW

Where,

Q         = fluid flow rate, l/min

Dp       = pressure change, M Pa

Power-Take-Off (PTO) power: It is expressed as

Where,

P          = PTO power, kW

F          = tangential force, kN

R         = radius of force rotation, m

N         = revolutions per minute, rpm

T          = torque, N-m = F R