Site pages
Current course
Participants
General
Module- 1 Engineering Properties of Biological Mat...
Module- 2 Physical Properties of Biomaterials
Module- 3 Engineering Properties
Module- 4 Rheological Properties of Biomaterials
Module- 5 Food Quality
Module- 6 Food Sampling
Module- 7 Sensory quality
Module 8. Quality Control and Management
Module 9. Food Laws
Module 10. Standards and regulations in food quali...
Lesson 32. Sanitation in food industry
Lesson 9. Some basic concepts of rheologi
Application:
•Design / select equipment such as pumps, pipe lines, extruders, mixers, heat exchangers etc.
•Rheological behavior relates to food texture and sensory data
•To determine ingredient functionality in product development
•Shelf life testing
•To obtain some information about atomic and molecular scale phenomena
•To obtain constitutive relations
MECHANICALPROPERTIES are defined as those having to do with the behavior of the material under applied forces. Following this broad definition, such properties as stress strain behavior of a material under static and dynamic loading as well as flow characteristics of the material in air or in water, can be classified as mechanical properties
Rheology has been defined as" a science devoted to the study of deformation and flow. "Therefore, when the action of forces result in deformation and flow in the material, the mechanical properties will be referred-to as rheological properties. Moreover, rheology considers the time effect during the loading of a body.
Definition:
Rheology is the branch of science that deals with flow and deformation of materials under applied load.
Rheology also deals with the branch of mechanical properties where products have both solid and liquid like behavior.
Generally mechanical properties deal with deformation under applied load, whereas, rheology deals with both flow and deformation under applied stress.
Mechanical properties are intertwined with rheology when including strength properties.
Rheology: Group of physical properties that derive from the structure of the food.
Mohsenin (1986) defines mechanical properties as “those having to do with the behavior of the material under applied forces.” Rheology has been defined as “a science devoted to the study of deformation and flow,” or as “the study of those materials that govern the relationship between stress and strain.” “Stress” is defined as force components acting on a body per unit cross-sectional area or area of the deformed specimen (SI units in Pa). “Strain” is the change in size or shape (SI units in mm or percentage) of a body in response to the applied force (at a certain time or during continuous change as stress is applied). Rheologically, the behavior of a material is expressed in terms of stress, strain, and time effects. Therefore, properties that deal with the motion of the material as a result of an applied force can be included as mechanical forces.
There are three stresses that are commonly applied to characterize foods mechanically: compressive (directed toward the material), tensile (directed away from the material), and shearing (directed tangentially to the material). Shear stress is the most prevalent with fluids or viscous materials. Since strain is the response of the material to stress, compressive shear and tensile strains can be found. When small deformations are exerted under compression, foods can show a straight line in the stress strain plot, and its slope is called the “Young modulus of elasticity.” Rheologically, a material can deform in three ways: elastic, plastic, or viscous; it can be denoted by a spring friction element and a dashpot arranged in series or parallel, respectively, in rheological models.
Some basic terminologies in rheology:
Strain: the unit change , due to force, in the size or shape of a body referred to its original size or shape. Strain is non-dimensional quantity, but it is frequently expressed centimeter per centimeter, m/m, mm/mm etc.
Linear (tensile/ compressive ) strain: the change per unit length due to force in an original linear dimension
Axial strain: linear strain in a plane parallel to the longitudinal of the specimen.
Transverse strain: linear strain in a plane perpendicular to the axis of the specimen.
Shear strain (angular strain): the tangent of the angular change, due to force, between two lines originally perpendicular to each other through a point in a body.
Stress: the intensity of a point in a body of the internal forces or components of force that act on a given plane through the point. Stress is expressed in force per unit area (kg-force/ mm2)
Normal stress: The stress component perpendicular to a plane on which the forces act. Normal stress may be eitherTensile stress: it is the normal stress due to forces directed away from the plane on which they act.
- Tensile stress: it is the normal stress due to forces directed away from the plane on which they act.
2. Compressive stress: it is the normal stress due to forces directed toward the plane on which they act.
Shear stress: stress component tangential to the plane on which the forces act.
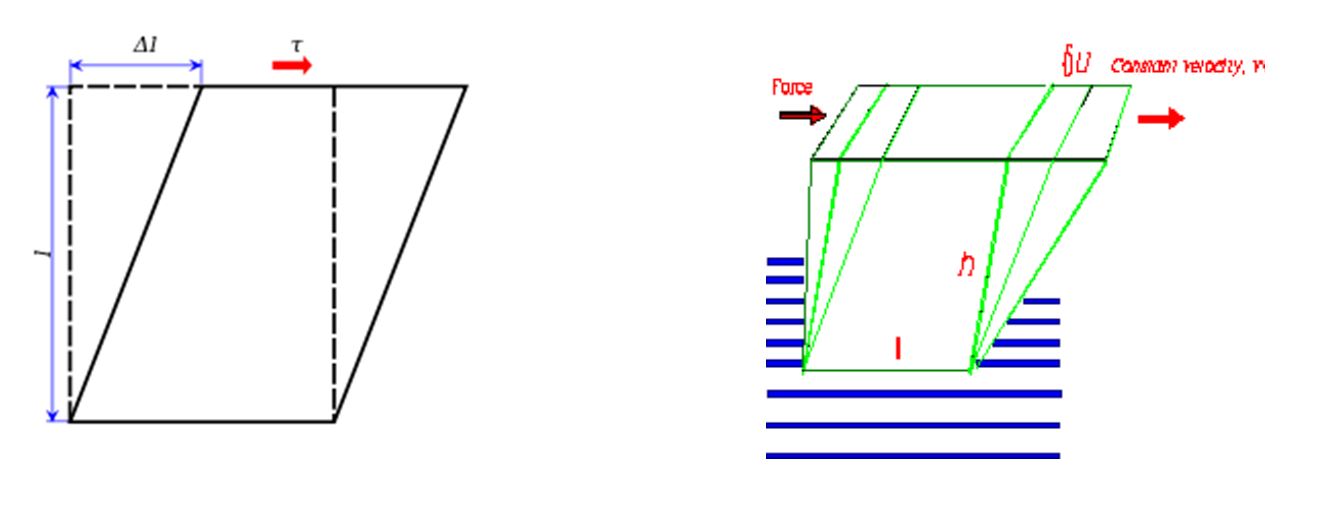
This type of deformation (lower fixed upper moving) is defined as a SHEAR DEFORMATION. The deformation δ u and h are used to define the:Shear Strain=δu/h The shear strain is simply a ratio of two lengths (displacement/gap) and so has no units. It is important since it enables us to quote pre-defined deformations without having to specify sizes of sample etc.
Shear Stress: The SHEAR STRESS is defined as F/A (A is the area of the upper surface of the cubel xw) Since the units of force are Newtons and the units of area are m2 it follows that the units of Shear Stress are N/M2 This is referred to as the PASCAL (i.e.1N/m2=1Pascal) and is denoted by the symbol σ. Shear Rate Consider the case of a cube of material that behaves as an ideal fluid. When we apply a shear stress (force) the material will continually deform at a constant rate as illustrated in figure.
The rate of change of strain is referred to as the SHEAR STRAIN RATE often abbreviated to SHEAR RATE and is found by the rate of change of strain as a function of time i.e. the differential SHEAR STRAIN /differential TIME.
Tensile strength: the maximum tensile stress that a material is capable of sustaining. Tensile strength is calculated from the maximum load during a tension test carried to rupture and the original cross sectional area of specimen.
Compressive strength: the maximum compressive stress that a material is capable of sustaining. Compressive strength is calculated from the maximum load during a compression test and the original cross sectional area of specimen
Strength: the resistance to applied force (kg/cm)
Ultimate strength: the stress corresponding to the rupture point (kg/cm2)
Bioyield strength: the stress corresponding to the bioyield point.
Pressure: a measure of the mean normal stress on a point of body (kg/cm2)
Deformation:
Deformation or distortion is the relative displacement of points within a body. Deformation like stress is a vector quantity. Ingeneral, deformation is accompanied either by change of volume or by change of shape. The change of shape is brought about by shear stresses. Material can be deformed by uniaxial compression, uniaxial tension, shear, and bulk compression:
Elastic limit: the greatest stress which a materials is capable of sustaining without any permanent strain remaining upon release of the stress.
Proportional limit: the greatest stress which a materials is capable of sustaining without any deviation from proportionality of stress to strain (Hooke’s law).
Yield point: the first stress in a material, less than the maximum attainable stress, at which an increase in strain occurs without an increase in stress.
Bioyield point: a point, as y on the stress-strain or force-deformation curve at which there occurs an increase in deformation with a decrease or no change of force. In some agricultural products, the presence of this bioyield point is an indicative of initial cell rupture in the cellular structure of the material. The bioyield point may occur at any point beyond the point LL, where the curve deviates from the initial straight line porti
A possible force-deformation curve for an agricultural product, LL: linear limit, y: yield point, R: rupture point
Rupture point: a point on the stress-strain or force-deformation curve at which the axially loaded specimen ruptures under a load. In biological materials, rupture may cause puncture of shell or skin, cracking or fracture planes. It may be stated that a “bioyield point” in these materials corresponds to a failure in the macrostructure of the specimen. In force deformation may occur at any point beyond the bioyield point. In a brittle material, rupture may occur in the early portion of the curve. In a tough material, rupture may take place after considerable plastic floe at such point as R.
Elasticity: the capacity of a material for taking elastic or recoverable deformation. In those portions of the curve before the point LL is reached, elongations are, in large part at least. Recoverable, and are a measure of elastic deformation.
Plasticity: the capacity of a material for taking plastic or permanent deformation. Since deformations from the bioyield point to the point of rupture are not all recoverable, the recoverable part can be taken as a measure of plastic deformation.
A possible force-deformation curve for an agricultural product, LL: linear limit, y: yield point, R: rupture point
Rupture point: a point on the stress-strain or force-deformation curve at which the axially loaded specimen ruptures under a load. In biological materials, rupture may cause puncture of shell or skin, cracking or fracture planes. It may be stated that a “bioyield point” in these materials corresponds to a failure in the macrostructure of the specimen. In force deformation may occur at any point beyond the bioyield point. In a brittle material, rupture may occur in the early portion of the curve. In a tough material, rupture may take place after considerable plastic floe at such point as R.
Elasticity: the capacity of a material for taking elastic or recoverable deformation. In those portions of the curve before the point LL is reached, elongations are, in large part at least. Recoverable, and are a measure of elastic deformation.
Plasticity: the capacity of a material for taking plastic or permanent deformation. Since deformations from the bioyield point to the point of rupture are not all recoverable, the recoverable part can be taken as a measure of plastic deformation.
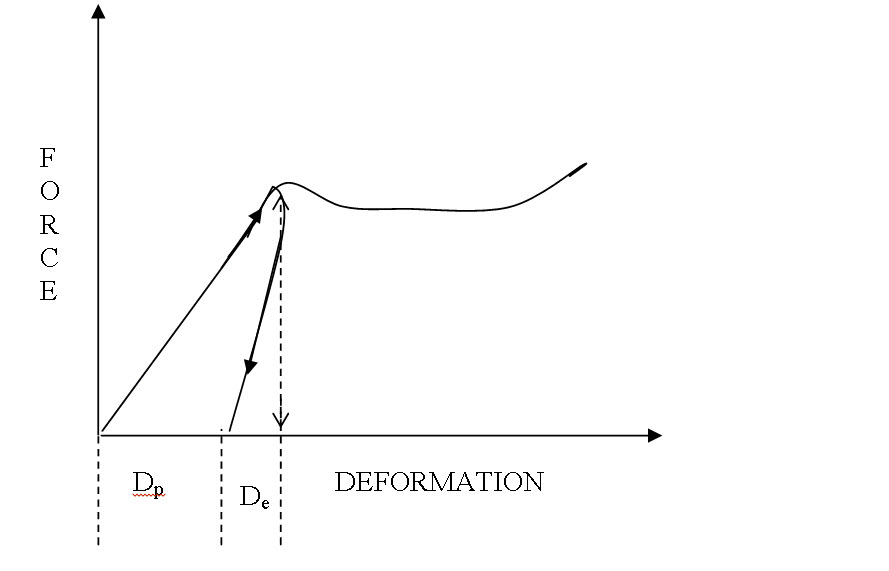
Degree of elasticity from a loading-unloading curve
Degree of elasticity: the ratio of elastic deformation to the sum of elastic and plastic deformation when a material is loaded to a certain load and then unloaded to zero load.
De= elastic or recoverable deformation
Dp= plastic or residual deformation
Degree of elasticity: De/ (De+Dp)
Toughness: the work required to cause rupture in the material. This can be approximated by the area under the stress-strain or force-deformation curve up to the point selected as the rupture point. If in estimating toughness, a force-deformation curve is uses, the size of the specimen and the loading surface area should be specified.
Resilience: the capacity of a material for storage of strain energy in the elastic range. Thus the area under the unloading curve is a measure of resilience of the material. As in the case of toughness, when a force-deformation curve is uses, the size of the specimen and the loading surface area should be specified.
Stiffness: stiffness or rigidity is indicated by the slope of the initial straight line portion of the curve. The ratio of stress to strain in this more or less elastic region of the curve may be referred to as the modulus of elasticity or “Young’s modulus”(kg/cm2)
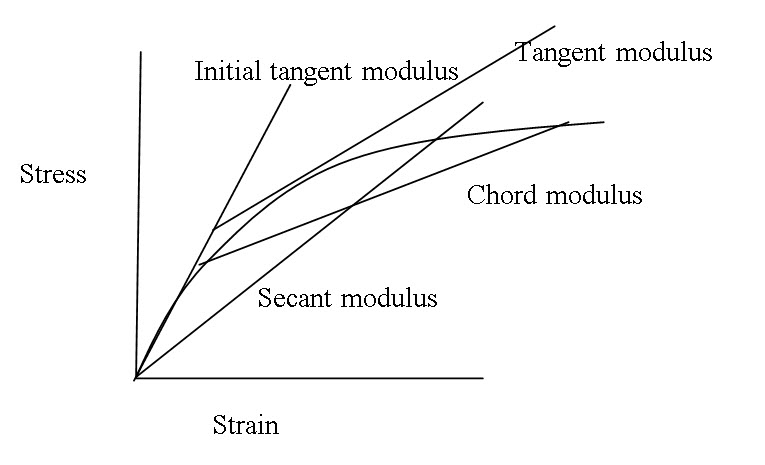
In the case of non-linear stress-strain behavior, stiffness or apparent modulus can be defined in terms of
Initial tangent modulus
Secant modulus
Tangent modulus
Chord modulus
Modulus of elasticity:
The ratio of stress to corresponding strain below the proportional limit
Initial tangent modulus: The slope of the stress-strain curve at the origin
Tangent modulus: The slope of the stress-strain curve at any specified stress or strain
Secant modulus: The slope of secant drawn from the origin to any specified point on stress – strain curve
Chord modulus: The slope of chord drawn between any two any specified point on stress – strain curve.
Poisons ratio: the absolute value of the ratio of transverse strain to the corresponding axial strain resulting from uniformly distributed axial stress below the proportional limit of the material.
 References:
References:
Mohsenin, N.N. 1986. Physical Properties of Plant and Animal Materials, 2nd ed.; Gordon and Breach Science Publishers: New York
Sahin S. & Sumnu, S. G. 2006. Physical Properties of Foods. Springer, USA