Fluid Mechanics 3(2+1)

Lesson-14: FLOW PATTERNS

14.1 Flow patterns

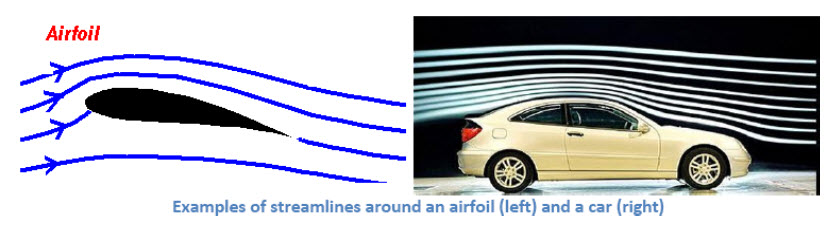
14.1.1 Streamlines

• In the study of fluid mechanics, streamlines are often drawn to visualize the flow field

• Streamline is a line that is everywhere tangent to the velocity vector at a given instant.

Consider an arc length

 

must be parallel to the local velocity vector

 

Geometric arguments results in the equation for a streamline

 

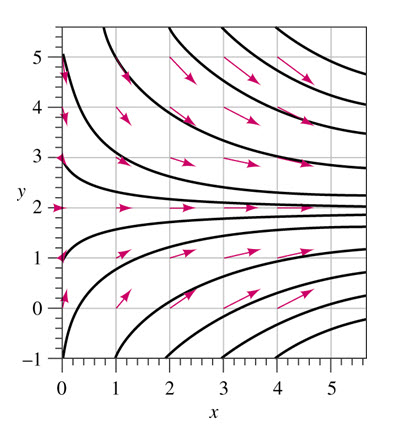
Stream Function

• Stream functions are for 2 dimensional flow only. In some fluid motion problems, this is a good enough approximation.  Also, typically stream functions are used for incompressible flow, although a slightly modified version can be used for steady state compressible fluid flows also.

• In any case, for from the continuity equation, for incompressible fluids, for 2 dimensional flow:

Consider x and y co-ordinates (assuming the flow is not there in z direction). Vx and Vy are related by the DE. Hence we seek a function which can represent both. (i.e. we want to see if we can replace two functions by one, since they are related).

Assume

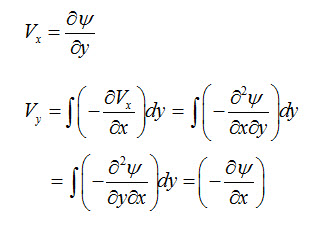
• Instead of two functions, V_x and V_y, we need to solve for only one function y - Stream Function

• Order of differential eqn increased by one

• The stream function is useful (a) as an aid in visualizing the fluid flow (b) as a mathematical tool in solving the fluid equations and obtaining the velocities, in some cases.

• The stream functions are the equations for stream lines. A fluid may not flow ‘across’ a streamline. It flows along the stream line. If a stream line’s stream function value is X and another stream line’s stream function value is Y, then the fluid flowing in the (imaginary) channel bounded by these two stream lines is given by X-Y (or Y-X, as appropriate!).

• Streamlines exist in 3D flow, but a corresponding stream function does not. (When we learn about velocity potentials, we can get an idea as to why). The stream lines in the 3D can be given by the equation:

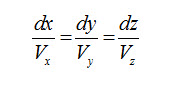14.2.2 Pathlines

• A pathline is the actual path traveled by a given fluid particle.

• The actual path that a single fluid particle takes is referred to as the pathline, i.e., it is the trajectory of a particular fluid particle. This is referred to as the Lagrangian viewpoint of the flow field. Experimentally, it can be achieved by tagging a fluid particle and tracing its motion throughout the flow field.

  

Particle location at time t:

 

Particle Image Velocimetry (PIV) is a modern experimental technique to measure velocity field over a plane in the flow field.

14.2.3 streakline

• A streakline is the locus of particles which have earlier passed through a particular point.

• A particular type of fluid-material line which is of much utility is the streakline, which is the locus of all particles which have passed a specified ("tagging") location in some interval of time.

• The use of dye, smoke or hydrogen bubbles to generate streaklines is a technique that is often used in experiments to visualize the flow field.

Streakline example: