Electrical Circuits 3(2+1)

LESSON 24. Functional and operational Transforms

(i) The unit step function \[f\left( t \right) = u\left( t \right)...................................................\left( {24.1} \right)\]

Where u(t)      = 1  for   t > 0

                       = 0 for    t < 0

\[L\left[ {\delta \left( t \right)}\right]=\int\limits_0^\infty{f\left(t \right){e^{-st}}\,\,dt}\]

\[\,\int\limits_0^\infty{1e-st\,\,dt={{e-st}\over {-s}}} l\nolimits_0^\infty={1\over s}\]

\[L\left[ {u\left( t \right)} \right]={1 \over s}...................................................\left( {24.2} \right)\]

(ii) Exponential function \[f\left( t \right)={e^{ - at}}\]

\[L\left({{e^{-at}}}\right)=\int_0^\infty{e - at.{e^{-st}}\,dt}\]

\[=\int_0^\infty{{e^{-\left({s+a}\right)t}}={{-1}\over{s+a}}\left[ {{e^{-\left({s + a}\right)t}}}\right]_0^\infty={1\over {s + a}}}\]

\[L\left[{{e^{-at}}}\right]={1\over{s + a}}...................................................\left( {24.3} \right)\]

(iii) The cosine function : cos wt  \[..................................................\left( {24.4} \right)\]

\[L\left( {\cos\,\omega t} \right)=\int\limits_0^\infty{\cos \,\omega t\,\,{e^{-st}}dt}\]

\[=\int\limits_0^\infty{{e^{-st}}\left[{{{{e^{j\omega t}}+{e^{-j\omega t}}}\over 2}}\right]}\,dt\]

\[={1 \over 2}\left[ {\int\limits_0^\infty{{e^{-\left({s-j\omega }\right)t}}dt+\int\limits_0^\infty{{e^{-\left({s + j\omega}\right)t}}dt}}}\right]\]

\[={1 \over 2}\left[{{{{e^{-\left({s-j\omega t}\right)t}}}\over{s-j\omega}}}\right]_0^\infty\,\, + \,{1\over 2}\left[{{{{e^{-\left({s+j\omega t} \right)t}}} \over {s + j\omega }}} \right]_0^\infty\]

\[={1 \over 2}\left[ {{1 \over {s - j\omega }}+{1\over {s + j\omega }}}\right]={s \over {{s^2} + {\omega ^2}}}\]

\[L\left( {\cos \,\,\omega t} \right)={s \over {{s^2} + {\omega ^2}}}...................................................\left( {24.5} \right)\]

(iv) The sine function : sin wt \[...................................................\left( {24.6} \right)\]

\[L\left( {\sin \,\omega t} \right)=\int\limits_0^\infty{\sin \,\omega t\,\,{e^{ - st}}dt}\]

\[=\int\limits_0^\infty{{e^{-st}}\left[ {{{{e^{j\omega t}}-{e^{-j\omega t}}}\over {2j}}} \right]} \,dt\]

\[={1 \over {2j}}\left[ {\int\limits_0^\infty{{e^{-\left({s-j\omega }\right)t}}dt-\int\limits_0^\infty{{e^{-\left({s+j\omega}\right)t}}dt}}}\right]\]

\[={1 \over {2j}}\left\{ {\left[ {{{{e^{ - \left( {s - j\omega t} \right)t}}} \over {s - j\omega }}} \right]_0^\infty \,\, + \left[ {{{{e^{ - \left( {s + j\omega t} \right)t}}} \over {s + j\omega }}} \right]_0^\infty } \right\}\]

\[={1\over {2j}}\left[ {{1\over {s - j\omega }} + {1 \over {s + j\omega }}} \right]={\omega\over {{s^2} + {\omega ^2}}}\]

\[L\left( {\sin \,\,\omega t} \right)={\omega\over {{s^2} + {\omega^2}}}...................................................\left( {24.7} \right)\]

(v) The function t”, where n is a positive integer

\[L\left( {t} \right)=\int\limits_0^\infty{t.{e^{ - st}}dt} ...................................................\left( {24.8} \right)\]

\[=\left[ {{{t{e^{-st}}} \over {-s}}}\right]_0^\infty-\int\limits_0^\infty{{{{e^{-st}}} \over {-s}}n{t^{n - 1}}dt}\]

\[={n \over s}\int\limits_0^\infty{{e^{-st}}\,t{n^{-1}}\,dt}\]

\[={n \over s}L\left( {{t^{n - 1}}} \right)...................................................\left( {24.9} \right)\]

        Similarly         \[L\left( {{t^{n - 1}}} \right)={{n - 1} \over s}L\left( {{t^{n - 2}}} \right)\]

By taking Laplace transformations of t^n-2, t^n-3 … and substituting in the above equation, we get

\[L\left( {t} \right)={n \over s}{{n - 1} \over s}{{n - 2} \over s}......{2 \over s}{1 \over s}L\left( {{t^{n - m}}} \right)\]

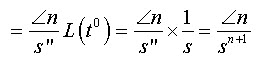
\[L\left( t \right)={1 \over {{s^2}}}...................................................\left( {24.10} \right)\]

(vi) The hyperbolic sine and cosine function

\[L\left( {\cosh \,\,at} \right)\,=\,\int\limits_0^\infty{\cosh \,at\,{e^{ - st}}dt} ...................................................\left( {24.11} \right)\]

\[=\int\limits_0^\infty{\left[ {{{{e^{at}}+{e^{-at}}}\over 2}}\right]}{e^{-st}}\,\,dt\]

\[={1 \over 2}\int\limits_0^\infty{{e^{-\left({s - a} \right)t}}\,dt + {1 \over 2}\int\limits_0^\infty{{e^{-\left({s + a} \right)t\,}}dt} }\]

\[={1 \over 2}{1 \over {s - a}} + {1 \over 2}{1 \over {s + a}}={s \over {{s^2} - {a^2}}}...................................................\left( {24.12} \right)\]

Similarly,

\[L\left( {\sinh \,at} \right)=\int\limits_0^\infty{\sinh \,\left( {at} \right){e^{ - st\,}}\,dt} ...................................................\left( {24.13} \right)\]

\[=\int\limits_0^\infty{\left[ {{{{e^{at}} - {e^{ - at}}} \over 2}} \right]} {e^{ - st}}\,\,dt\]

\[={1 \over 2}\int\limits_0^\infty{{e^{ - \left( {s - a} \right)t}}\,dt + {1 \over 2}\int\limits_0^\infty{{e^{ - \left( {s + a} \right)t\,}}dt} }\]

\[={1 \over 2}{1 \over {s - a}} + {1 \over 2}{1 \over {s + a}}={s \over {{s^2} - {a^2}}}...................................................\left( {24.14} \right)\]

Table 24.1 List of Laplace Transform Pairs

Type	\[f\left( t \right)\]	F(s)
Impulse	δ(t	1
Step	U(t)	\[{1 \over s}\]
ramp	t	\[{1 \over {{s^2}}}\]
exponential	e-at	\[{1 \over {s + a}}\]
sine	sin  ωt	\[{\omega\over {{s^2} + {\omega^2}}}\]
cosine	cos ωt	\[{s \over {{s^2} + {\omega^2}}}\]
Hyperbolic sine	sinh at	\[{a \over {{s^2} - {a^2}}}\]
Hyperbolic cosine	cosh at	\[{s \over {{s^2} - {a^2}}}\]
damped ramp	te-at	\[{1 \over {\left( {s + a} \right)}}\]
Damped sine	e-at sin ωt	\[{\omega\over{{{\left({s + a} \right)}^2} + {\omega^2}}}\]
Damped cosine	e-at cos ωt	\[{{s + a} \over {{{\left( {s + a} \right)}^2} + {\omega ^2}}}\]

 

24.2. Operational Transforms

Operational transforms indicate how mathematical operations performed on either  and F(s) are converted into the opposite domain.  The operations of primary interest are

(1) Multiplication by a constant

(2) Addition (subtraction)

(3) Differentiation

(4) Integration

(5) Translations in the time domain

(6) Translation in the frequency domain and

(7) Scale charging

Multiplication by Constant

From the defining integral, if

\[L\left[ {f\left( t \right)} \right]=F\left( s \right)\]

then \[L\left\{ {K\,f\left( t \right)} \right\}=K\,F\left( s \right)...................................................\left( {24.15} \right)\]

Consider a function \[f\left( t \right)\] multiplied by a constant K.

The Laplace transform of this function is given by

\[L\left[ {K\,f\left( t \right)} \right]=\int\limits_0^\infty{Kf\left( {t\,{e^{ - st}}\,dt} \right)} ...................................................\left( {24.16} \right)\]

\[=K\int\limits_0^\infty{f\left( t \right)\,{e^{ - st}}\,dt=LF\left( s \right)} ...................................................\left( {24.17} \right)\]

This property is called linearly property.

Addition (Subtraction)

Addition (subtraction) in the time domain translates into addition (subtraction) in the frequency domain.

This if

\[{f_1}\left( t \right)\buildrel L \over \longleftrightarrow {F_1}\left( s \right)\,and\]

\[{f_2}\left( t \right)\buildrel L \over \longleftrightarrow {F_2}\left( s \right),\,then\]

\[L\left[ {{f_1}\left( t \right) \pm {f_2}\left( t \right)} \right]={F_1}\left( s \right) \pm {F_2}\left( s \right)...................................................\left( {24.18} \right)\]

Consider two functions \[{f_1}\left( t \right)\] and \[{f_2}\left( t \right)\] . The Laplace transform of the sum or difference of these two functions is given by

\[L\left\{ {{f_1}\left( t \right) \pm {f_2}\left( t \right)} \right\}=\int\limits_0^\infty{\left\{ {{f_1}\left( t \right) \pm {f_2}\left( t \right)} \right\}{e^{ - st}}dt}\]

\[=\int\limits_0^\infty{{f_1}\left( t \right){e^{ - st}}dt \pm \int\limits_0^\infty{{f_2}\left( t \right){e^{ - st}}dt} }\]

\[={F_1}\left( s \right) \pm {F_2}\left( s \right)\]

\[L\left\{ {{f_1}\left( t \right) \pm {f_2}\left( t \right)} \right\}={F_1}\left( s \right) \pm {F_2}\left( s \right)...................................................\left( {24.19} \right)\]

The Laplace transform of the sum of the two or more functions is equal to the sum of transforms of the individual function.  This is called superposition property, if we can use of linearity and superposition properties jointly, we have

\[L\left[ {{K_1}{f_1}(t) + {K_2}{f_2}(1)} \right]={K_1}L\left[ {{f_1}(t} \right] + {K_2}L\left[ {{F_2}(t} \right]\]

\[={K_1}{F_1}(s) + {K_2}{f_2}(s)...................................................\left( {24.20} \right)\]

Integration

If a function \[f\left( t \right)\]  is continuous, then the Laplace transform of its integral \[\int {f\left( t \right)} \,\,dt\]  is given by

\[L\left[ {\int\limits_0^t {f\left( t \right)} \,dt} \right]={1 \over s}F\left( s \right)...................................................\left( {24.21} \right)\]

By definition

\[L\left[ {\int\limits_0^t {f\left( t \right)} \,dt}\right]=\int\limits_0^\infty{}\left[{\int\limits_0^t {f\left( t \right)} \,dt} \right]{e^{ - st}}\,dt...................................................\left( {24.22} \right)\]

Integrating by parts, we get

\[= \left[ {{{{e^{ - st}}} \over {-s}}\int\limits_0^t {f\left( t \right)dt} } \right]_0^\infty+{1 \over s}\int\limits_0^\infty{{e^{ - st}}f} \left( t \right)dt...................................................\left( {24.23} \right)\]

Since, the first term is zero, we have

\[L\left[ {\int\limits_0^t {f\left( t \right)dt} } \right]={1 \over s}L\left[ {f\left( t \right)} \right]={{F\left( s \right)} \over s}...................................................\left( {24.24} \right)\]

Differentiation of Transforms

If the Laplace transform of the function exists, then the derivative of the corresponding transform with respect to s in the frequency domain is equal to its multiplication by t in the time domain.

            i.e. \[L\left[ {tf\left( t \right)} \right]={{ - d} \over {ds}}F\left( s \right)...................................................\left( {24.25} \right)\]

By definition

\[{d \over {ds}}F\left( s \right)={d \over {ds}}\int\limits_0^\infty{f\left( t \right){e^{ - st}}dt} ...................................................\left( {24.26} \right)\]

Since s and t are independent variables, and the limits 0, ∞ are constants not depending on s, we can differentiate partially with respect to s within the integration and then integrate the function obtained with respect to t.

\[{d \over {ds}}F\left( s \right)= d \over {ds}}\int\limits_0^\infty{f\left( t \right){e^{ - st}}dt}\]

\[=\int\limits_0^\infty{f\left( t \right)\left[ { - t{e^{ - st}}} \right]} \,dt\]

\[=-\int\limits_0^\infty{\left\{ {tf\left( t \right)} \right\}} {e^{ - st}}dt=-L\left[ {tf\left( t \right)} \right]\]

Hence \[L\left[ {tf\left( t \right)} \right]={{ - d} \over {ds}}F\left( s \right)...................................................\left( {24.27} \right)\]

Integration of Transforms

If the Laplace transform of the function \[f\left( t \right)\] exists, then the integral of corresponding transform with respect to s in the complex frequency domain is equal to its division by t in the time domain.

\[i.e.\,\,\,\,\,\,L\left[ {{{f\left( t \right)} \over t}} \right]=\int\limits_s^\infty{F\left( s \right)ds} ...................................................\left( {24.28} \right)\]

i.e. \[f\left( t \right) \leftrightarrow F\left( s \right)\]

\[F\left( s \right)=L\left[{f\left({}\right)}\right]=\int\limits_0^\infty{f\left( t \right){e^{-st}}\,dt} ...................................................\left({24.29} \right)\]                

Integrating both sides from s to ∞

\[\int\limits_s^\infty{F\left(s\right)\,ds=\int\limits_s^\infty{}\left[{\int\limits_0^\infty{f\left(t\right){e^{-st}}dt}}\right]} ds...................................................\left( {24.30} \right)\]

By changing the order of integration, we get

\[=\int\limits_0^\infty{f\left( t \right)} \left[ {\int\limits_s^\infty{{e^{ - st}}ds} } \right]dt..................................................\left( {24.31} \right)\]

\[=\int\limits_0^\infty{f\left( t \right)} \left( {{{{e^{ - st}}} \over t}} \right)dt\]

\[=\int\limits_{0t}^\infty{}\left[ {{{f\left( t \right)} \over t}} \right]\,\,{e^{ - st}}\,dt = L\left[ {{{f\left( t \right)} \over t}} \right]..................................................\left( {24.32} \right)\]                                                         

\[\int\limits_0^\infty{F\left( s \right)} ds = L\left[ {{{f\left( t \right)} \over t}} \right]..................................................\left( {24.33} \right)\]

Translation in the time Domain

If the function \[f\left( t \right)\] has the transform F(s), then the Laplace transform of \[f\left( {t - a} \right)\,\,u\left( {t - a} \right)\]  is e^-as F(s).  By definition

\[L\left[ {f\left( {t - a} \right)\,u\left( {t - a} \right)} \right]=\int\limits_0^\infty{\left[ {f\left( {t - a} \right)\,u\left( {t - a} \right)} \right]\,{e^{ - st}}\,\,dt} ..................................................\left( {24.34} \right)\]

Since \[f\left({t - a} \right)\,u\left({t - a}\right)=0 &for\,\,t < a\]

\[=f\left( {t - a} \right)\,\,\,\,\,\,for\,\,t > a\]

\[L\left[ {f\left( {t - a} \right)\,u\left( {t - a} \right)} \right]=\int\limits_0^\infty{f\left( {t - a} \right)\,{e^{ - st}}\,\,dt} ..................................................\left( {24.35} \right)\]

\[Put\,\,t - a\,=\,\tau\,then\,\tau+a=t\]

\[dt=d\tau\]

Therefore, the above becomes

\[L\left[ {f\left( {t - a}\right)\,u\left({t - a} \right)}\right]\int\limits_0^\infty{f\left( t \right){e^{-s\left( {\tau+a} \right)}}} d\tau ..................................................\left( {24.36} \right)\]

\[={e^{-as}}\int\limits_0^\infty{f\left(\tau\right){e^{-ST}}d\tau=} {e^{-as}}F\left(s \right)..................................................\left( {24.37} \right)\]

\[L\left[ {f\left( {t - a} \right)\,\,u\left( {t - a} \right)} \right]={e^{ - as}}F(s)..................................................\left( {24.38} \right)\]

Translation in the time domain corresponds to multiplication by an exponential in the frequency domain.

Translation in the Frequency Domain

If the function \[f\left( t \right)\]  has the transform F(s), then Laplace transform of \[{e^{ - at}}f(t)is\,\,F(s + a)\]

By definition,  \[F\left( s \right)=\int\limits_0^\infty{f\left( t \right)} {e^{ - st}}dt..................................................\left( {24.39} \right)\]

and therefore, \[F\left( {s + a} \right)=\int\limits_0^\infty{f\left( t \right)} {e^{ - (s + a)}}dt..................................................\left( {24.40} \right)\]

\[=\int\limits_0^\infty{{e^{ - at}}f\left( t \right)} {e^{ - st}}dt = L\left[ {{e^{ - at}}f\left( t \right)} \right]..................................................\left( {24.41} \right)\]

\[F(s + a)=L\left[ {{e^{ - at}}f(t)} \right]..................................................\left( {24.42} \right)\]

Similarly, we have

\[L\left[ {{e^{at}}f(t)} \right]=F(s - a)..................................................\left( {24.43} \right)\]

Translation in the frequency domain corresponds to multiplication by an exponential in the time domain.

Scale Changing

The scale change property gives the relationship between and F(s) when the time variable is multiplied by a positive constant.

\[L\left\{ {f\left( {at} \right)} \right\}={1 \over a}F\left( {{s \over a}} \right),a > 0..................................................\left( {24.44} \right)\]

By definition

\[L\left[ {f\left( {at} \right)} \right]=\int\limits_0^\infty{f\left( {at} \right)} {e^{ - st}}dt..................................................\left( {24.45} \right)\]

Put \[at=\tau\]

\[dt={1 \over a}d\tau\]

\[L\left[ {f\left( {at} \right)} \right]=\int\limits_0^\infty{f\left(\tau\right)} {e^{{s \over a}\tau}}.{1 \over a}d\tau\]

\[={1 \over a}\int\limits_0^\infty{f\left(\tau\right){e^{{s \over a}\tau}}} d\tau\]

\[={1 \over a}F\left( {{s \over a}} \right)..................................................\left( {24.46} \right)\]