Irrigation Engineering

LESSON 7 Flumes

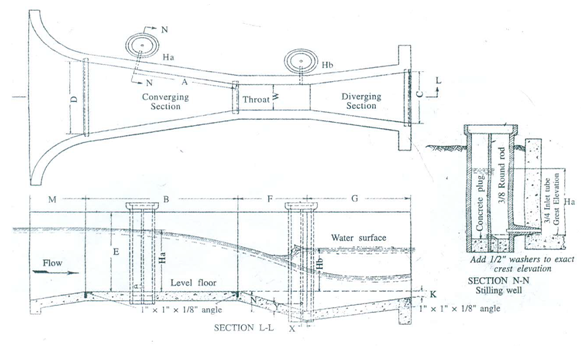
Fig. 7.1.Parshall flume.

(Source: Michael, 2009)

 

Parshall flumes are available in various sizes. Care must be taken whileconstructing the flumes exactly in accordance with structural dimensions.

On the basis of the throat width, Parshall flumes have been classified into three main groups.

a)     Very small - 25.4 mm to 76.2 mm.

b)    Small 152.40 mm to 2438.4 mm.

c)     Large 3048 mm to 15240 mm.

 

Standard dimensions of Parshall flumes with discharge values are presented in Table 7.1 and 7.2, respectively. Discharge through the flume can occur under either free or submerged flow condition. Flow is submerged when the down-stream water elevation retards the rate of discharge. To determine discharge through the flume under free flow condition, head is measured at upstream section (Ha).However, downstream head (Hb) is also measured for submerged flow condition. Free flow condition prevails if the submergence ratio (Hb/Ha) remains within 0.5, 0.6 and 0.7 for width of throat varying from 2.5 to 7.5 cm, 1.5 to 22.5 cm and 3.0 to 24.0 cm, respectively.

 

Table 7.1.Dimensions and capacities of Parshall flume of various sizes (Letter, refer Fig. 7.2)

Throat width	A	B	C	D	E	F	G	K	N	X	Y	Free-flow capacity
cm	cm	cm	cm	cm	cm	cm	cm	cm	cm	cm	cm	Minimum, L s-1	Maximum, L s-1
7.5	31	46	18	26	46	15	30.5	2.5	5.7	2.5	3.8	0.85	28.4
15	41.4	61	39	39.7	61	30.5	61	7.6	12	5.1	7.6	1.4	110.8
23	58.8	86	38	57.5	76	30.5	45.5	7.6	12	5.1	7.6	2.5	253
30	91.5	134	61	84.5	92	61	91.5	7.6	23	5.1	7.6	3.13	456.6

 (Source: Michael, 2009)

 

Table 7.2.Free flow discharge values for Parshall Flume

Discharge, L s-1
Head	Throat width
cm	7.5 cm	15 cm	23 cm	30 cm
3	0.8	1.4	2.6	3.1
4	1.2	2.3	4	4.5
5	1.7	3.3	5.5	7
6	2.3	4.4	7.2	9.6
7	2.7	5.4	8.5	11.4
8	3.4	7.2	11.1	14.4
9	4.3	8.5	13.5	17.7
10	5	10.2	15.9	21.1
11	5.8	11.6	18.1	23.8
12	6.7	13.5	21.1	27.5
13	7.5	15	23.3	31
14	8.5	17.3	26.7	35
15	9.4	19.2	29.5	38.7
16	10.4	21.2	32.5	42.7
17	11.4	23.2	35.6	46.6
18	12.4	25.3	39	51.2
19	13.6	27.8	42.5	55
20	14.3	30	45.8	59.7
21	15.8	32.7	49.3	64.7
22	17.1	35.2	53.3	69.8
23	18.2	37.7	56.8	74
24	19.4	40.1	60.5	79
25	20.7	42.7	64.5	84.1
26	22	45.7	69.3	89
27	23.3	48.1	72.4	94.3
28	24.8	51.5	76.7	100
29	26	54	80.7	105.1
30	27.5	57.3	85.2	111

(Source: Michael, 2009)

 

The discharge is measured by the following formula: 

                                                                                                                                                                     ........(7.1) 

Where, Q is the discharge; C, n are the flume coefficients which vary with the size of the flume and H is the measuring head.

 

Table 7.3 gives a set of standard values for the C,n for different dimensions (these co-efficient are in fps units so the calculated discharge would be in ft³/s and head has to be in ft,)

 

Table 7.3. Value of C and n for different throat widths

Throat width	Coefficient (C)	Exponent (n)
1 in	0.338	1.55
2 in	0.676	1.55
3 in	0.992	1.55
6 in	2.06	1.58
9 in	3.07	1.53
1 ft	3.95	1.55
2 ft	8.00	1.55
3 ft	12.00	1.57
4 ft	16.00	1.58
5 ft	20.00	1.59
6 ft	24.00	1.59
7 ft	28.00	1.60
8 ft	32.00	1.61
10 ft	39.38	1.60
12 ft	46.75	1.60
15 ft	57.81	1.60
20 ft	76.25	1.60
25 ft	94.69	1.60
30 ft	113.13	1.60
40 ft	150.00	1.60
50 ft	186.88	1.60

 (Source:http://www.usbr.gov/pmts/hydraulics_lab/pubs/wmm/chap08_10.htmlaccessed on 16/7/2013)

 

In the above Fig., H_a is upstream head and H_b is downstream head. 

Advantages

a)        This instrument is effective when the total head drop is small.

b)       Its operation is independent of approaching velocity.

c)        Being a self-cleaning device, it is not affected by sand or silt deposition. 

 

7.2 Cut-throat Flume

The geometry of the throat-less flumes with broken plane transition was first developedin Punjab by Harvey in 1912. In the cut throat flume however, theflume discharge and the modular limit are related to the piezometric heads at two pointsin the converging section (h_a) and in the downstream expansion (h_b). One of theadvantages of a cut- throat measuring flumes is that there areonly two walls on each side, resulting in an economic installation. The cross-section canbe rectangular, trapezoidal or triangular, depending only on the availability of appropriate calibration. A U- shaped section can also be used for critical depth flumes.

 

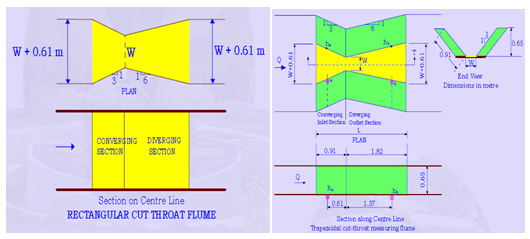
Fig. 7.2.Cut-throat flume. (Source: NPTEL, IIT Madras)

 

Design specifications of a cut-throat flume

L = Total length of the flume,

L₁= Converging section = L/3

L₂=Diverging section= 2L/3,

L_a=Distance to piezometer tap a = 2L/9

L_b=Distance to piezometer tap b= 5L/9

B=width of the converging and diverging section= W + L/4.5

The cut-throat flume can operate either as a free flow or a submerged flow structure. Under free flow conditions, critical depth occurs in the vicinity of minimum width, w, which is called the flume throat or the flume neck. The attainment of critical depth makes it possible to determine the flow rate, knowing only an upstream depth, h_a. The relationship between flow rate Q and upstream depth of flow h_a, in a cut-throat flume under free flow conditions is given by the following experimental relationship: 

       Q = C₁ h_aⁿ L                                  (7.2) 

In which,

Q = flow rate

C₁= free flow coefficient, which is the value of Q when h_a is 1.0 foot.

n = exponent, whose value depends only on the flume length L.

 

 

References

Michael, A.M. (2008). Irrigation Theory and Practice. Vikas Publishing House Pvt.Ltd., New Delhi.

ecourses.vtu.ac.in/nptel/courses/Webcourse.../parshall_flumes.pdf

nptel.iitm.ac.in/courses/IIT-MADRAS/Hydraulics/pdfs/.../13_1b.pdf

http://agriinfo.in/default.aspx?page=topic&superid=8&topicid=64

http://www.alterra.wur.nl/Internet/webdocs/ilri.../pub20-h1.2.pdf

 

Suggested Reading

Michael, A.M. (2008). Irrigation Theory and Practice. Vikas Publishing House Pvt.Ltd, New Delhi.

ecourses.vtu.ac.in/nptel/courses/Webcourse.../parshall_flumes.pdf

nptel.iitm.ac.in/courses/IIT-MADRAS/Hydraulics/pdfs/.../13_1b.pdf

http://agriinfo.in/default.aspx?page=topic&superid=8&topicid=64

http://www.alterra.wur.nl/Internet/webdocs/ilri.../pub20-h1.2.pdf