Reservior & Farm Pond Design

Lesson 23 Stability Analysis IV

The method given below, for determining the factor of safety against the foundation shear, is an approximate method and is based on the assumption that a soil has an equivalent liquid unit weight which would produce the same shear stress as the soil itself.

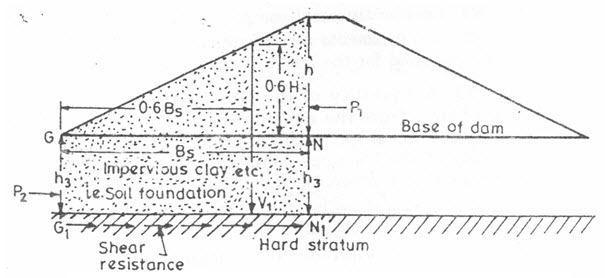
Fig. 23.1. Shear force diagram.

(Source: Garg, 2011)

The total horizontal shear force, under a slope of the dam is equal to the difference between the lateral thrust on a vertical through the top shoulder of the slope and a vertical through the toe of the slope (Fig. 23.1).

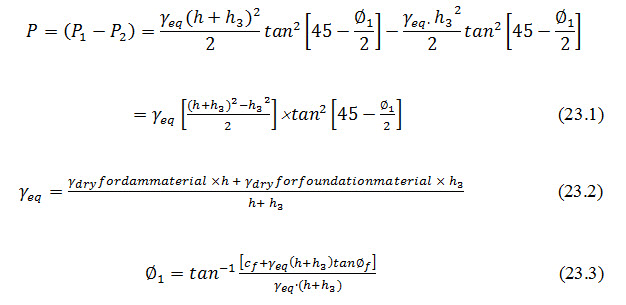
Where, = depth of foundation soil below the dam base, overlying the hard stratum below it, = equivalent unit weight of dry soil in foundation and dam, = equivalent angle of internal friction, and and = unit cohesion and angle of internal friction for the soil in the foundation, respectively. The term  is known as equivalent liquid unit weight.

Now, the average shear stress at the base of the slope

Where, = base width below the slope.

The value of B_s will be equal to Bu for u/s slope and B_d for d/s slope. The minimum value will generate maximum stresses and hence, that particular slope should be considered, which gives the minimum value of . The slope which is less flat and is, therefore the worst slope.

Maximum shear stress has been found by photo-elastic studies to be 1.4 times the average stress and it occurs at a distance of 0.6  from the toe of the slope.

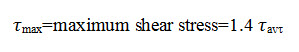
The unit  shear resistance of the foundation soil below the toe at point G₁

Where, is the unit weight of foundation soil and if the average value is given for impervious soils, that value may be used in the equation. But if there is a possibility of foundation soil getting submerged due to large scale seepage that may take place through the foundation soil, then the submerged density may be used in Eqn. 23.5.

Similarly, the unit shear resistance of the soil vertically below the upper point of the considered slope (say at point N₁) is given by

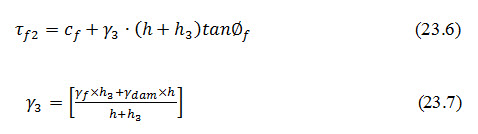
Where, = equivalent unit weight of soil in the dam and foundation at the point N₁, and &= dry densities or submerged densities depending upon the possibilities.

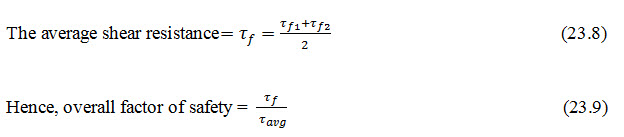
This should be greater than 1.5

The factor of safety (should be greater than unity) at the point of maximum shear (i.e. the point V₁) must also be calculated as follows:

The unit shears resistance at this point V₁

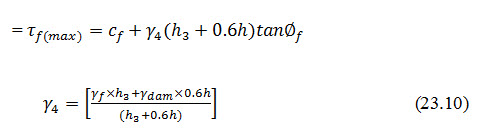
Where, = equivalent weight of soil in dam and foundation

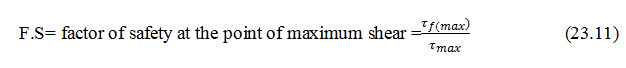
23.2 Seismic Stability of Earth Dam 

An investigation of the stress-strain state of earth-rock dams from the effect of seismic forces is one of the most important problems when designing dams in seismically active regions. Precisely, the behavior of the structure under the effect of seismic forces often determines the design of dams. One of the principal tasks when solving the problem of the seismic effect on an earth-rock dam is the selection of the design characteristics of the soils.

The seismic stability of earth dams is traditionally evaluated under the assumption of cylindrical surfaces of failure. In that case, it is assumed that if the dam withstood the design earthquake, then it would withstand such an earthquake a countless number of times. This assumption is preserved on changing to dynamic methods of solving the problem within the frameworks of elasticity theory and, moreover, many authors use this assumption even when taking plastic deformations into account. On the other hand, soil under dynamic loads have pronounced visco-plastic properties, and each seismic action, weak or strong, causes in the soil of the dam and foundation permanent deformations.

As a result, it is important to evaluate not only whether the dam will withstand a particular action but also how many such actions will occur without dangerous consequences for it.

For dams located in the high seismicity zone, the problem not only of the force of the seismic action but also the frequency of recurrence of the latter can be urgent. In that case, a seismic action even of less intensity but recurring often can sometimes prove to be dangerous. Of course, it is necessary to bear in mind that with a decrease of the force of the action, the portion of the deviator of plastic deformation rapidly decreases and under small and frequently recurring actions the soil in the dam body ultimately begins to behave elastically. In that case, the structure ceases to draw nearer to the limit state. The direction of seismic action is of great significance, since in individual zones of the dam the main role can be played by the accumulation of volumetric compressive strains, which leads to strengthening of soil.

Keywords: Shear force, Foundation, Factor of safety, Seismic stability

References

• Garg, S. K. (2011). Irrigation Engineering and Hydraulic Structures. Khanna Publishers.

• Rasskazov, L. N. and   Bestuzheva A. S. (1992). Seismic Stability of Earth Dams,  Hydrotechnical Construction. 26(2): 91-99.

Suggested Readings

• Punmia, B. C., Pande, B. B. L., Jain, A. K. and Jain, A. K. (2009). Irrigation and Water Power Engineering. Laxmi Publication.

• http://www.most.gov.mm/techuni/media/CE_05016_ch5.pdf

• http://www.ferc.gov/industries/hydropower/safety/guidelines/eng-guide/chap4.pdf

• http://osp.mans.edu.eg/tahany/dams1.htm