Watershed Hydrology

Lesson 28 Other Unit Hydrographs

Example 1

The 4-h, distribution graph of catchment of 50 km² area has the following ordinates:

Unit periods (4-h units)	1	2	3	4	5	6
Distribution (percentage)	5	20	40	20	10	5

 

If the catchment has rainfall of 3.5, 2.2, and 1.8 cm in three consecutive 4-h periods, determine the resulting direct runoff hydrograph by assuming the  index for the storm as 0.25 cm/h.

C1	C2	C3	C4 = C3*4	C5 = C2 – C4	C6	C7 = C6/100	C8 = 2.5*C7; 1.2*C7 (lagged by 4h); 0.8*C7 (lagged by 8 h)			C9 = Summation of C8
Time interval	Rainfall	Infiltration loss	Infiltration loss	Effective rainfall	Avg distribution ratio	Avg distribution ratio	Distributed runoff for  rainfall excess of			Runoff
h	cm	cm/h	cm	cm	(percentage)	(decimal)	2.5 cm	1.2 cm	0.8 cm	cm	m3/s
0-4 h	3.5	0.25	1	2.5	5	0.05	0.125			0.125	4.3
4-8 h	2.2	0.25	1	1.2	20	0.2	0.5	0.06		0.56	19.4
8-12 h	1.8	0.25	1	0.8	40	0.4	1	0.24	0.04	1.28	44.4
12-16 h					20	0.2	0.5	0.48	0.16	1.14	39.6
16-20 h					10	0.1	0.25	0.24	0.32	0.81	28.1
20-24 h					5	0.05	0.125	0.12	0.16	0.405	14.1
24-28 h								0.06	0.08	0.14	4.9
28-32 h									0.04	0.04	1.4

 

Answer

 

28.2 Dimensionless Unit Hydrograph

Dimensionless unit hydrographs based on a study of a large number of unit hydrographs. They are also used to facilitate construction of synthetic unit hydrographs. A typical dimensionless unit hydrograph  contains ordinate (Q/Q_p) which is the discharge Q expressed as a ratio to the peak discharge Q_pand the abscissa (t/T_p), which is the time I expressed as a ratio of the time to peak T_p. By definition, Q/Q_p= 1.0 when t/T_p= 1.0.

 

28.3 Instantaneous Unit Hydrograph

Fig 28.1 shows a typical variation of the shape of unit hydrographs for different values of D. As D is reduced, the intensity of rainfall excess being equal to 1/D increases and the unit hydrograph becomes more skewed. A finite unit hydrograph is indicated as the duration D → 0. The limiting case of a unit hydrograph of zero duration is known as instantaneous unit hydrograph(IUH).

 

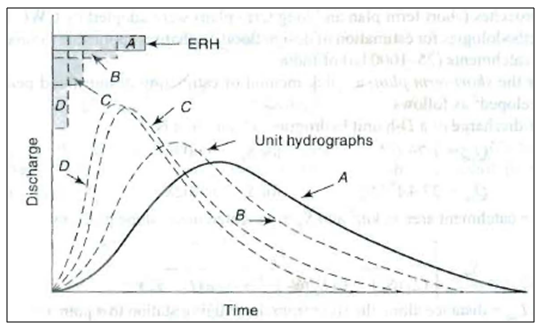
Fig. 28.1.Unit hydrograph of different durations. (Source:Subramanya, 2008)

IUH is a fictitious, conceptual unit hydrograph which represents the surface runoff from the catchment due to an instantaneous precipitation of the rainfall excess volume of 1 cm.

 

IUH is designated as u (t)or sometimes as u(0, t). It is a single-peaked hydrograph with a finite base width and its important properties can be listed as below:

1. 0 ≤ u (t) ≤ a positive value,      for t ˃ 0;
2. u (t) = 0                                   for t ≤ 0;
3. u (t) → = 0                               as t → ∞;
4. = unit depth over the catchment; and
5. Time to the peak time to the centroid of the curve.

The main advantage of IUH is that it is independent of the duration of ERH and thus has one parameter less than a D-h unit hydrograph. This fact and the definition of IUH make it eminently suitable for theoretical analysis of rainfall excess-runoff relationship of a catchment. For a given catchment IUH, being independent of rainfall characteristics, is indicative of the catchment storage characteristics.

 

References

Subramanya, K. (2008). Engineering Hydrology.Third edition, Tata McGraw Hill, 224-237.

 Suggested Reading

Singh, V. P. (1994). Elementary Hydrology.Prentice Hall of India Private Limited,New Delhi.

Suresh R. (2007). Soil and Water Conservation Engineering.Fourth edition, Standard Publishers Distributors, New Delhi.

Murty, V.V.N. and Jha, M.K. (2009).Land and Water Management Engineering.Fifth edition, Kalyani Publishers, Ludhiana.